2018冬令营模拟测试赛(十八)
[Problem A]Table
试题描述


输入
见“试题描述”
输出
见“试题描述”
输入示例
见“试题描述”
输出示例
见“试题描述”
数据规模及约定
见“试题描述”
题解
这题很烦的情况就是最后几步由于贴着下或右边界,只有一种选择,于是与上面的情况不一样,所以考虑枚举有多少步是这样的特殊情况。
下面以最后贴着下边界走的情况为例。
枚举最后 \\(x\\) 格是贴着下边界走的(注意贴着下边界走了 \\(x-1\\) 步),那么我们可以计算出来正常(有向右和向下两种选择的情况)走的步数中,有 \\(n-1\\) 步是向下走的,有 \\(m-x\\) 步是向右走的;于是受路径影响的格子数目就是 \\(2(n-1 + m-x) + x = 2m + 2n - x - 2\\),剩下的 \\(mn - 2m - 2n + x + 2\\) 个格子中每个都有 \\(0 \\sim S\\) 这 \\(S+1\\) 种选择。
不受影响的部分方案数即为
接下来我们还需要计算有多少种路径满足有 \\(n-1\\) 步向下走,\\(m-x\\) 步向右走,这显然是一个组合数,但是注意最后一步一定是向下走,否则贴底的格子就不止 \\(x\\) 个了,所以路径的方案即为
接下来我们需要给路径上每一步确定一个权值,使得这些权值相加恰好等于 \\(S\\),同时需要注意在前面 \\(n-1 + m-x\\) 步中,每走一步都需要比较一下,为了让贪心算法最终走的就是我给它定好的路径,需要满足往下一步时,下方的格子严格大于右方的格子,往右一步时,右方的格子大于等于下方的格子;所以往下走的时候当下方的格子填上 \\(w\\) 时,右方的格子只有 \\(w\\) 种选择,往右走的时候右方的格子填上 \\(w\\) 时,下方的格子有 \\(w+1\\) 中选择。形式化地,这部分的方案数可以表示成下式(我们令 \\(w_i\\) 表示第 \\(i\\) 步走到的格子上的数字)
接下来就是神奇的事情了:上面这一坨可以变成组合数。
先举一个简单的例子,明白这个简单情况后就很容易理解上面那一坨怎么变形了。
就是首先需要在 \\(S+1\\) 个数中选择一个“分界点”,假设选中了分界点是第 \\(p\\) 个元素,那么 \\(x = p-1\\),\\(y = S+1-p\\),即左边的就是 \\(x\\),右边的就是 \\(y\\),那么这样满足了 \\(x+y = S\\),然后由于他要求 \\(xy\\) 的和,由于乘法原理我们知道 \\(xy\\) 等价于左边 \\(x\\) 个元素,右边 \\(y\\) 个元素,从左右分别选一个的方案数;正好,我们在刚刚选好分界点 \\(p\\) 之后左右边分别再选择一个的方案数就是答案了。这就是为什么最终的组合数是从 \\(S+1\\) 个元素中选 \\(3\\) 个。
于是那一坨的式子我们推广一下也可以知道它等于
所以最后 \\(x\\) 格贴着下边界的方案数就是我们上面的东西乘起来
其中 \\(x \\in [2, m]\\)。
最后贴着右边界走的情况不妨留给读者练习。(注意这两种情况不完全对称,不要偷懒直接把 \\(n\\) 和 \\(m\\) 换位置,这样是错的)
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <cassert>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == \'-\') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - \'0\'; c = getchar(); }
return x * f;
}
#define maxn 4000010
#define LL long long
int n, m, S, MOD, fac[maxn], ifac[maxn], Pow[maxn];
int qpow(int a, LL b) {
int ans = 1, t = a;
while(b) {
if(b & 1) ans = (LL)ans * t % MOD;
t = (LL)t * t % MOD; b >>= 1;
}
return ans;
}
int C(int n, int m) {
if(n < m) return 0;
return (LL)fac[n] * ifac[m] % MOD * ifac[n-m] % MOD;
}
int main() {
n = read(); m = read(); S = read(); MOD = read();
int N = max(max(n, m), S) << 2;
ifac[0] = fac[0] = ifac[1] = fac[1] = 1;
rep(i, 2, N) ifac[i] = (LL)(MOD - MOD / i) * ifac[MOD%i] % MOD;
rep(i, 2, N) ifac[i] = (LL)ifac[i] * ifac[i-1] % MOD, fac[i] = (LL)i * fac[i-1] % MOD;
Pow[0] = qpow(S + 1, (LL)n * m);
int invs = qpow(S + 1, MOD - 2);
rep(i, 1, N) Pow[i] = (LL)Pow[i-1] * invs % MOD;
int ans = 0;
rep(x, 2, m) {
ans += (LL)Pow[2*m+2*n-x-2] * C(n - 2 + m - x, n - 2) % MOD * C(S + n + 2 * m - x - 3, 2 * n + 2 * m - x - 4) % MOD;
if(ans >= MOD) ans -= MOD;
}
rep(x, 2, n) {
ans += (LL)Pow[2*m+2*n-x-2] * C(n - x + m - 2, m - 2) % MOD * C(S + n + 2 * m - 4, 2 * n + 2 * m - x - 4) % MOD;
if(ans >= MOD) ans -= MOD;
}
printf("%d\\n", ans);
return 0;
}
[Problem B]Remove
试题描述

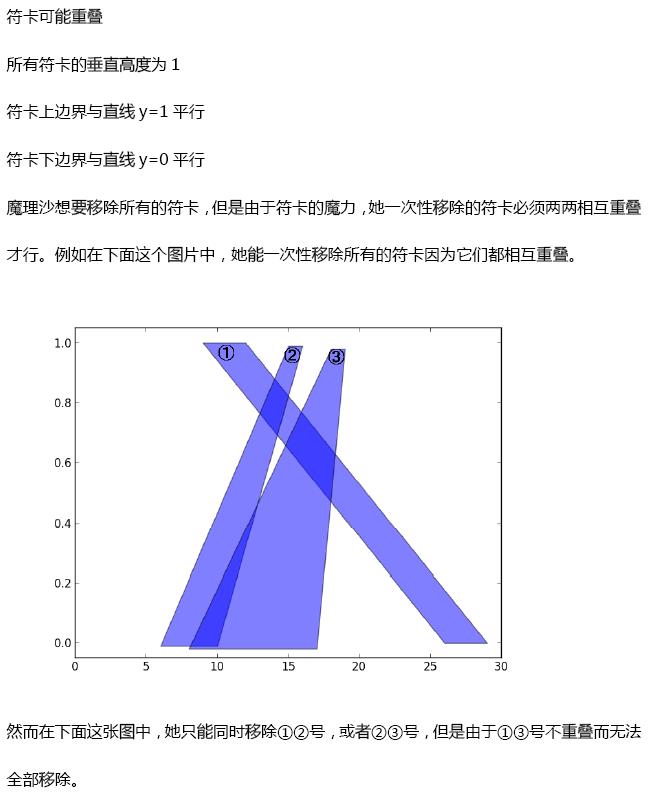
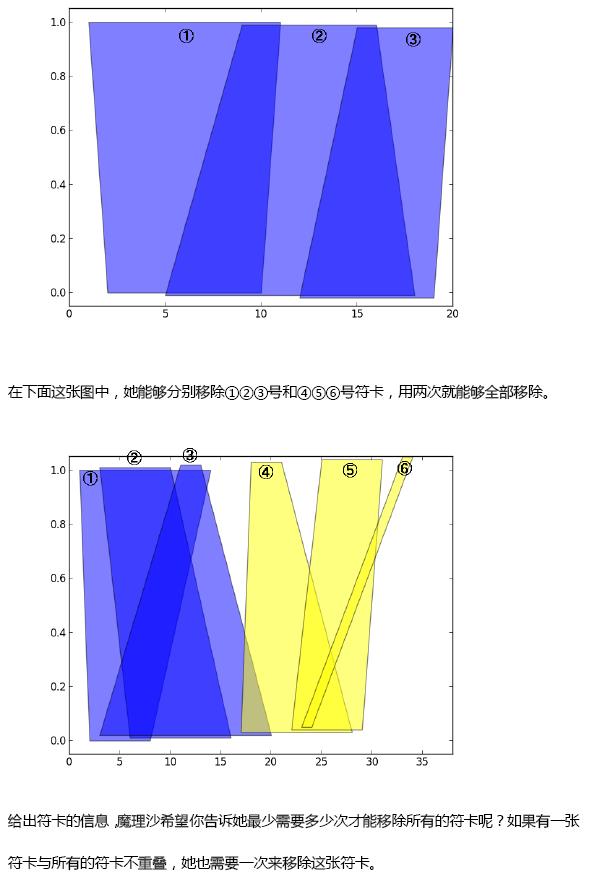


输入
见“试题描述”
输出
见“试题描述”
输入示例
见“试题描述”
输出示例
见“试题描述”
数据规模及约定
见“试题描述”
题解
这题用到了 Dilworth 定理。使用这个定理需要让偏序关系 \\(\\blacktriangleleft\\) 满足如下三个条件
- 自反性:\\(x \\blacktriangleleft x\\) 存在;
- 传递性:若 \\(x \\blacktriangleleft y\\) 和 \\(y \\blacktriangleleft z\\) 存在,则 \\(x \\blacktriangleleft z\\) 存在;
- 反对称性:若 \\(x \\blacktriangleleft y\\) 且 \\(y \\blacktriangleleft x\\) 存在,则 \\(x = y\\)。
令一个四边形 \\(t\\) 的左上、右上、左下、右下角的横坐标分别为 \\(t_{x_1}, t_{x_2}, t_{x_3}, t_{x_4}\\)。
然后这题就是定义四边形 \\(a\\) 和 \\(b\\) 满足偏序关系(即 \\(a \\blacktriangleleft b\\) 存在)当且仅当 \\(a_{x_2} < b_{x_1}\\) 且 \\(a_{x_4} < b_{x_3}\\)(即 \\(a\\) 与 \\(b\\) 无交且 \\(a\\) 在 \\(b\\) 左);同时定义 \\(\\forall a, a \\blacktriangleleft a\\) 存在,可以发现这样定义不会和其他任何限制冲突。
于是这题要求最少反链划分,就可以转化成最长链了。
令 \\(f_i\\) 表示将所有四边形按 \\(x_1\\) 坐标排好序后的以第 \\(i\\) 个四边形结尾的最长链长度(记第 \\(i\\) 个四边形为 \\(g[i]\\)),那么
这样的话每次 dp 出 \\(f_i\\) 之后将它扔到按 \\(x_2\\) 排序的堆里,然后每次转移的时候从堆里拿出 \\(g[j]_{x_2} < g[i]_{x_1}\\) 的所有 \\(j\\),然后在树状数组的 \\(g[j]_{x_4}\\) 位置插入它的 dp 值,然后询问 \\(g[i]_{x_3}\\) 的前缀最小值即可。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <queue>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == \'-\') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - \'0\'; c = getchar(); }
return x * f;
}
#define maxn 100010
int n, num[maxn<<1], cntn, f[maxn];
struct Shape {
int ul, ur, dl, dr;
Shape() {}
Shape(int _1, int _2, int _3, int _4): ul(_1), ur(_2), dl(_3), dr(_4) {}
bool operator < (const Shape& t) const { return ul < t.ul; }
} ss[maxn];
struct cmp {
bool operator () (const int& a, const int& b) const {
return ss[a].ur > ss[b].ur;
}
};
priority_queue <int, vector <int>, cmp> Q;
int C[maxn<<1];
void upd(int x, int v) {
for(; x <= cntn; x += x & -x) C[x] = max(C[x], v);
return ;
}
int qry(int x) {
int res = 0;
for(; x; x -= x & -x) res = max(res, C[x]);
return res;
}
int main() {
n = read();
rep(i, 1, n) {
int ul = read(), ur = read(), dl = read(), dr = read();
ss[i] = Shape(ul, ur, dl, dr);
num[++cntn] = dl; num[++cntn] = dr;
}
sort(ss + 1, ss + n + 1);
sort(num + 1, num + cntn + 1);
cntn = unique(num + 1, num + cntn + 1) - num - 1;
rep(i, 1, n) ss[i].dl = lower_bound(num + 1, num + cntn + 1, ss[i].dl) - num, ss[i].dr = lower_bound(num + 1, num + cntn + 1, ss[i].dr) - num;
int ans = 0;
rep(i, 1, n) {
while(!Q.empty()) {
int u = Q.top();
if(ss[u].ur > ss[i].ul) break;
Q.pop();
upd(ss[u].dr, f[u]);
}
f[i] = qry(ss[i].dl) + 1;
ans = max(ans, f[i]);
Q.push(i);
}
printf("%d\\n", ans);
return 0;
}