数据结构——第六章 图

Posted 2020-10-21 eret9616

 

 

图是由顶点集V和顶点间的关系集合E（边的集合）组成的一种数据结构。可以用二元组定义为：G=（V,E）

 

1. 有向图和无向图：

若用箭头表明了边是有方向性的，则称这样的图为有向图。

否则称为无向图。

 

2.完全图、稠密图、稀疏图

具有n个顶点，n（n-1）/2条边的图，被称为完全无向图，具有n个顶点，n（n-1）条弧的有向图，

称为完全有向图，完全无向图和完全有向图都称为完全图。

 

3.度，入度，出度

在图中，一个顶点依附的边或弧的数目，称为该顶点的度。

对有向图来说，进入或出去。。。的个数被称为入度，出度。

 

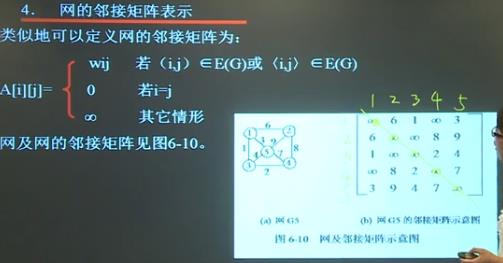
图的邻接矩阵表示

 

 

图的存贮结构

 

图的邻接矩阵表示

1，2，3，4

对应1，2，3，4

看看是否有边。

（先行后列）

 

带权无向图——无向网

 

图的邻接表表示

 

邻接表（出度表）

 

有一些性质。。。因为太多，这里先不介绍了。

 

图的遍历

 

把非线性化化为线性化。

 

 深度优先遍历 （使用栈）

(1)首先访问顶点i,并将其访问标记置为访问过，即visited[i]=1;

(2)然后搜索与顶点i有边相连的下一个顶点j，若j未被访问过，则访问他，并将j的访问标记置为访问过，visited[j]=1，然后从j开始重复这一过程，

若j已访问，再看与i有边相连的其他节点。

(3)若与i有边相连的顶点都被访问过，则退回到前一个访问节点重复刚才的过程，直到图中所有顶点都被访问完为止。

 

 广度优先遍历 （使用队列）

(1)开始时要将其置空

(2)每访问一个顶点，将其入队

(3)在访问一个顶点的所有后继时，要将其出队

(4)若队列为空时，说明每一个访问过的顶点的所有后继均已被访问，因而本次遍历可以结束。若此时还有未访问的顶点，需另选进行遍历。

1进队，1出队，23进队，2出队，45进队...

广度顺序为1，2，3，4，5，6，7，8..

 

生成树和最小生成树

1.生成树

在图论中，常常将树定义为一个无回路连通图，乍一看他似乎不是树，但是但只要选定某个顶点做跟并树根为起点对每条边定向，就可以将它们变为通常的树。

 

3.最小生成树

一般情况下 图中每条边若给定了权，这时我们关心的不是生成树，而是生成树中边上权值之和。若生成树中每条边上权值之和达到最小，称为最小生成树

 

如果不带权，研究生成树。(深度，广度遍历)

如果带有权（带权无向图——无向网），研究最小生成树。

 

普里姆算法和克鲁斯卡尔算法

 

prim算法:

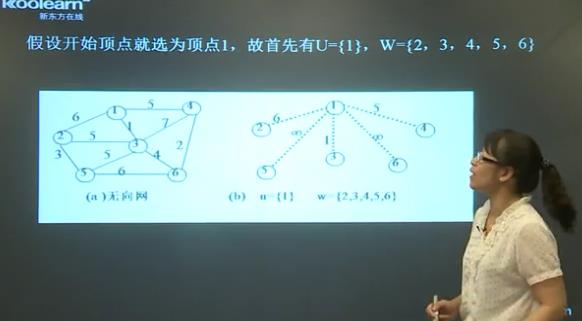
13的权最小(为1)，将13连成实线，将3并入到U集中

现在u是{1,3}  w是{2，4，5，6}

1到2的权是6，3到2的权是5 所以连上3，2...

 

完成图c后进行下一步，从w中继续取一个从u中取一个使权最小，(不能是实线已经连过的)，可以得到，3和6连边是最小的。将6放到u集中，到图d

 

kruskal算法:

克鲁斯卡尔算法的基本思想是:将图中所有边按权值递增顺序排列，依次选定取权值较小的边，但要求后面选取的边不能与前面选取的边构成贿赂，若构成回路则放弃该边，再去选择后面权值较大的边，n个顶点的图中，选够n-1条边即可。

 

1是在13上，13连边，

2是在46上，46连边，

3是在25上，45连边，

4是在36上，36连边，

5有23和35，我们选23连边，

(这个例子写的不好，没有给出原示例的无向网..因为权值都在无向网上面呢)

 

最短路径（有向网，带方向的网）

1.单源点的最短路径

给定一个出发点（单源点）和一个有向网G=（V,E）,求出源点到其他各顶点间的最短路径。

 

 

图(a)带权有向图——有向网

 

迪杰斯特拉算法：

选择源点1,

图(b)

1到各个顶点的权值，1到2最小，连接1和2为实线

1到5 30 1中转2到5 没有，所以1到5还是30

1到3 无穷大，1中转2到3是25，

1到4 无穷大，1中转2到4有8，

图(c)

1到5是30，1到4是11，1到3是28

最小的是1到2到4，连接1到2到4

图(d)

1经2到3是28 1经2到4到3是15

1经2到4到3是23 1直接到3是30

留下最小的，连上34

 

1到5是30，1到4到5是23

1经4到3是15 留下最小的。1经4到3连边

。。。

 

先找最小的，在图a中最小的是1到2，则可以中转的思想来看问题，

 

迪杰斯特拉算法思想:

设置并逐步扩充一个集合S，存放已求出其最短路径的顶点，则尚未确定最短路径的顶点集合是V-S，其中V为网中所有顶点的集合。按最短路径长度递增的顺序逐个以V-S中的顶点加到S中，直到S中包含全部定点，则V-S为空。

 

拓扑排序

 

AOV网  Activity On Vertex Network

在现代化管理中，人们常用有向图来描述和分析一项工程的计划和实施过程，一个工程常被分为多个小的子工程，这些子工程被称为活动（Activity)，在有向图中若以顶点表示活动，有向边表示活动之间的先后关系，这样的图简称为AOV网。

AOE网 Activity On Edge Network

在现代化管理中，人们常用有向图来描述和分析一项工程的计划和实施过程，一个工程常被分为多个小的子工程，这些子工程被称为活动（Activity)，在带权有向图中若以顶点表示事件，有向边表示活动，边上的权值表示该活动持续的时间，这样的图简称为AOE网。

 

 

这些课程有先修后修的制约关系。可以使用拓扑排序来优化。

 

拓扑排序:

1在AOV网中选择一个入度为0的顶点输出它

2.从AOV网中删除此顶点及该顶点发出的所有有向边

重复1，2，直到AOV网中所有顶点都被输出或网中不存在入度为0的顶点。

 

 

 

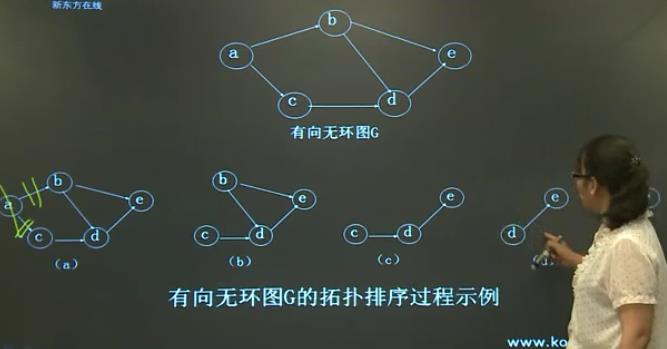
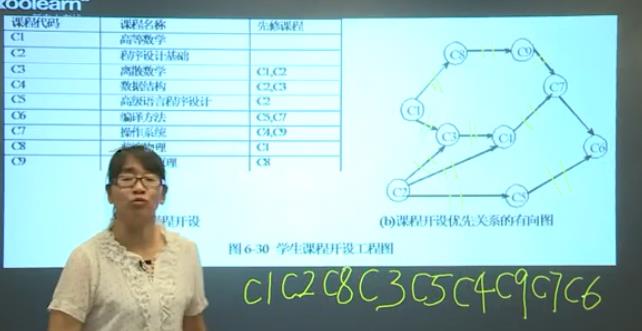
AOV网中不能出现回路（有向环）

 

活动之间互相牵制会导致工程无法按工期去完成。

 

怎么保证关键的活动要干快点，防止某个人慢而导致工期的延误，需要确定关键路径。

 

关键路径

 对AOE网主要研究的问题

 

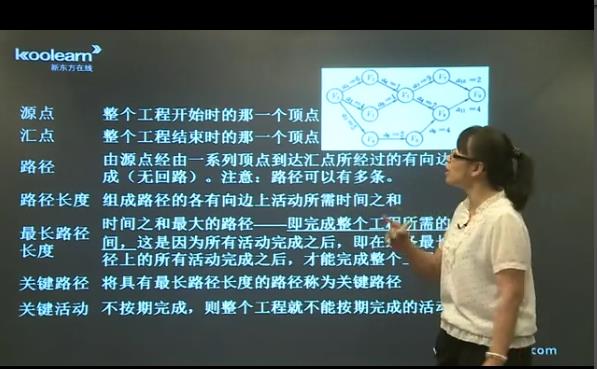
解决两个问题：

1.整个工程最少多少天完成？

2.哪些活动是关键活动？

用i，j表示事件，

对事件有两个， 对活动有三个，如上图

 

 算法

其实就是找最大的那个

 。。。

感觉好像不是特别难理解，但是讲的贼多。就到这里吧。。