数据结构-二叉搜索树

Posted 2020-10-20 RONGWEIJUN

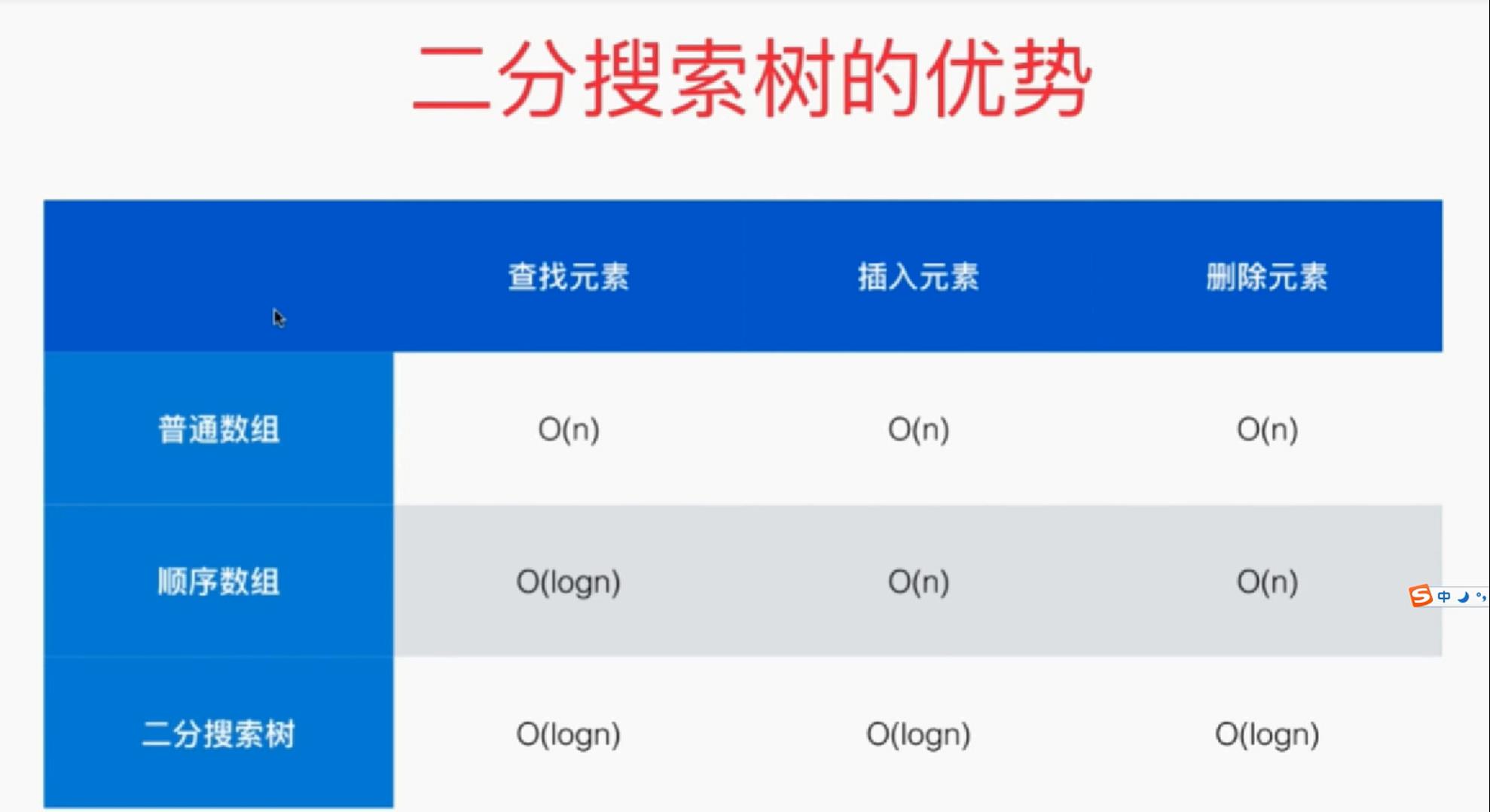
基本定义代码：

        private Node root;
        int count;
        IComparer<Key> comparer;//比较器
        public BST()
        {
            count = 0;
            root = null;
            this.comparer = (comparer == null) ? Comparer<Key>.Default : comparer;
 
        }
        private class Node
        {
            public Key key; //键
            public Value val; //值
            public Node left, right; //指向子树的链接
            public Node(Key key, Value val)
            {
                this.key = key;
                this.val = val;
            }
        }

 

 

 

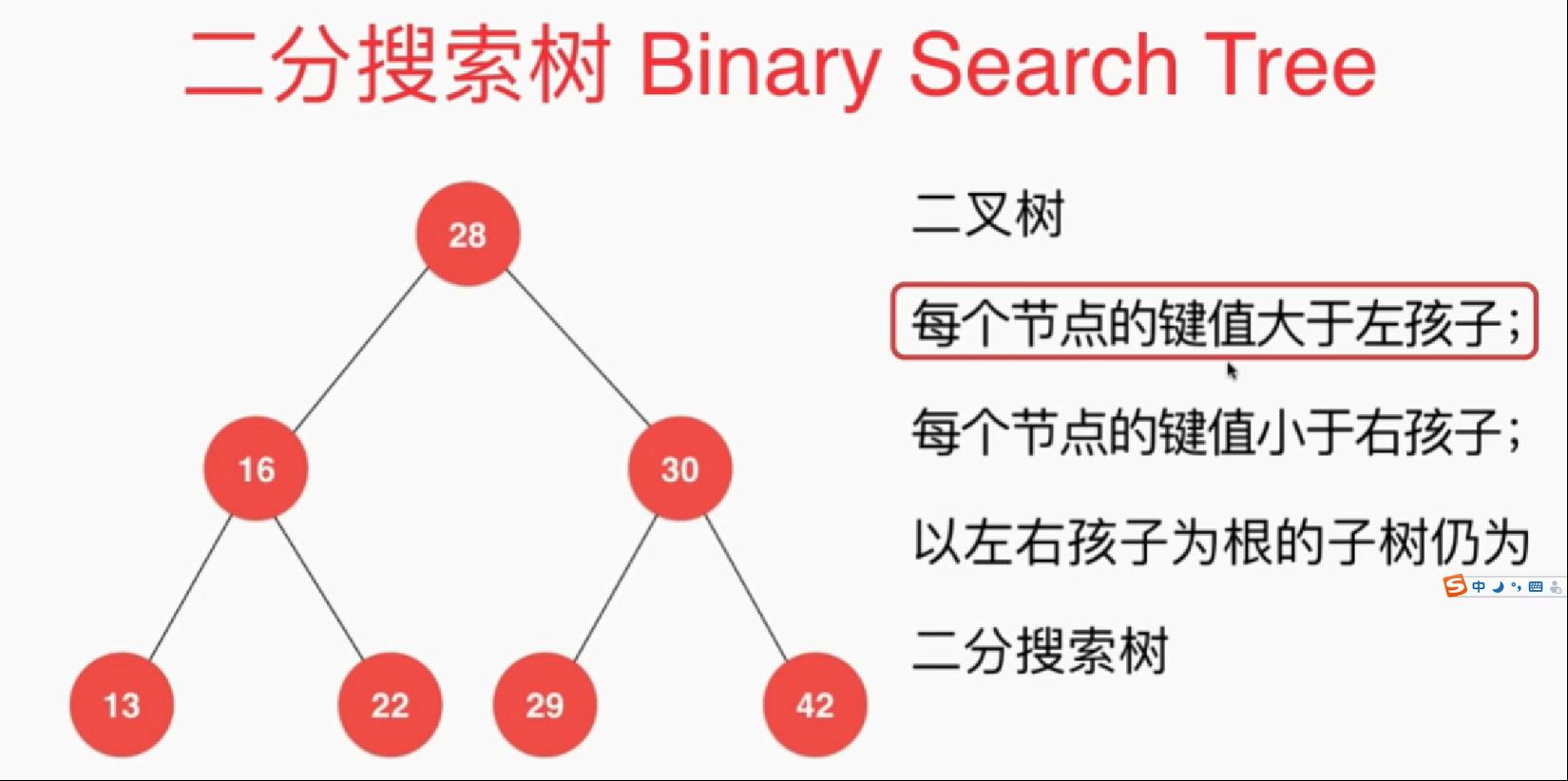
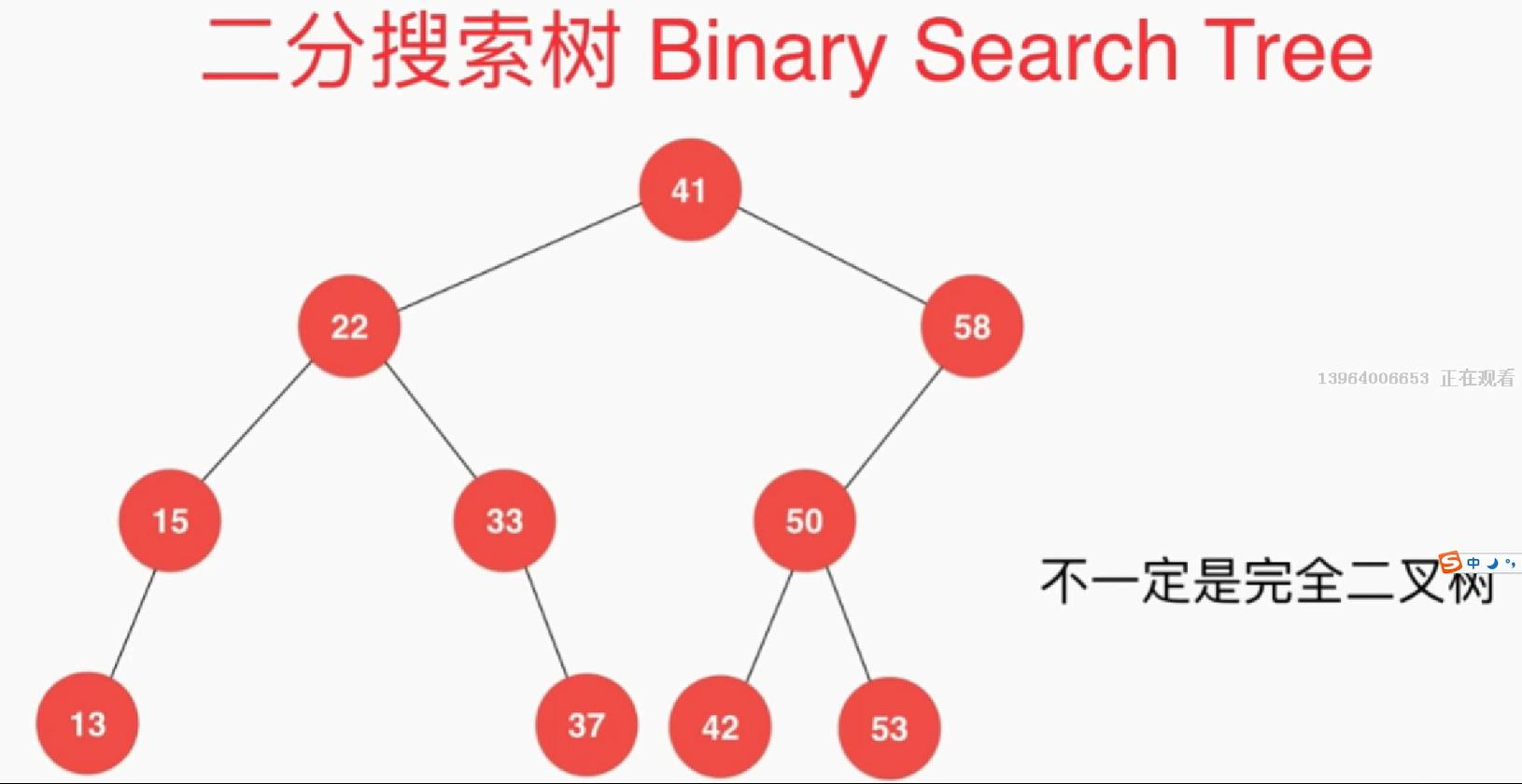
插入实现：

    public void insert(Key key,Value value)
        {
            root = insert(root,key,value);
        }
        // 向以node为根的二分搜索树中, 插入节点(key, value), 使用递归算法
        // 返回插入新节点后的二分搜索树的根
        private Node insert(Node node,Key key,Value value)
        {
            if(node==null)
            {
                count++;
                return new Node(key, value);
            }
            //如果key存在于x为根节点的子树中则更新它的值
            //否则将以key和val为键值对的新结点插入到该子树中
            int cmp = comparer.Compare(key, node.key);
            if (cmp == 0)
                node.val = value;
            else if (cmp < 0)
                node.left = insert(node.left, key, value);
            else
                node.right = insert(node.right, key, value);

            return node;
        }

搜索实现：

        // 查看二分搜索树中是否存在键key
        bool contain(Key key)
        {
            return contain(root, key);
        }
        private bool contain(Node node, Key key)
        {
            //在以x为根节点的子树中 查找并返回key对应的值
            //如果找不到则返回null
            if (node == null)
                return false;
            int cmp = comparer.Compare(key, node.key);
            if (cmp == 0)
                return true;
            else if (cmp > 0)
                return contain(node.right, key);
            else
                return contain(node.left, key);
        }

        // 在二分搜索树中搜索键key所对应的值。如果这个值不存在, 则返回null
        Value search(Key key)
        {
            return search(root,key);
        }
        private Value search(Node node, Key key)
        {
            if (node == null)
                return default(Value);

            int cmp = comparer.Compare(key, node.key);
            if (cmp == 0)
                return node.val;
            else if (cmp > 0)
                return search(node.right, key);
            else
                return search(node.left, key);
        }

 

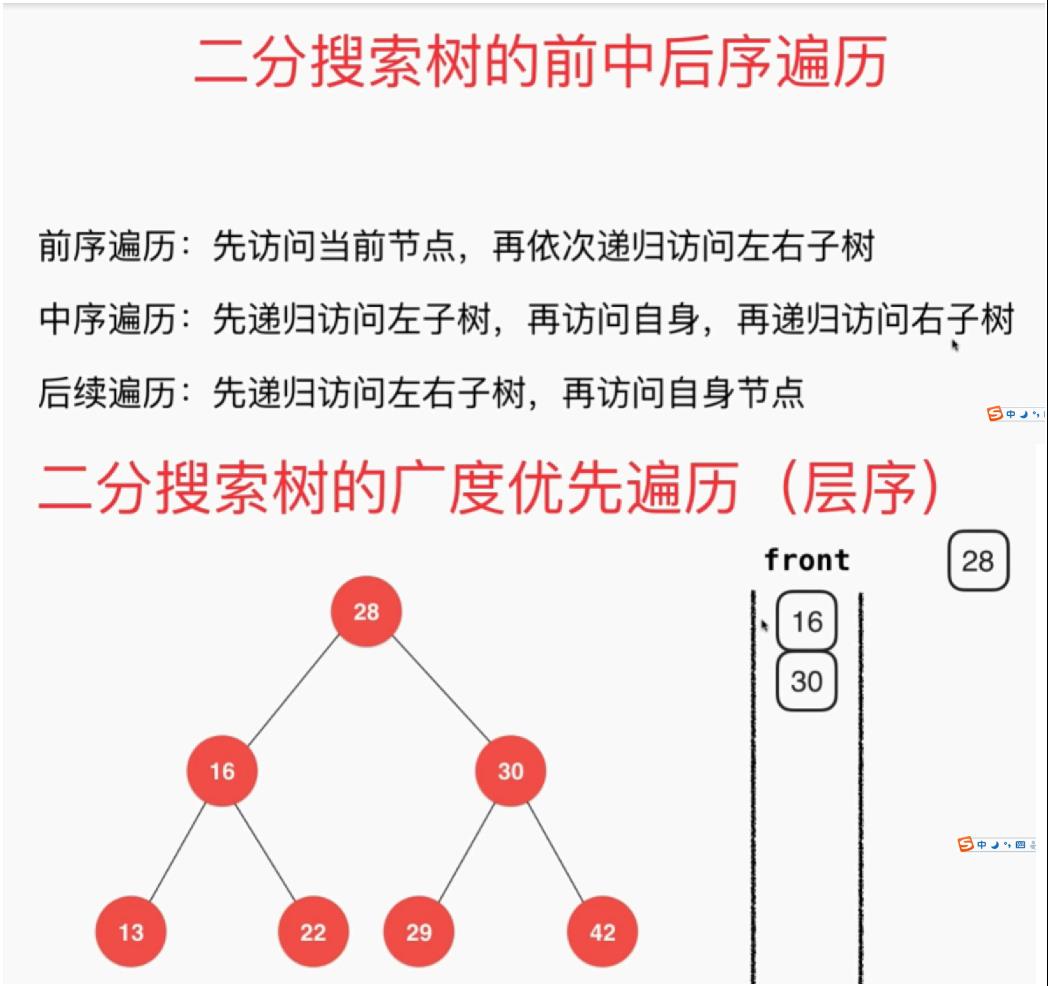
遍历实现：

        //前序遍历
        void preOrder()
        {
            preOrder(root);
        }
        //中序遍历
        void inOrder()
        {
            inOrder(root);
        }
        //后序遍历
        void postOrder()
        {
            postOrder(root);
        }
        //层序遍历
        void levelOrder()
        {
            Queue<Node> q=new Queue<Node>();
            q.Enqueue(root);
            while (q.Count!=0)
            {
                Node node = q.Peek();
                q.Dequeue();
                Console.WriteLine(node.key);
                if (node.left != null)
                    q.Enqueue(node.left);
                if (node.right != null)
                    q.Enqueue(node.right);
            }
        }
        // 对以node为根的二叉搜索树进行前序遍历, 递归算法
        private void inOrder(Node node)
        {
            if (node != null)
            {
                preOrder(node.left);
                Console.WriteLine(node.key);
                preOrder(node.right);
            }
        }
        // 对以node为根的二叉搜索树进行中序遍历, 递归算法
        private void preOrder(Node node)
        {
            if (node != null)
            {
                Console.WriteLine(node.key);
                preOrder(node.left);
                preOrder(node.right);
            }
        }
        // 对以node为根的二叉搜索树进行后序遍历, 递归算法
        private void postOrder(Node node)
        {
            if (node != null)
            {
                preOrder(node.left);
                preOrder(node.right);
                Console.WriteLine(node.key);
            }
        }

 

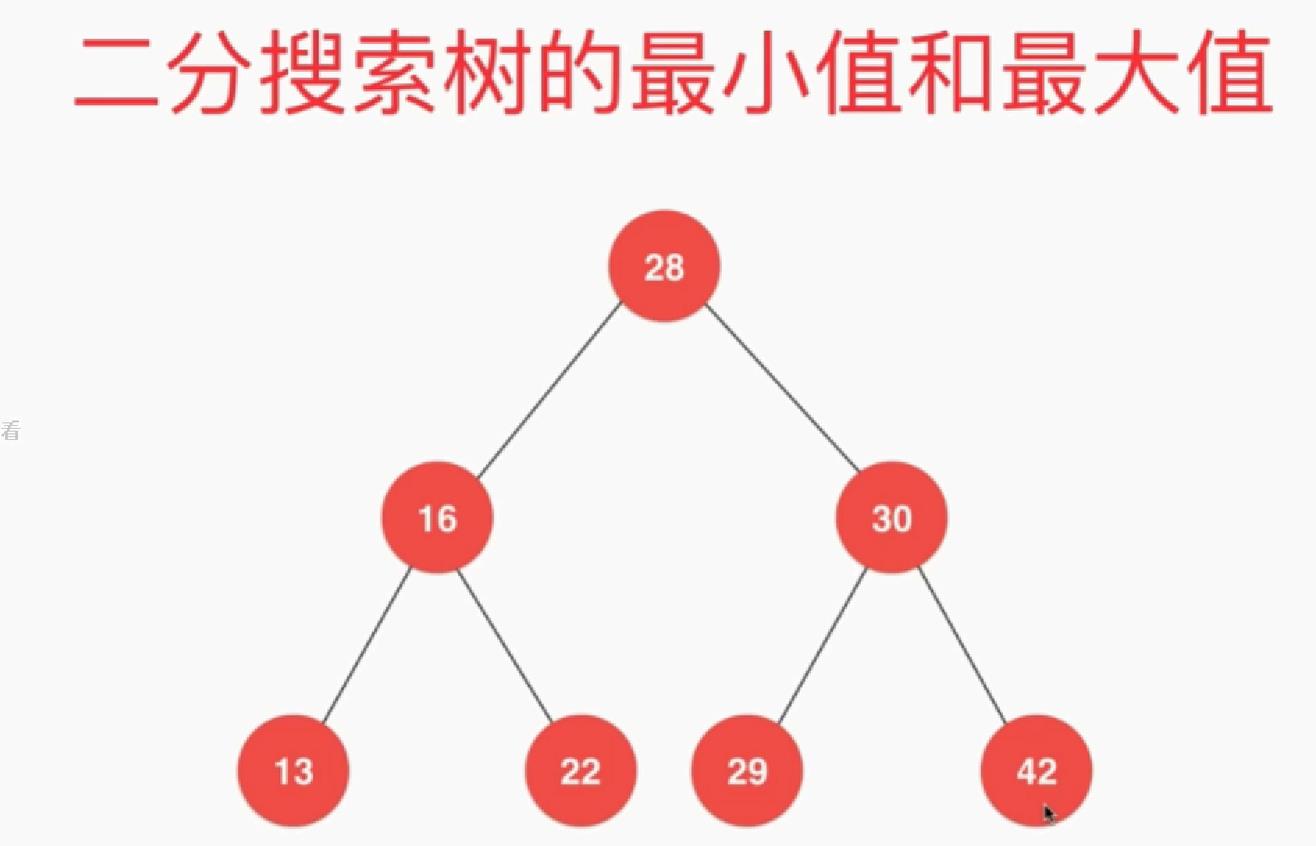
查找最大最小 && 删除最大最小 代码实现:

        //寻找最小得值
        Key miniMum()
        {
            Node minNode = miniMum(root);
            return minNode.key;
        }
        //寻找最大得值
        Key maxiMum()
        {
            Node maxNode = maxiMum(root);
            return maxNode.key;
        }

        // 返回以node为根的二分搜索树的最大键值所在的节点
        private Node maxiMum(Node node)
        {
            if (node.right== null)
                return node;
            return maxiMum(node.right);
        }

        // 返回以node为根的二分搜索树的最小键值所在的节点
        private Node miniMum(Node node)
        {
            if (node.left == null)
                return node;
            return miniMum(node.left);
        }

        //从二叉树中删除最小值所在节点
        void removeMin()
        {
            if (root != null)
                root = removeMin(root);
        }
        //从二叉树中删除最大值所在节点
        void removeMax()
        {
            if (root != null)
                root = removeMax(root);
        }

        // 删除掉以node为根的二分搜索树中的最大节点
        // 返回删除节点后新的二分搜索树的根
        private Node removeMax(Node node)
        {
            if (node.right == null)
            {
                count--;
                return node.left;
            }
            node.right = removeMax(node.right);
            return node;
        }

        // 删除掉以node为根的二分搜索树中的最小节点
        // 返回删除节点后新的二分搜索树的根
        private Node removeMin(Node node)
        {
            if (node.left == null)
            {
                count--;
                return node.right;
            }
            node.left= removeMin(node.left);
            return node;
        }

 

 

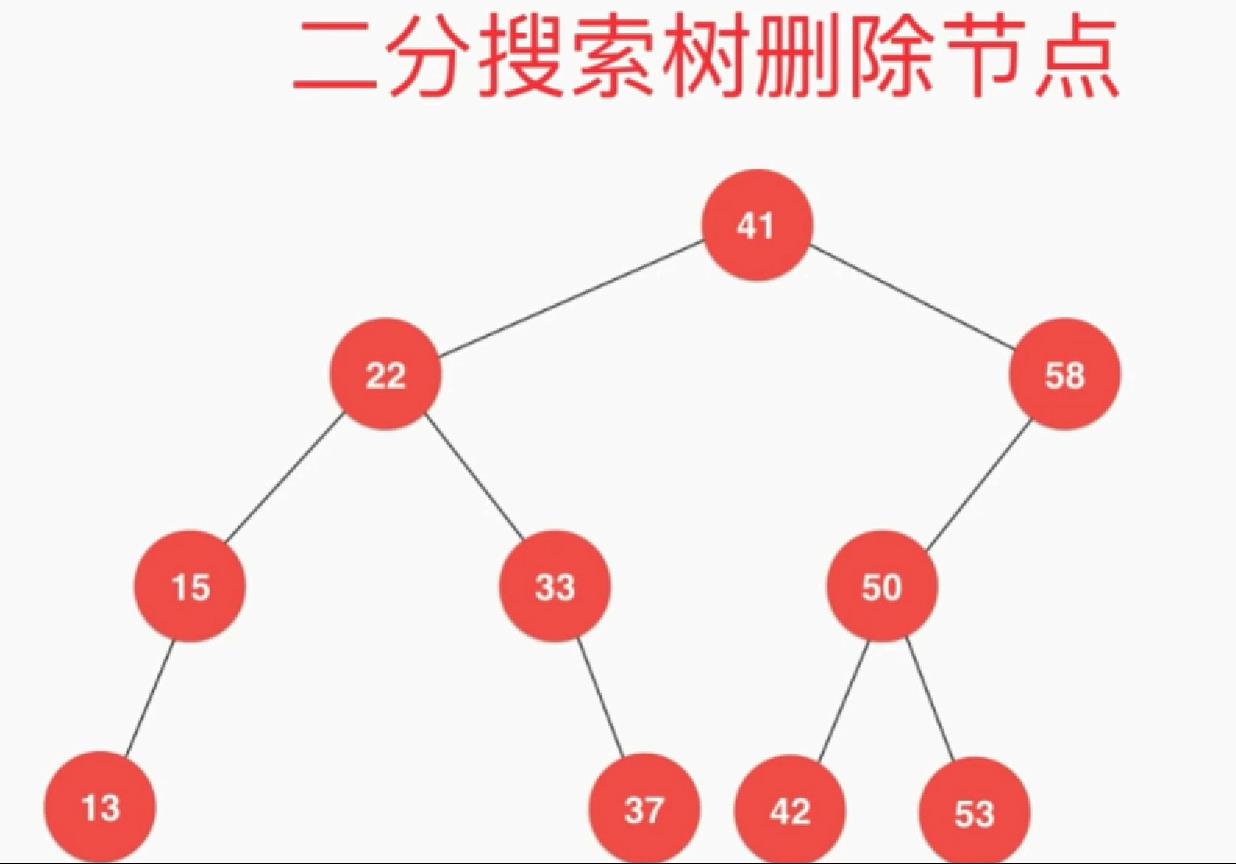
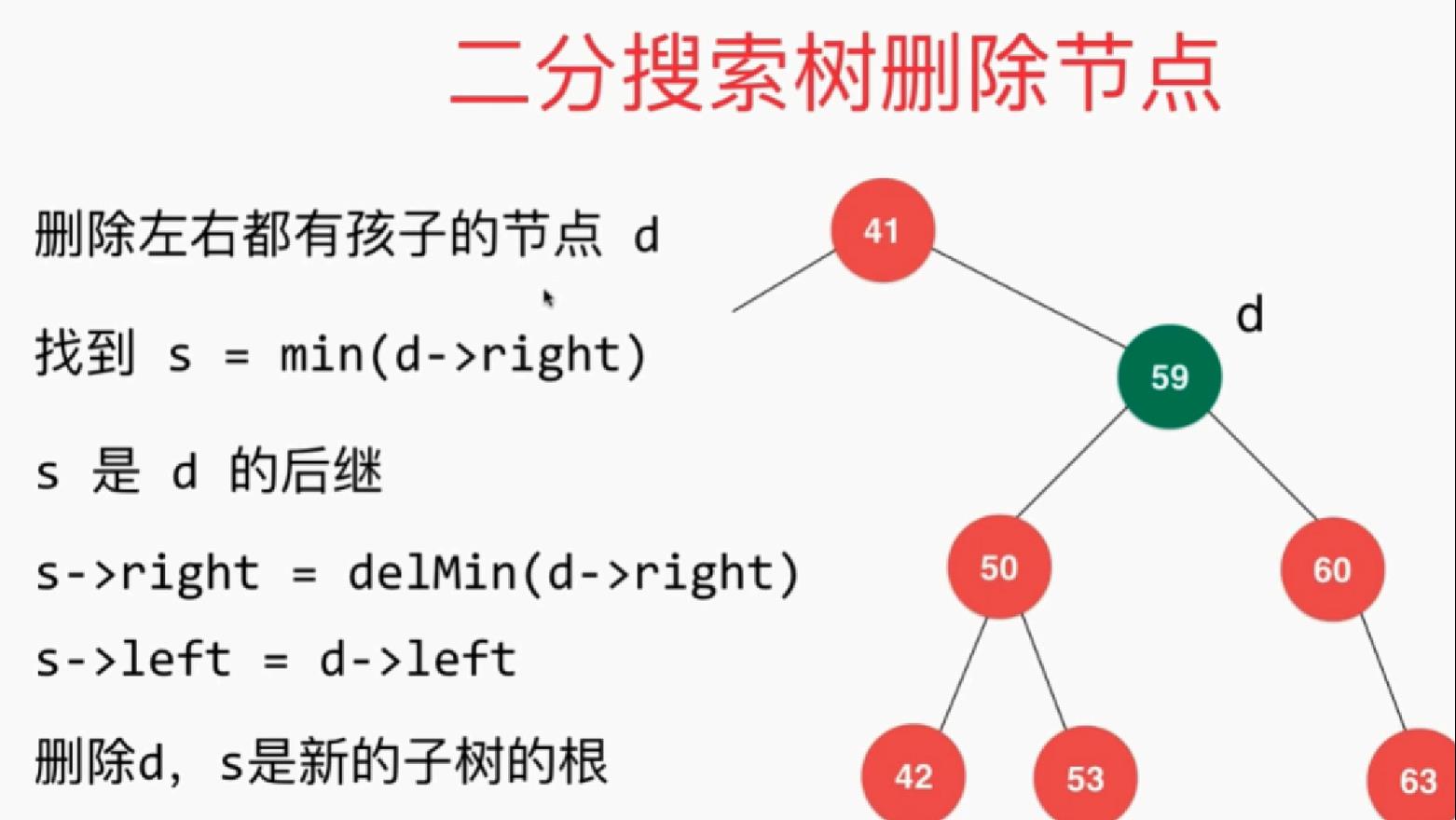
 删除节点实现：

   // 从二分搜索树中删除键值为key的节点
        void remove(Key key)
        {
            root= remove(root,key);
        }

        // 删除掉以node为根的二分搜索树中键值为key的节点, 递归算法
        // 返回删除节点后新的二分搜索树的根
        private Node remove(Node node, Key key)
        {
            //没找到相应得元素
            if (node == null)
                return null;

            int cmp = comparer.Compare(key, node.key);
            if (cmp < 0)
            {
               node.left= remove(node.left, key);
            }
            else if (cmp > 0)
            {
              node.right=remove(node.right,key);

            }
            else  //key==node.key
            {
                // 待删除节点左子树为空的情况
                if (node.left==null)
                {
　　　　　　　　　　　　count--;
                    return node.right;
                }
                // 待删除节点右子树为空的情况
                if (node.right == null)
                {
　　　　　　　　　　　　count--;
                    return node.left;
                }

                //node.left!=null  && node.right!=null
                // 待删除节点左右子树均不为空的情况
                // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
                // 用这个节点顶替待删除节点的位置
                Node DelNode = node;
                node = miniMum(DelNode.right);
                node.right = removeMin(DelNode.right);
                node.left = DelNode.left;
            }
            count--;
            return node;
        }