基于最大堆实现最大优先队列代码
Posted XJX
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于最大堆实现最大优先队列代码相关的知识,希望对你有一定的参考价值。
这个没啥好说的,写完上一个正好写一下这一个,都是基于堆实现的,不过这里没有用C++内置数组,原因是添加删除元素有点麻烦,所以用了vector来实现。
详细内容见《算法导论》P90
----------------------------------------------------代码-----------------------------------------------------------
1 // 基于最大堆实现最大优先队列.cpp: 定义控制台应用程序的入口点。 2 // 3 4 #include "stdafx.h" 5 #include <iostream> 6 #include <vector> 7 8 using namespace std; 9 10 int PARENT(int i); 11 int LEFT(int i); 12 int RIGHT(int i); 13 int MAX_HEAPIFY(vector<int>& A, int i); 14 15 class PriorityQueue //优先队列 16 { 17 protected: 18 vector<int> Queue; 19 public: 20 void push(int x) 21 { 22 Queue.push_back(x); 23 MAX_HEAPIFY(Queue, 0); 24 print(); 25 } 26 int pop() 27 { 28 if (Queue.size() > 0) 29 { 30 int top = Queue[0]; 31 Queue[0] = Queue[Queue.size() - 1]; 32 Queue.pop_back(); 33 MAX_HEAPIFY(Queue, 0); 34 print(); 35 return top; 36 } 37 else 38 { 39 cout << "队列为空!" << endl; 40 return 0; 41 } 42 } 43 int getTop() 44 { 45 if (Queue.size() > 0) 46 { 47 return Queue[0]; 48 } 49 } 50 void set_key(int i,int key) 51 { 52 Queue[i] = key; 53 MAX_HEAPIFY(Queue, 0); 54 print(); 55 } 56 void print() 57 { 58 for (auto c : Queue) 59 cout << c << ends; 60 cout << endl; 61 } 62 }; 63 64 //-------------------------------------------------------------- 65 66 int PARENT(int i) 67 { 68 return (i - 1) / 2; 69 } 70 71 int LEFT(int i) 72 { 73 return 2 * i + 1; 74 } 75 76 int RIGHT(int i) 77 { 78 return 2 * i + 2; 79 } 80 81 //维护最大堆,时间复杂度为O(lgn) 82 int MAX_HEAPIFY(vector<int>& A, int i) 83 { 84 int l, r, largest;//l为左孩子的下标,r为右孩子的下标,largest为三者中最大数的下标 85 int temp; 86 l = LEFT(i); 87 r = RIGHT(i); 88 if (l < A.size() && A[l] > A[i]) 89 largest = l; 90 else 91 largest = i; 92 93 if (r < A.size() && A[r] > A[largest]) 94 largest = r; 95 96 if (largest != i) 97 { 98 temp = A[i]; 99 A[i] = A[largest]; 100 A[largest] = temp; 101 MAX_HEAPIFY(A, largest); 102 } 103 else 104 { 105 if (l >= A.size() && r >= A.size())//到达了叶节点,停止递归 106 { 107 return 0; 108 } 109 MAX_HEAPIFY(A, l); 110 MAX_HEAPIFY(A, r); 111 } 112 } 113 114 115 int main() 116 { 117 PriorityQueue p; 118 p.push(4); 119 p.push(1); 120 p.push(3); 121 p.push(2); 122 p.push(16); 123 p.push(9); 124 p.push(10); 125 p.push(14); 126 p.push(8); 127 p.push(7); 128 cout << endl; 129 for (int i = 0; i < 10; i++) 130 p.pop(); 131 return 0; 132 }
运行结果如下: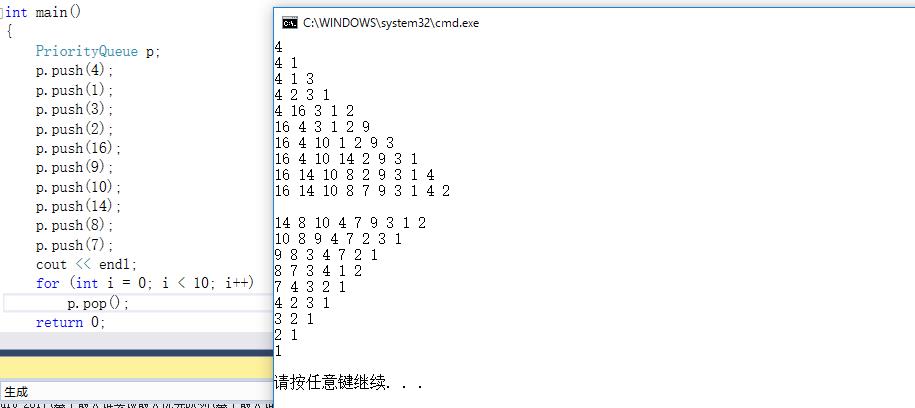
以上是关于基于最大堆实现最大优先队列代码的主要内容,如果未能解决你的问题,请参考以下文章