最大联通子数组

Posted 2020-07-05 linumy

题目:

    返回一个二维整数数组中最大联通子数组的和。

要求：

   1. 输入一个二维整形数组，数组里有正数也有负数。 求所有子数组的和的最大值。要求时间复杂度为O(n)。    

   2.程序要使用的数组放在一个叫 input.txt 的文件中， 文件格式是: 数组的行数, 数组的列数, 每一行的元素， (用逗号分开) 每一个数字都是有符号32位整数，当然，行数和列数都是正整数。

设计思想：

      矩阵中的数是随机生成的，可能会有正有负，所以要首先判断二维数组中哪些位置上的数是正数，利用另一个二维数组记录正数的位置，然后判断哪些数是连通的，我的思路是先判断两个数的行数（列数）是否相同，如果相同，再判断列数（行数）是否相邻，如果相邻即证明两个数连通，计算每个连通块的数值的和，然后再连通不同的块，计算其和，最后比较其中的最大值，即为二维整数数组中最大联通子数组的和。

源程序代码：

#include<iostream>
#include<ctime>
using namespace std;
#define M 100
#include<fstream>

int Max(int n, int a[], int *sm, int *mm)
{
    int b[100] = { 0 };
    int i, Ssum = 0, Mmax= 0;
    for (i = 0; i<n; i++)
    {
        if (Ssum<0)
        {
            Ssum = a[i];
        }
        else
        {
            Ssum = Ssum + a[i];
        }
        b[i] = Ssum;
    }
     Mmax = b[0];
    for (i = 0; i<n; i++)
    {
        if ( Mmax<b[i])
        {
             Mmax = b[i];
            *mm = i;
        }
    }
    for (i = *mm; i >= 0; i--)
    {
        if (b[i] == a[i])
        {
            *sm = i;
            break;
        }
    }
    return Mmax;
}
void main()
{
    ofstream outfile;    
    outfile.open("a.txt");                  
    if(!outfile)
    {
        cerr<<"OPEN ERROR!"<<endl;
        exit(0);
    }
    srand((_int32)time(NULL));
    int m, n, i, j, sm, mm, max1;
    int sum, max;
    int line[M], list[M], t[M];
    int STR[M][M], b[M];
    cout << "二维数组的行:";
    cin>>m ;
    outfile<<m<<endl;
    cout << "二维数组的列:";
    cin>>n ;
    outfile<<n<<endl;
    for(i = 0; i <m; i++)
    {
        for (j = 0; j<n; j++)
        {
             STR[i][j]= rand() % 10;
             if (rand() % 2 == 1)
                 STR[i][j]= STR[i][j]*(-1);
             cout<<STR[i][j]<<" ";
             outfile<<STR[i][j]<<" ";
        }
        cout<<endl;
        outfile<<endl;
    }
    for (i = 0; i<m; i++)
    {
        for (j = 0; j<n; j++)
        {
            b[j] = STR[i][j];
        }
        sum = Max(n, b, &sm, &mm);
        line[i] = sm;
        list[i] = mm;
        t[i] = sum;

    }
    max1 = t[0];
    for (i = 0; i + 1<m; i++)
    {
        if (line[i] <= list[i + 1] && list[i] >= line[i + 1])
        {
            max1 =max1+ t[i + 1];
        }
        for (j = line[i]; j<line[i + 1]; j++)
        {
            if (STR[i + 1][j]>0) 
                max1 =max1+ STR[i + 1][j];                 
        }

    }
    cout <<"最大联通子数组之和"<< max1 << endl;
    outfile<<max1;
}

 

运行结果截图：

 

 

 

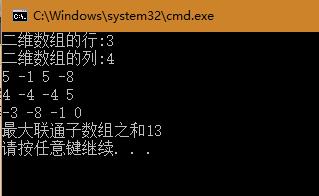
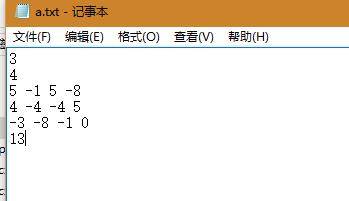
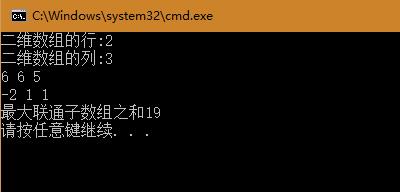
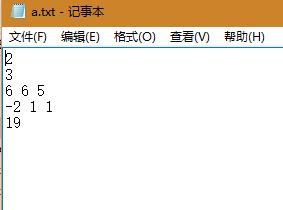
 小组成员：杨涛  http://www.cnblogs.com/GloryYT/