BZOJ3244: [Noi2013]树的计数

Posted 2020-10-20 Blue233333

n<=200000的树，给dfs序和bfs序，问所有可能情况的平均树深。

有点懵的题。。

根据bfs序进行1-n的编号之后，可以通过在bfs序中划层来考察层数。也就是说答案和划层行动的进行的可行度息息相关。所以现在把目光放在数组$x_i$，表示i和i+1(按bfs序重编号后)是否在同一层。

首先，记bfs序中第i个点在dfs序中位置$pos_i$，那么如果$pos_i>pos_{i+1}$，i和i+1一定分层，所以$x_i=1$；其次，如果$pos_i<pos_{i+1}$而$pos_i +1\\neq pos_{i+1}$而i和i+1不同层，说明$pos_i$和$pos_{i+1}$中间一定已经有了和$pos_{i+1}$同层的，那就不可能i+1会紧接在i后面，因此$pos_i<pos_{i+1}$而$pos_i +1\\neq pos_{i+1}$时x_i=0.

剩下的就都是可同层可不同层了吗？并不。还有这种情况：

 

x和x+1强制分层了，如果这时候一z,z<x，他也来搞分层，那图就不能这么画了：

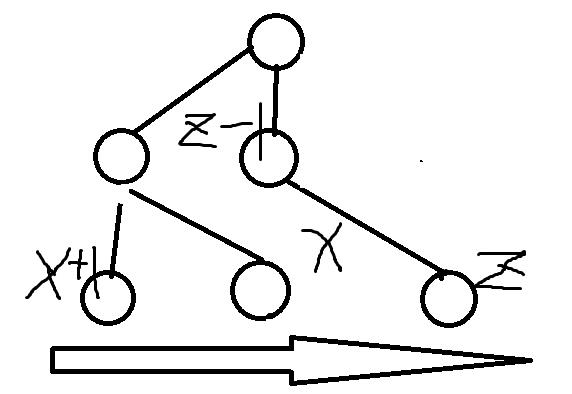
等等，那x+1又得在x下一层。。。怎么可能？

究其原因，是x+1和其父亲在dfs序中满足的一个关系被忽略了：$dep_{a_{i+1}}<=dep_{a_i}+1$。这种关系在x数组中的体现就是：如果$a_i<a_{i+1}$，那么$\\sum_{j=a_i}^{a_{i+1}-1}x_j<=1$。也就是说，这段要有个为1，那其他都是0，可以用差分标记搞一搞。

送个数据

9
1 2 8 9 5 4 6 3 7
1 2 8 5 4 3 9 6 7

 1 #include<string.h>
 2 #include<stdlib.h>
 3 #include<stdio.h>
 4 #include<math.h>
 5 //#include<assert.h>
 6 #include<algorithm>
 7 //#include<iostream>
 8 using namespace std;
 9 
10 int n;
11 #define maxn 200011
12 int a[maxn],b[maxn],pos[maxn],id[maxn],tag[maxn],sum[maxn]; bool diu[maxn];
13 
14 int main()
15 {
16     scanf("%d",&n);
17     for (int i=1,x;i<=n;i++) scanf("%d",&x),b[x]=i;
18     for (int i=1,x;i<=n;i++) scanf("%d",&x),a[b[x]]=i;
19     for (int i=1;i<=n;i++) pos[a[i]]=i;
20     
21     diu[1]=1; sum[1]=1;
22     for (int i=2;i<n;i++) if (pos[i]>pos[i+1]) diu[i]=1;
23     for (int i=2;i<n;i++) sum[i]=diu[i]+sum[i-1];
24     for (int i=1;i<n;i++) if (a[i]<a[i+1] && sum[a[i+1]-1]-sum[a[i]-1]>0) tag[a[i]]++,tag[a[i+1]]--;
25     double ans=1;
26 //    for (int i=1;i<n;i++) cout<<diu[i]<<\' \';cout<<endl;
27     for (int i=1,cnt=0;i<n;i++)
28     {
29         cnt+=tag[i];
30         if (cnt) ans+=diu[i];
31         else ans+=0.5;
32     }
33     printf("%.3lf\\n%.3lf\\n%.3lf\\n",ans-0.001,ans,ans+0.001);
34     return 0;
35 }

View Code