题目描述
如题,给出一个网络图,以及其源点和汇点,每条边已知其最大流量和单位流量费用,求出其网络最大流和在最大流情况下的最小费用。
输入输出格式
输入格式:第一行包含四个正整数N、M、S、T,分别表示点的个数、有向边的个数、源点序号、汇点序号。
接下来M行每行包含四个正整数ui、vi、wi、fi,表示第i条有向边从ui出发,到达vi,边权为wi(即该边最大流量为wi),单位流量的费用为fi。
输出格式:一行,包含两个整数,依次为最大流量和在最大流量情况下的最小费用。
输入输出样例
4 5 4 3
4 2 30 2
4 3 20 3
2 3 20 1
2 1 30 9
1 3 40 5
50 280
说明
时空限制:1000ms,128M
(BYX:最后两个点改成了1200ms)
数据规模:
对于30%的数据:N<=10,M<=10
对于70%的数据:N<=1000,M<=1000
对于100%的数据:N<=5000,M<=50000
样例说明:
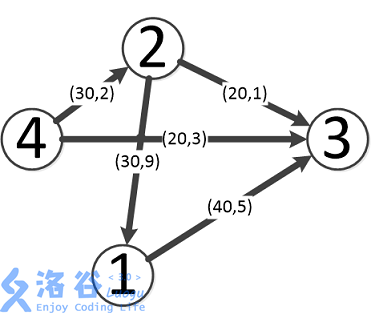
如图,最优方案如下:
第一条流为4-->3,流量为20,费用为3*20=60。
第二条流为4-->2-->3,流量为20,费用为(2+1)*20=60。
第三条流为4-->2-->1-->3,流量为10,费用为(2+9+5)*10=160。
故最大流量为50,在此状况下最小费用为60+60+160=280。
故输出50 280。
Solution:
费用流的模板,关于费用流该怎么算,大家可以去看下别人的博客,我这里也稍微讲一下:
一、求费用流的方法有很多,一般有两条途径:
第一种:先求出最大流,在保证最大流量不变的情况下,调整边的流量使得总费用减少,直到费用无法降低停止。显然,只要网络图中没有负圈(可以画图或想象一下),则当前的流就是最小费用流了。
第二种:每次寻找一条S到T的增广路,这条增广路必须是所有增广路中费用最小的一条,然后不停迭代知道无法增广。显然,此时的流为最小费用流。
二、具体实现:
由于上述的第二种方法是在不停增广,类似于求最大流算法,于是通常我们照此思路求最小费用流,即可转化为求S到T的最短路径问题。
1、费用网络只是在原网络中附加了边的费用cost(e),那么建图时一切照常,只不过对于原有边<u,v>附加费用cost(e),而它的反向边附加费用-cost(e)。
2、建图后,开始增广,注意到增广时只是累加边的费用而边的大小只要大于0就行了,但是因为边权有负值(反向边),所以选用SPFA求最短增广路。
3、因为负边会降低求最短路的效率,所以在每次建立增流网路求得最短路径后,将网络的权值进行一次修正,式再建的增流网络不含负边(要保证最短路径不会因此改变)。修改方法如下:当流量为0,首次建增流网络求最短路时,因为无负边权,所以可以采用标号法。为了使后面建立增流网络时不会出现负边,于是将网络中有流(flow>0)的边权w修改为0。
这样每次增流网络上求得最短路径后,新的边权 W"(u,v)=dis(u)-dis(v)+W(u,v) (dis(u)和dis(v)为新图中x到y的最短路径时u和v的标号值)。首次求最短路时,若(u,v)是增流路径上的边,则由最短路算法必有dis(v)=dis(u)+W‘(u,v)=dis(u)+W(u,v) 将这个式子带入加黑式子有W"(u,v)=0。
若(u,v)不是增流路径上的边,则dis(v)<=dis(u)+W(u,v) 再代入加黑式子,则W"(u,v)>=0。显然,首次修正w后,对于网络中的任意边w都大于等于0,并且有流量的边(增流路径上的边)的w一定等于0。之后的迭代时,若f(u,v)>0,增流网络建立(v,u)边,新的边权W‘(v,u)=-W(u,v)=0,所以不会出现负边了。那么每次迭代都用最开始的加黑的式子去修改边权w,显然对于每一条x到y的路径,它的路径长度都同样增加dis(x)-dis(y)。所以,x到y的最短路径就不会因为对w的修改而发生改变了。
这里有字
我这里用的是用双端队列优化过的SPFA的代码:
1 // luogu-judger-enable-o2 2 #include<bits/stdc++.h> 3 #define il inline 4 using namespace std; 5 bool vis[5005];int dist[5005]; 6 int n,m,s,t,ans=0; 7 int nedge=-1,p[100002],c[100002],cc[100002],nex[100002],head[5005]; 8 il int gi() 9 { 10 int a=0;char x=getchar();bool f=0; 11 while((x<‘0‘||x>‘9‘)&&x!=‘-‘)x=getchar(); 12 if(x==‘-‘)x=getchar(),f=1; 13 while(x>=‘0‘&&x<=‘9‘)a=a*10+x-48,x=getchar(); 14 return f?-a:a; 15 } 16 il void addedge(int x,int y,int z,int zz){ 17 p[++nedge]=y;c[nedge]=z;cc[nedge]=zz;nex[nedge]=head[x];head[x]=nedge; 18 } 19 il bool spfa(int s,int t){ 20 memset(vis,0,sizeof vis); 21 for(int i=0;i<=n;i++)dist[i]=1e9;dist[t]=0;vis[t]=1; 22 deque<int>q;q.push_back(t); 23 while(!q.empty()){ 24 int now=q.front();q.pop_front(); 25 for(int k=head[now];k>-1;k=nex[k])if(c[k^1]&&dist[p[k]]>dist[now]-cc[k]){ 26 dist[p[k]]=dist[now]-cc[k]; 27 if(!vis[p[k]]){ 28 vis[p[k]]=1; 29 if(!q.empty()&&dist[p[k]]<dist[q.front()])q.push_front(p[k]);else q.push_back(p[k]); 30 } 31 } 32 vis[now]=0; 33 } 34 return dist[s]<1e9; 35 } 36 il int dfs(int x,int low){ 37 if(x==t){vis[t]=1;return low;} 38 int used=0,a;vis[x]=1; 39 for(int k=head[x];k>-1;k=nex[k])if(!vis[p[k]]&&c[k]&&dist[x]-cc[k]==dist[p[k]]){ 40 a=dfs(p[k],min(c[k],low-used)); 41 if(a)ans+=a*cc[k],c[k]-=a,c[k^1]+=a,used+=a; 42 if(used==low)break; 43 } 44 return used; 45 } 46 il int costflow(){ 47 int flow=0; 48 while(spfa(s,t)){ 49 vis[t]=1; 50 while(vis[t]){ 51 memset(vis,0,sizeof vis); 52 flow+=dfs(s,1e9); 53 } 54 } 55 return flow; 56 } 57 int main() 58 { 59 memset(nex,-1,sizeof nex);memset(head,-1,sizeof head); 60 n=gi(),m=gi(),s=gi(),t=gi(); 61 int x,y,z,zz; 62 for(int i=1;i<=m;i++){ 63 x=gi(),y=gi(),z=gi(),zz=gi(); 64 addedge(x,y,z,zz);addedge(y,x,0,-zz); 65 } 66 printf("%d ",costflow());printf("%d",ans); 67 return 0; 68 }
提供一种不会被普通SPFA卡极限数据或者zkw卡极限数据的代码(速度不是特别快,关键是稳):
1 // luogu-judger-enable-o2 2 #include <bits/stdc++.h> 3 #define il inline 4 #define debug printf("%d %s\n",__LINE__,__FUNCTION__) 5 using namespace std; 6 const int N=100005,inf=0x3f3f3f3f; 7 int n,m,s,t,cnt=1,h[5005],dis[5005],ans,fee,flow; 8 bool inq[5005],vis[5005]; 9 struct edge{ 10 int to,net,w,c; 11 }e[N]; 12 queue<int> q; 13 il int gi() 14 { 15 int a=0;char x=getchar();bool f=0; 16 while((x<‘0‘||x>‘9‘)&&x!=‘-‘)x=getchar(); 17 if(x==‘-‘)x=getchar(),f=1; 18 while(x>=‘0‘&&x<=‘9‘)a=a*10+x-48,x=getchar(); 19 return f?-a:a; 20 } 21 il void add(int u,int v,int w,int c) 22 { 23 e[++cnt].to=v,e[cnt].net=h[u],e[cnt].c=c,e[cnt].w=w,h[u]=cnt; 24 e[++cnt].to=u,e[cnt].net=h[v],e[cnt].c=-c,e[cnt].w=0,h[v]=cnt; 25 } 26 il bool bfs(int s,int t) 27 { 28 memset(dis,0x3f,sizeof(dis)); 29 memset(inq,0,sizeof(inq)); 30 int x; 31 dis[t]=0; 32 q.push(t); 33 inq[t]=1; 34 while(!q.empty()) 35 { 36 x=q.front(); 37 q.pop(); 38 inq[x]=0; 39 for(int i=h[x];i;i=e[i].net) 40 if(e[i^1].w&&dis[e[i].to]>dis[x]-e[i].c) 41 { 42 dis[e[i].to]=dis[x]-e[i].c; 43 if(inq[e[i].to])continue; 44 inq[e[i].to]=1; 45 q.push(e[i].to); 46 } 47 } 48 return dis[s]<inf; 49 } 50 il int dfs(int u,int flow) 51 { 52 vis[u]=1; 53 if(u==t||flow==0) 54 return flow; 55 int used=0,w; 56 for(int i=h[u];i;i=e[i].net) 57 if(!vis[e[i].to]&&e[i].w&&dis[e[i].to]==dis[u]-e[i].c) 58 { 59 w=dfs(e[i].to,min(e[i].w,flow-used)); 60 e[i].w-=w; 61 e[i^1].w+=w; 62 used+=w; 63 if(used==flow)return used; 64 } 65 return used; 66 } 67 int main() 68 { 69 n=gi(),m=gi(),s=gi(),t=gi(); 70 int u,v,w,c; 71 for(int i=1;i<=m;i++)u=gi(),v=gi(),w=gi(),c=gi(),add(u,v,w,c); 72 while(bfs(s,t)) 73 { 74 vis[t]=1; 75 while(vis[t]) 76 { 77 memset(vis,0,sizeof(vis)); 78 flow=dfs(s,inf); 79 ans+=flow; 80 fee+=flow*dis[s]; 81 } 82 } 83 printf("%d %d",ans,fee); 84 return 0; 85 }