前言
参考资料:
博客:基于LSD的直线提取算法 by tianwaifeimao
致谢
摘要
本文中的LSD算法是一种线段(line segment)检测算法,能够在线性时间内得到亚像素级精度的检测结果。它无需调试参数就可以适用于任何数字图像上,并且能够自行控制误检数量。LSD是一种局部提取直线的算法,速度比Hough要快。但是有局部算法的缺点:
1.对于直线相交情况,因为设置了每个点是否USED,因此每个点只能属于一条直线,若有相交必有至少一条直线被割裂为两条。又因为其基于梯度,直线交点梯度值往往又较小(不被检测为边缘点),因此很有可能相交的两条直线在交点处被割裂为四条线段。
2.由于局部检测算法自增长的特点,对于长线段被遮挡、局部模糊等原因经常割裂为多条直线。这些缺点在Hough变换中不存在。
简介
本文中的LSD算法的目的是检测图像中的局部直线边缘,边缘是灰度值(gray level)从黑到白(或从白到黑)变化明显的图像区域。因此,图像的gradient(梯度)和level-lines是本文中的两个重要概念,如图1所示。
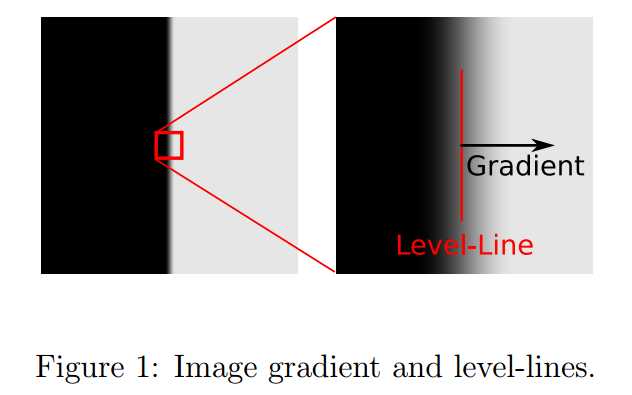
本算法首先计算图像中各个像素点的的level-line角度,从而产生level-line场(一种单位向量场,并且每个向量都同过基准点且相切于level-line)。然后,这个level-line场将在一定容忍角度τ内具有相同的level-line角度的像素划分成不同的像素连通域,这个连通域称之为线段支持域(line support regions),如图2所示。
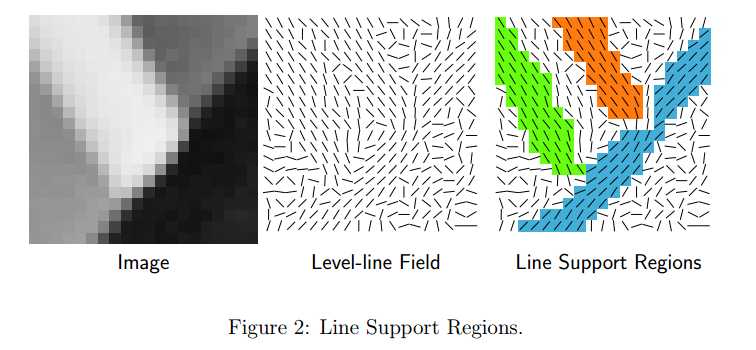
每一个线段支持域都是直线分割的候选区域,并且有个相应的矩形与之一一对应。该矩形的主方向为线段支持域的惯性主轴方向,并且矩形的大小必须覆盖整个线段支持域,如图3所示。

将矩形区域内像素点的level-line角度与矩形主方向角度的夹角在容忍角度τ内的像素点称之为内点(aligned point),如图4所示。统计矩形区域内像素点的数量n和内点的数量k的比值,它们之间的比值将作为判断矩形区域是否为检测的线段的标准,该判断标准是基于一种contrario 方法 和 Helmholtz原则,在本文中我们关心的是矩形域中内点的数量。
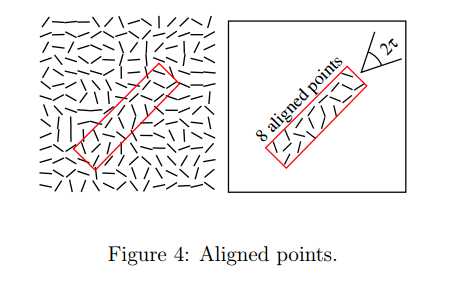
算法
本文中的LSD算法的输入为一张灰度值图像,输出为一系列的检测到的线段(矩形),伪算法如下图所示。

1.以默认 s=0.8的尺度对输入图像进行高斯下采样。
2.计算每一个点的梯度值以及level-line方向(level-line orientation)。
3.根据梯度值对所有点进行伪排序(pseudo-ordered),建立状态列表,所有点设置为UNUSED。
4.将梯度值小于ρ的点状态表中相应位置设置为USED。
5.取出列表中梯度最大(伪排列的首位)的点作为种子点(seed),状态列表中设为USED。
do:
a.以seed为起点,搜索周围UNUSED并且方向在阈值[ -t, t]范围内的点,状态改为USED。
b.生成包含所有满足点的矩形R。
c.判断内点(aligned pt)密度是否满足阈值D,若不满足,截断(cut)R变为多个矩形框,直至满足。
d.计算NFA。
e.改变R使NFA的值更小直至NFA <= ε ,R加入输出列表。
1、图像尺度缩放(Image Scaling)
本文中LSD算法的第一步是将输入图像的尺度缩小至原来的80%,这种尺度缩小的目的是为了减弱甚至消除图像中的锯齿效应(staircase effect)。将图像进行模糊操作也可以带来同样的效果,但是容易检测到图像中的白噪声(white noise)而产生误检。图6显示了两张不同角度的带有离散边缘的图像,这两张图像都有锯齿效应。在原始尺度下使用LSD算法提取线段,左图提取出四根水平线段而不是一整段,右图则没有提取出任何线段。这都不是我们想要的结果。
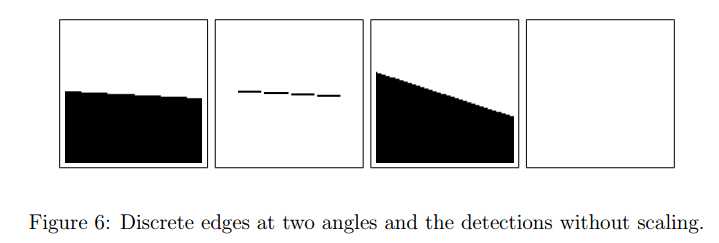
图7中显示了将这两张图像缩放至原来的80%后使用LSD算法的结果,从图中可知,都能提取到边缘并且具有正确的方向(尽管左图中提取的线段是断裂的(fragmented))。

将尺度缩小至原来的80%能够有效的解决锯齿效应(将尺度缩小至80%意味着X轴和Y轴都要缩小至原来的80%,因此图像中像素的数量将减小至原来的64%)。
本文中的图像尺度缩放是通过高斯降采样(Guassian sub-sampling)进行的:图像首先通过高斯核函数(Guassian Kernel)进行滤波从而避免锯齿现象(aliasing),然后进行降采样。高斯核函数的标准差(standard deviation)由σ = Σ/S 决定,这里S 是缩放因子, Σ的值设为0.6,能够很好的避免锯齿效应同时避免图像模糊(image blurring)。
2、梯度计算(Gradient Computation)
图像的梯度是由下图中的2x2的模板(mask)作用于每个点的像素计算到的:
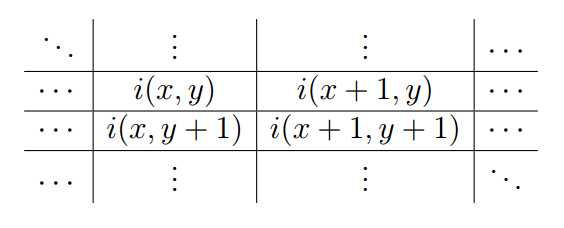
其中i(x, y)代表着坐标为(x, y)的像素点的灰度值,图像的梯度由下列公式计算得到:
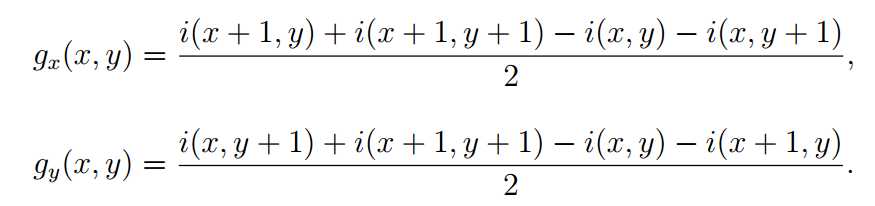
level-line角度由以下公式计算得到:
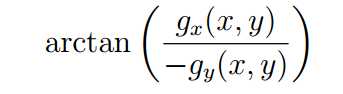
梯度的幅值(magnitude)由以下公式计算得到:
![]()
本算法中选用最小尺寸的模板是为了尽可能的减少梯度计算过程中的彼此依赖。图像的梯度和level-line角度设定(encoder)了边缘的方向,即为从黑到白的转换。值得注意的是,从黑到白和从白到黑的转换是不一样的,两者在梯度和level-line角度都相差了180°。这就意味着LSD算法提取的线段是有方向的并且起点和终点不是随意的(arbitrary)。例如,如果将图像的灰度值反转(revert),那么LSD算法提取出来的线段是一样的,但是线段上的起点和终点将会交换位置 。值得注意的是,本算法计算的图像的梯度值不是像素点(x, y)处的,而是(x+0.5, y+0.5)处的。这个半像素的偏移(offset)会加到输出矩形的坐标中去,从而得到相应的结果。
3、梯度伪排序(Gradient Pseudo-Ordering)
LSD算法是一种贪婪(greedy)算法,像素处理的顺序会对结果产生一定的影响。边缘的像素点往往具有高的梯度值,因此线段的搜索通常从最高的梯度值开始。
排序算法通常需要O(n log n)的时间复杂度,然而一个简单的像素梯度伪排序算法只要求O(n)的线性时间复杂度。为了实现这个目标,我们将像素梯度幅值从0至图像中最大的幅值均匀地分成1024个等级(bin),因此图像中的像素点根据他们的梯度值分成了1024个等级。LSD算法首先使用最大梯度值等级中的像素作为种子像素,然后从第二大梯度值等级的像素中选取种子像素,以此内推直至选完所有的等级。当灰度值范围为[0,255]时,将梯度幅分成1024等分完全够用。
4、梯度阈值(Gradient Threshold)
小梯度值的像素点一般出现在平滑区域或者是梯度变化缓慢的区域。同时,在梯度计算的过程中量化这些点的值会造成很大的误差。在LSD算法中,梯度值小于阈值ρ的像素不能用于线段支持域(line-support regions)和矩形的构建。
假定量化误差为n和存在理想的图像i,我们可以得到:
![]()
根据图8,我们可以得到:

![]()
其中q 是|∇n|的界限(bound)。利用这个准则我们将角度误差大于角度容忍度τ 剔除。假设|角度误差|≤ τ,我们可以得到:
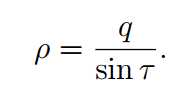
梯度阈值ρ由q和τ 决定,其中q是梯度值计算过程中量化效应产生的可能误差,τ是区域增长算法中用到的角度容忍度。根据经验,我们将q设为2.
5、区域增长(Region Growing)
线段支持域是通过合并相同方向的level-line实现的,依赖一种区域增长算法。通过搜索邻居8点中的未使用像素点来确定是否加去线段支持域中,当level-line角度和区域角度θregion 小于角度容忍度τ时将该level-line添加到线段支持区域中。初始的区域角度是由种子像素的level-line角度确定,然后在区域中每增加一个像素点都会更新一次区域角度,有下列公式确定:
区域增长伪算法如下图所示:

输入:level-line场LLA,种子像素点P,角度容忍度τ和每个像素的状态变量。
输出:一组像素区域
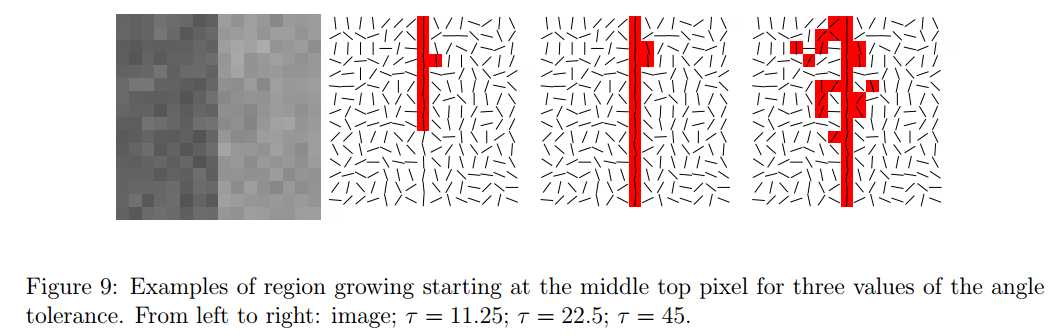
角度容忍度设为22.5度时最为合理,在该容忍度范围内的像素点都会加入到线段支持域中,他们很大程度上和区域的方向保持一致。如下图所示,实验发现,容忍度为22.5是个较好的参数。
6、矩形近似(Rectangular Approximation)
一个线段对应一个矩形,在评估线段支持域前需要找到与之对应的矩形。将线段支持域看成一个刚体,像素点的梯度值作为该点的质量。矩形的中心为线段支持域的质心,矩形的主方向为线段支持域的第一惯性轴方向。矩形的长度和宽度为包含整个线段支持域的最小值。

7、NFA计算(NFA Computation)
NFA:the number of false alarms
The validation step is based on the a contrario approach and the Helmholtz principle proposed by Desolneux。
the Helmholtz principle:在完美噪声图像图像中不应该检测到目标。 contrario approach:一个不会检测到目标的噪声图像。对于本课题,contrario model是一个像素值为level-line angle的图像。其level-line angle随机分解为独立且服从平均分布于[0-2*PI]。这里用NFA(Number of False Alarms)来评判观测图像中某个候选矩形少于contrario model中相同位置矩形里内点的数量的概率,NFA越大,表明当前矩形与contrario model中相同位置越相似,相反的,当前矩形越有可能是“真正的目标”。
其中:
NFA = N * Ph0[ k(r,I) >= k(r,i) ]
上式中,N为当前大小(m*n)图像中直线(矩形框)的数量。在m*n的图像中直线的起点和终点分别有m*n种选择,所以一共有(m*n)*(m*n)种起点和终点搭配。线段的宽度为[0,m*n ^0.5]。因此在m*n大小的图像中有(m*n)^2.5 种不同直线。N=(m*n)^2.5。k(r,I) 为contrario model ,I 中 r 矩形里aligned pt的数量。k(r,i) 为observe img,i 中 r 矩形里aligned pt的数量。
根据contrario model的建立规则,每个像素都服从值域为[0,2*PI]的二项分布。
设k(r,i)=k。
其中:
角度正负容忍误差为t,总容忍误差为2t。那么在contrario model中某个点为aligned pt的概率为 p=2*t / 2*Pi = t / PI。那么,在 I 中的 r 矩形里,总像素个数为 n。I 中的 r 矩形里aligned pt个数k(r,I)大于等于k的话,可选择的值为k(r,i)、k(r,i)+1、k(r,i)......n。概率为: ∑ p^i * (1-p)^(n-i) ,i=k,k+1,k+2……n。
因此:
NFA = (m*n)^2.5 * ∑ p^i * (1-p)^(n-i) ,i=k,k+1,k+2……n
如果NFA的值很大,认为当前事件出现在contrario model的概率很大,将其认为是背景中的一部分。相反的,认为目标是相对突出(rare)的,是一个合适的“直线”。
即:NFA <= ε ε-meaningful rectangles :
E(ho)[ ∑NFA(r) <= ε ] <= ε , r∈ R。R为图像中所有直线的集合。E为期望运算。ho为contrario model。根据论文,ε =1
8、内点密度(Aligned Points Density)

如上图所示,因为t的存在且有正负号容忍范围,容易出现图中线段支持域增长不合理,此时应将矩形截断为两个更小的矩形更为合适。若如图分割的区域包含的直线形成的角为钝角,本次操作只留下包含种子的一段,舍弃另一段。舍弃的点重置为UNUSED。
d = k / n。k为类内点个数,n为R的length*width。若d > D。accepted。否则,需要将矩形截断。在这里设置D=0.7。文章认为这个数字既能保证同一个矩形中的类内点属性相近,也能保证矩形不会被过分的分割为小的矩形。若没满足d > D 分割方法分为“缩小角度容忍阈值”与“缩小区域半径”的方法。缩小角度容忍阈值:简单的将t值缩小,再次从当前R的seed开始搜寻。如果这一步仍为满足d > D,将逐步舍弃离seed较远的点,直至满足不等式未知。类内点的计算将会解决曲线因为t的存在而误识别为直线的状况。
9、矩形改进(Rectangle Improvement)
如果当前的R仍旧不能满足NFA,以下的方法将对其进行改进。考虑到在有些情况下,删除line-support region中的一个点会减少R的 length-1个点(想象为对角线)。对不满足NFA的R,采取以下策略:
1.减小p=p/2
2.短边减少一行
3.长边减少一行
4.长边减少另一行
5.减小p=p/2 直至满足NFA或R过小被拒或p为原来的1/32。