数组各种排序算法和复杂度分析

Posted 2020-10-20 andywu

 

Java排序算法

1）分类：

• 插入排序（直接插入排序、希尔排序）
• 交换排序（冒泡排序、快速排序）
• 选择排序（直接选择排序、堆排序）
• 归并排序
• 分配排序（箱排序、基数排序）

所需辅助空间最多：归并排序

所需辅助空间最少：堆排序

平均速度最快：快速排序

不稳定：快速排序，希尔排序，堆排序。

2）选择排序算法的时候要考虑

• 数据的规模 、

• 数据的类型 、

• 数据已有的顺序。
• 一般来说，当数据规模较小时，应选择直接插入排序或冒泡排序。任何排序算法在数据量小时基本体现不出来差距。 考虑数据的类型，比如如果全部是正整数，那么考虑使用桶排序为最优。  考虑数据已有顺序，快排是一种不稳定的排序（当然可以改进），对于大部分排好的数据，快排会浪费大量不必要的步骤。数据量极小，而起已经基本排好序，冒泡是最佳选择。我们说快排好，是指大量随机数据下，快排效果最理想。而不是所有情况。

3）总结：

——按平均的时间性能来分：   

• 时间复杂度为O(nlogn)的方法有：快速排序、堆排序和归并排序，其中以快速排序为最好；    
• 时间复杂度为O(n2)的有：直接插入排序、起泡排序和简单选择排序，其中以直接插入为最好，特别是对那些对关键字近似有序的记录序列尤为如此；     
• 时间复杂度为O(n)的排序方法只有，基数排序。 当待排记录序列按关键字顺序有序时，直接插入排序和起泡排序能达到O(n)的时间复杂度;而对于快速排序而言，这是最不好的情况，此时的时间性能蜕化为O(n2)，因此是应该尽量避免的情况。简单选择排序、堆排序和归并排序的时间性能不随记录序列中关键字的分布而改变。

——按平均的空间性能来分（指的是排序过程中所需的辅助空间大小）：     

• 所有的简单排序方法(包括：直接插入、起泡和简单选择)和堆排序的空间复杂度为O(1)；
• 快速排序为O(logn )，为栈所需的辅助空间;
• 归并排序所需辅助空间最多，其空间复杂度为O(n );
• 链式基数排序需附设队列首尾指针，则空间复杂度为O(rd )。

——排序方法的稳定性能：

• 稳定的排序方法指的是，对于两个关键字相等的记录，它们在序列中的相对位置，在排序之前和 经过排序之后，没有改变。
• 当对多关键字的记录序列进行LSD方法排序时，必须采用稳定的排序方法。
• 对于不稳定的排序方法，只要能举出一个实例说明即可。
• 快速排序，希尔排序和堆排序是不稳定的排序方法。

各种排序算法Java版

 

/*
 * Copyright (c) 2005-2015 XXX Corporation. All rights reserved.
 *
 * Project Name: test
 * File Name:    SortTest.java
 * Package Name: XXX
 * date:         2016年7月28日
 *
 */
package dt;
import java.util.Arrays;
/**
 * ClassName:   SortTest <br/>
 * Description: TODO ADD DESCRIPTION. <br/>
 * date:        2016年7月28日 上午8:25:39 <br/>
 *
 * @author      danier
 */
public class SortTest {
    static int[] a = { 5,17,16, 7,10, 9, 18,4,15,14, 3, 1, 19,0, 20,6,13, 2, 12,8,11 };
    /**
     * main: ADD DESCRIPTION. <br/>
     * 执行流程: (可选). <br/>
     * 使用方法: (可选). <br/>
     * 注意事项: (可选). <br/>
     *
     * @author danier
     * @param args
     */
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        long begin = System.currentTimeMillis();
        SortTest st = new SortTest();
        st.bubbleSort();
        st.selectSort();
        st.insertSort();
        st.halfInsertSort();
        st.hillsort();
        st.mergeSort(0, a.length - 1);
        st.quickSort(0, a.length - 1);
        long over = System.currentTimeMillis();
        System.out.println("使用的时间为：" + (over - begin) + "毫秒");
        System.out.print(Arrays.toString(st.a));
    }
    //    复杂度分析：一共要比较 ((n-1)+(n-2)+...+3+2+1)=n*(n-1)/2次，所以时间复杂度是O(n^2)
    //    冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较，
    //    交换也发生在这两个元素之间。所以，如果两个元素相等，我想你是不会再无聊地把他们俩交换一下的；
    //    如果两个相等的元素没有相邻，那么即使通过前面的两两交换把两个相邻起来，这时候也不会交换，
    //    所以相同元素的前后顺序并没有改变，所以冒泡排序是一种稳定排序算法。
    public void bubbleSort() {
        for (int i = a.length - 1; i > 1; i--) {
            for (int j = 0; j < i; j++) {
                if (a[j] > a[j + 1]) swap(j, j + 1);
            }
        }
    }
 
    //    选择排序是不稳定算法，最好的情是已经排好顺序，只要比较n*(n-1)/2次即可，
    //    最坏情况是逆序排好的，那么还要移动O(n)次,由于是低阶故而不考虑不难得出选择排序的时间复杂度是O(n^2)
    //    比较拗口，举个例子，序列5 8 5 2 9， 我们知道第一遍选择第1个元素5会和2交换，那么原序列中2个5的相对前后顺序就被破坏了，所以选择排序不是一个稳定的排序算法
    public void selectSort() {
        for (int i = 0; i < a.length; i++) {
            int min = i;
            for (int j = i + 1; j < a.length; j++) {
                if (a[j] < a[min]) min = j;
            }
            swap(i, min);
        }
    }
    //    插入排序的思想是这样的，第一层for循环表示要循环n次，且每次循环要操作的主体是a[i]，第二层循环是对
    //    a[i]的具体操作，是从原数祖第i个位置起，向前比较，所以插入排序的平均时间复杂度也是O(n^2).
    //    比较是从有序序列的末尾开始，也就是想要插入的元素和已经有序的最大者开始比起，
    //    如果比它大则直接插入在其后面，否则一直往前找直到找到它该插入的位置。如果碰见一个和插入元素相等的，
    //    那么插入元素把想插入的元素放在相等元素的后面。所以，相等元素的前后顺序没有改变，
    //    从原无序序列出去的顺序就是排好序后的顺序，所以插入排序是稳定的。
    void insertSort() {
        for (int i = 1; i < a.length; i++) {
            int temp = a[i], j = i;
            while (j > 0 && a[j - 1] > temp) {
                a[j] = a[j - 1];
                j--;
            }
            a[j] = temp;
        }
    }
 

    //    1)        最好情况：序列是升序排列，在这种情况下，需要进行的比较操作需（n-1）次。后移赋值操作为0次。即O(n)
    //    2)        最坏情况：O(nlog2n)。
    //    3)        渐进时间复杂度（平均时间复杂度）：O(nlog2n)
    //    希尔排序是不稳定的。因为在进行分组时，相同元素可能分到不同组中，改变相同元素的相对顺序
    public void hillsort() {
        int h = 1;
        while (h < a.length / 3) {
            h = h * 3 + 1;
        }
        while (h > 0) {
            for (int i = 1; i < a.length; i++) {
                int temp = a[i], j = i;
                while (j > h - 1 && a[j - h] > temp) {
                    a[j] = a[j - h];
                    j -= h;
                }
                a[j] = temp;
            }
            h = (h - 1) / 3;
        }
    }

//    二分查找排序是稳定的，不会改变相同元素的相对顺序， 
    //    1. 时间复杂度：O(n^2)
    //    二分查找插入位置，因为不是查找相等值，而是基于比较查插入合适的位置，所以必须查到最后一个元素才知道插入位置。
    //    二分查找最坏时间复杂度：当2^X>=n时，查询结束，所以查询的次数就为x，而x等于log2n（以2为底，n的对数）。即O(log2n)
    //    所以，二分查找排序比较次数为：x=log2n
    //    二分查找插入排序耗时的操作有：比较 + 后移赋值。时间复杂度如下：
    //    1)        最好情况：查找的位置是有序区的最后一位后面一位，则无须进行后移赋值操作，其比较次数为：log2n  。即O(log2n)
    //    2)        最坏情况：查找的位置是有序区的第一个位置，则需要的比较次数为：log2n，需要的赋值操作次数为n(n-1)/2加上 (n-1) 次。即O(n^2)
    //    3)        渐进时间复杂度（平均时间复杂度）：O(n^2)
    void halfInsertSort() {
        for (int i = 1; i < a.length; i++) {
            if (a[i] > a[i - 1]) {
                continue;
            }
            int temp = a[i], left = 0, right = i - 1;
            while (left <= right) {
                int mid = (left + right) / 2;
                if (a[mid] > temp)
                    right = mid - 1;
                else
                    left = mid + 1;
            }
            for (int j = i; j > left; j--) {
                a[j] = a[j - 1];
            }
            a[left] = temp;
        }
    }
   

   public void mergeSort(int left, int right) {
        if (left >= right) return;
        int mid = (left + right) / 2;
        mergeSort(left, mid);
        mergeSort(mid + 1, right);
        merge(left, mid, mid + 1, right);
   }
   private void merge(int lb, int le, int rb, int re) {
        int[] temp = new int[a.length];
        int leftbegin = lb;
        int index = lb;
        while (lb <= le && rb <= re) {
            if (a[lb] < a[rb])
                temp[index++] = a[lb++];
            else
                temp[index++] = a[rb++];
        }
        while (lb <= le) {
            temp[index++] = a[lb++];
        }
        while (rb <= re) {
            temp[index++] = a[rb++];
        }
       
        while (leftbegin <= re) {
            a[leftbegin] = temp[leftbegin];
            leftbegin++;
        }
    }

1》归并排序的步骤如下：

       Divide: 把长度为n的输入序列分成两个长度为n/2的子序列。

       Conquer: 对这两个子序列分别采用归并排序。      

       Combine: 将两个排序好的子序列合并成一个最终的排序序列。

2》时间复杂度：

这是一个递推公式（Recurrence），我们需要消去等号右侧的T(n)，把T(n)写成n的函数。其实符合一定条件的Recurrence的展开有数学公式可以套，这里我们略去严格的数学证明，只是从直观上看一下这个递推公式的结果。当n=1时可以设T(1)=c1，当n>1时可以设T(n)=2T(n/2)+c2n，我们取c1和c2中较大的一个设为c，把原来的公式改为：

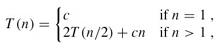这样计算出的结果应该是T(n)的上界。下面我们把T(n/2)展开成2T(n/4)+cn/2（下图中的(c)），然后再把T(n/4)进一步展开，直到最后全部变成T(1)=c（下图中的(d)）：

 

 

       把图(d)中所有的项加起来就是总的执行时间。这是一个树状结构，每一层的和都是cn，共有lgn+1层，因此总的执行时间是cnlgn+cn，相比nlgn来说，cn项可以忽略，因此T(n)的上界是Θ(nlgn)。

       如果先前取c1和c2中较小的一个设为c，计算出的结果应该是T(n)的下界，然而推导过程一样，结果也是Θ(nlgn)。既然T(n)的上下界都是Θ(nlgn)，显然T(n)就是Θ(nlgn)。

 

 

4）快速排序算法思想

基于分治的思想，是冒泡排序的改进型。首先在数组中选择一个基准点（该基准点的选取可能影响快速排序的效率，后面讲解选取的方法），然后分别从数组的两端扫描数组，设两个指示标志（lo指向起始位置，hi指向末尾)，首先从后半部分开始，如果发现有元素比该基准点的值小，就交换lo和hi位置的值，然后从前半部分开始扫秒，发现有元素大于基准点的值，就交换lo和hi位置的值，如此往复循环，直到lo>=hi,然后把基准点的值放到hi这个位置。一次排序就完成了。以后采用递归的方式分别对前半部分和后半部分排序，当前半部分和后半部分均有序时该数组就自然有序了。

 

 

 

//    平均时间复杂度O（nlogn），最坏时间复杂度O（n*n）,辅助空间O（logn）<每次都要分给一个额外空间，而总共有logn次>
//    每次分成两段，那么分的次数就是logn了，每一次处理需要n次计算，那么时间复杂度就是nlogn了！
//    根据平均情况来说是O(nlogn),因为在数据分布等概率的情况下对于单个数据来说在logn次移动后就会被放到正确的位置上了。
//    最坏是O(n^2).这种情况就是数组刚好的倒序，然后每次去中间元的时候都是取最大或者最小。
//    稳定性：不稳定。

 public static int partition(int []array,int lo,int hi){
        //左右中抽取3个点，按照213的顺序排序，以左节点2作为pivot
        int mid=lo+(hi-lo)/2;
        if(array[mid]>array[hi]){
            swap(array[mid],array[hi]);
        }
        if(array[lo]>array[hi]){
            swap(array[lo],array[hi]);
        }
        if(array[mid]>array[lo]){
            swap(array[mid],array[lo]);
        }
        int key=array[lo]; //此时左节点lo值为key。后续准备放置到lo和hi重合的位置

        while(lo<hi){
            //从右开始找到比key值小的数据，写入lo
            while(array[hi]>=key&&hi>lo){
                hi--;
            }
            array[lo]=array[hi];

            //从左开始找到比key值大的数据，写入hi
            while(array[lo]<=key&&hi>lo){
                lo++;
            }
            array[hi]=array[lo];
        }

//        lo和hi重合时候,将key放入。此时hi左面的数都小于key，右面数大于key
        array[hi]=key;
        return hi;
    }

    public static void swap(int a,int b){
        int temp=a;
        a=b;
        b=temp;
    }
    public static void sort(int[] array,int lo ,int hi){
        if(lo>=hi){
            return ;
        }
        int index=partition(array,lo,hi);
        sort(array,lo,index-1);
        sort(array,index+1,hi);
    }