省选算法学习-数据结构-splay
Posted Orion545
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了省选算法学习-数据结构-splay相关的知识,希望对你有一定的参考价值。
于是乎,在丧心病狂的noip2017结束之后,我们很快就要迎来更加丧心病狂的省选了-_-||
所以从写完上一篇博客开始到现在我一直深陷数据结构和网络流的漩涡不能自拔
今天终于想起来写博客(只是懒吧......)
言归正传。
省选级别的数据结构比NOIP要高到不知道哪里去了。
noip只考一点线段树啊st表啊并查集啊之类的简单数据结构,而且应用范围很窄
但是省选里面对数据结构,尤其是高级数据结构的要求就高了很多,更有一些题目看着就是数据结构题,也没有别的做法。
因此掌握高级数据结构就成了准备省选的一项大任务。
这一个月(2017.12-2018.1)来,我学习了平衡树、可持久化线段树、link-cut-tree和树套树四种数据结构。就在这里都记录下来。
第一篇是平衡树中的splay
在讲splay之前,需要先给出平衡树的定义。
平衡树是一棵二叉搜索树。它除了具有二叉搜索树的全部特征之外,还具有一个关键性的特征:“平衡”,即任意节点的左右子树高度差不超过1。
这个特性决定了它在面对特殊数据(例如那种专门卡普通二叉搜索树的数据)时,能够非常稳定的解决,只是牺牲了一些时间复杂度常数,但是基本不会被卡掉。
平衡树有非常多的实现方式,包括splay,treap,替罪羊树,红黑树,sbt(size balanced tree即严格平衡),AVL等
这篇文章则主要专注于splay
splay,意为“伸展”,故其中文名叫“伸展树”,核心是在二叉树上进行伸展操作,以此来保证树的平衡。
自然,伸展操作就成了splay树的核心,也是它和普通二叉树(二叉搜索树)的唯一的一点不同。
为方便描述,本文中统一称呼如下:
当前节点的编号为x,其父亲为fa[x],其左右儿子为ch[x][0]和ch[x][1],整棵树的根节点编号为root
splay操作的核心是旋转操作,又称rotate。它的特性是能够在不改变树的中序遍历(即满足原二叉搜索树性质)的条件下,改变树的形态,以此调整两棵子树之间的平衡。
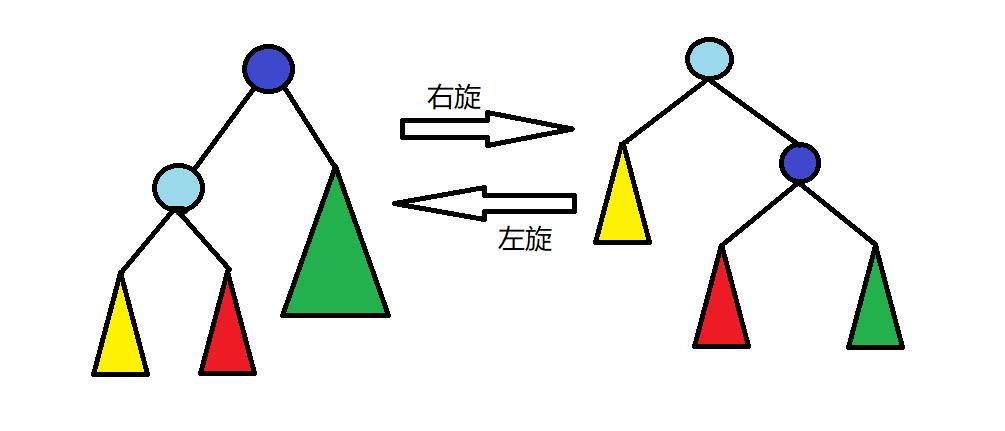
左右两图中三角形代表一整棵子树,圆则代表一个节点。
可以看到在两幅图中,整棵树的中序遍历都是“黄-浅蓝-红-深蓝-绿”,但是树的形态,以及根节点左右子树的深度却改变了。
因此可知,只要我们不断地进行左旋和右旋操作,一课不平衡的二叉树(例如一条链)一定可以被旋转成平衡的。
下面给出代码:
1 //get函数的作用是得到节点x是其父亲的左二子还是右儿子 2 int get(int x){ 3 return ch[fa[x]][1]==x; 4 } 5 //rotate函数将左旋和右旋集成。当x是左儿子的时候只能右旋,当x是右儿子的时候只能左旋 6 void rotate(int x){ 7 int f=fa[x],ff=fa[f],son=get(x); 8 //f是x的父节点,ff是f的父节点 9 push(f);push(x); 10 ch[f][son]=ch[x][son^1]; 11 if(ch[f][son]) fa[ch[f][son]]=f; 12 ch[x][son^1]=f; 13 fa[f]=x; 14 if(ff) ch[ff][ch[ff][1]==f]=x; 15 fa[x]=ff; 16 update(f);update(x); 17 }
rotate(x)函数的时间复杂度为O(1)
接下来的就是splay操作
splay操作的的过程用一句话来说,就是多次调用rotate函数,使节点x成为目标节点to的儿子
首先显然可以想到调用循环,每次循环中rotate(x),并检测fa[x]是不是to。
很遗憾的是,这样的splay会被一些特殊数据卡掉,不能严格保证平衡
这种单旋splay因此被戏称为spaly
实际应用中为了保证平衡性,splay树的splay操作运用了双旋的技巧。
双旋,即为每次循环中依据不同的情况,每个循环节中调用两次rotate函数,分为以下两种情况:
情况一:get(x) == get(fa[x]) (其中get函数意义见上一代码块)
此时应该先rotate(fa[x]),再rotate(x),如图所示:
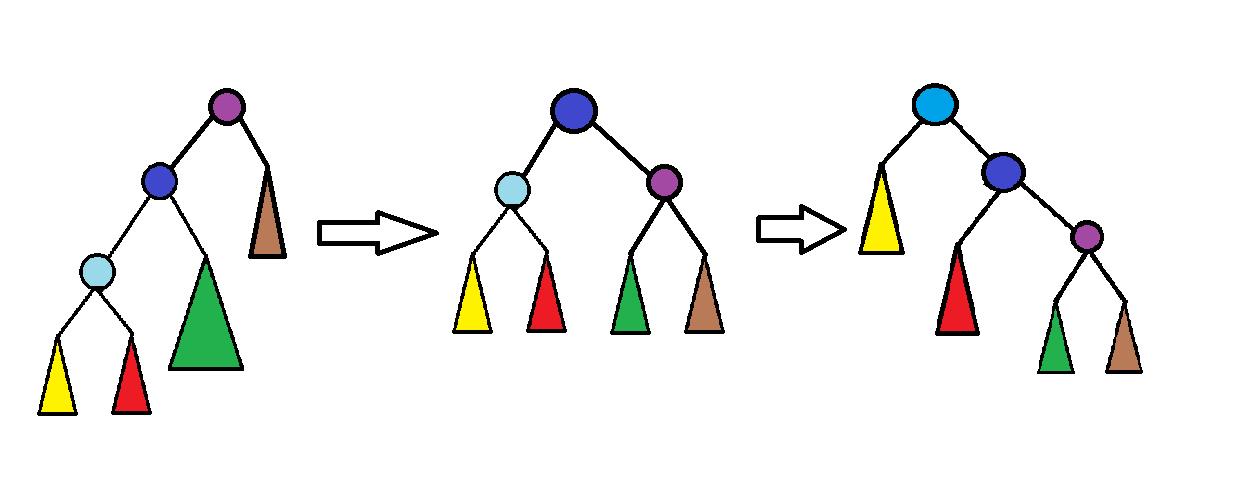
这样能够让原期望复杂度最大的,以浅蓝色节点为根的子树复杂度大大下降,平衡了三棵子树的复杂度
(其实这个具体原理非常复杂。若真正想搞清楚,可以去看tarjan教授的论文%%%)
情况二:get(x)!=get(fa[x])
这种情况下应该直接调用两次rotate(x),如下图:
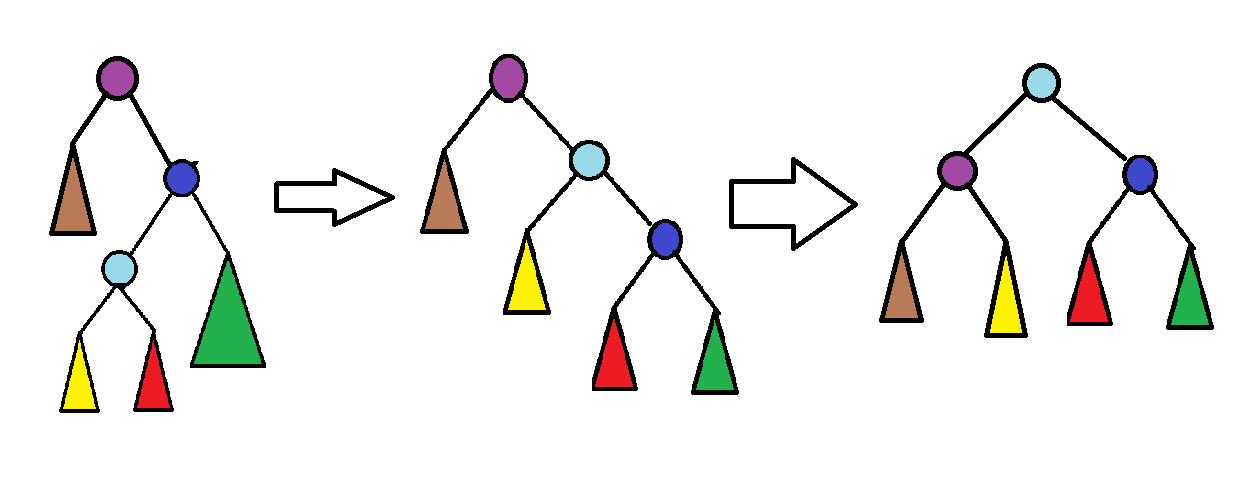
解释不多说,看图就清楚了,肯定平衡。
splay操作由于已经有rotate操作的集成函数,因此代码很短,如下:
1 //其实很多题目中并不涉及到splay(x,to),而是只涉及splay(x,fa[root]),即使x成为根节点。那样会简单很多。 2 void splay(int x,int to){ 3 push(x);//push操作是在更下传azy标记,详见后文 4 if(x==to||fa[x]==to) return; 5 for(int f;(f=fa[x])&&f!=to;rotate(x)){ 6 push(fa[fa[x]]);push(fa[x]);push(x); 7 if(fa[f]!=to) 8 rotate((get(x)==get(f))?f:x); 9 if(fa[x]==to) break; 10 } 11 update(x); 12 if(to==0) root=x; 13 }
splay(x,to)函数的时间复杂度为均摊下O(log n)
好了,到这里splay树的核心操作splay已经讲完了。
splay因为本质是一棵二叉搜索树,因此它也可以实现和二叉搜索树相同的操作,包括求rank,给定初始数列建树,插入节点,删除节点等。这个时候它是作为一棵二叉搜索树存在的。唯一的不同就是它会在每一次操作结束以后调用splay函数,从某一个节点开始伸展,用这样的方式保证树的平衡。例如在插入操作结束后,从新插入的节点x开始splay(x)到树根,或者是在求第k大的元素时,找到该元素后将它splay到根。
一道例题:tyvj 1728 普通平衡树
实际上是treap模板题,也可以用普通的bst做,但会被卡。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 inline int read(){ 7 int re=0,flag=1;char ch=getchar(); 8 while(ch>\'9\'||ch<\'0\'){ 9 if(ch==\'-\') flag=-1; 10 ch=getchar(); 11 } 12 while(ch>=\'0\'&&ch<=\'9\') re=(re<<1)+(re<<3)+ch-\'0\',ch=getchar(); 13 return re*flag; 14 } 15 int n,m,cnt,root; 16 int fa[300010],ch[300010][2],siz[300010],num[300010],w[300010]; 17 void clear(int x){fa[x]=ch[x][1]=ch[x][1]=siz[x]=num[x]=w[x]=0;} 18 void update(int x){siz[x]=siz[ch[x][0]]+siz[ch[x][1]]+num[x];} 19 int get(int x){return ch[fa[x]][1]==x;} 20 void rotate(int x){ 21 int f=fa[x],ff=fa[f],son=get(x); 22 ch[f][son]=ch[x][son^1]; 23 if(ch[f][son]) fa[ch[f][son]]=f; 24 fa[f]=x;ch[x][son^1]=f; 25 fa[x]=ff; 26 if(ff) ch[ff][ch[ff][1]==f]=x; 27 update(f);update(x); 28 } 29 void splay(int x){ 30 for(int f;f=fa[x];rotate(x)) 31 if(fa[f]) 32 rotate((get(f)==get(x))?f:x); 33 root=x; 34 } 35 void insert(int x,int pos){ 36 if(x==w[pos]){ 37 num[pos]++;splay(pos); 38 return; 39 } 40 if(x<w[pos]){ 41 if(!ch[pos][0]){ 42 clear(++cnt); 43 fa[cnt]=pos;w[cnt]=x;siz[cnt]=1;num[cnt]=1; 44 if(pos) ch[pos][0]=cnt; 45 splay(cnt); 46 } 47 else insert(x,ch[pos][0]); 48 } 49 else{ 50 if(!ch[pos][1]){ 51 clear(++cnt); 52 fa[cnt]=pos;w[cnt]=x;siz[cnt]=1;num[cnt]=1; 53 if(pos) ch[pos][1]=cnt; 54 splay(cnt); 55 } 56 else insert(x,ch[pos][1]); 57 } 58 } 59 int getrank(int x,int pos){ 60 if(w[pos]==x){ 61 splay(pos); 62 return siz[ch[pos][0]]+1; 63 } 64 if(w[pos]>x) return getrank(x,ch[pos][0]); 65 else return getrank(x,ch[pos][1]); 66 } 67 int getrankval(int x,int pos){ 68 if(x>siz[ch[pos][0]]&&x<=siz[ch[pos][0]]+num[pos]){ 69 splay(pos); 70 return w[pos]; 71 } 72 if(x<=siz[ch[pos][0]]) return getrankval(x,ch[pos][0]); 73 else return getrankval(x-siz[ch[pos][0]]-num[pos],ch[pos][1]); 74 } 75 //pre和suf函数是在splay结束后,从根节点(待求节点)开始,向左(向右)走一步,然后反过来一直走,走到没有右(左)儿子为止,把该节点的值返回。由二叉搜索树性质可得,这个点是比输入节点小的所有节点中最大的那个。 76 int pre(){ 77 int pos=ch[root][0]; 78 while(ch[pos][1]) pos=ch[pos][1]; 79 return pos; 80 } 81 int suf(){ 82 int pos=ch[root][1]; 83 while(ch[pos][0]) pos=ch[pos][0]; 84 return pos; 85 } 86 //del函数同样是在splay完以后,直接删除根节点(splay上去的所要求的节点)。方法是把左子树的最大值(即pre())splay到根,此时左子树树根没有右儿子,再把源根的右子树接上去即可。 87 void del(int x){ 88 int rk=getrank(x,root); 89 if(num[root]>1){ 90 num[root]--;return; 91 } 92 if(!ch[root][0]&&!ch[root][1]){ 93 clear(root);return; 94 } 95 if(!ch[root][0]){ 96 root=ch[root][1]; 97 clear(fa[root]);fa[root]=0; 98 return; 99 } 100 if(!ch[root][1]){ 101 root=ch[root][0]; 102 clear(fa[root]);fa[root]=0; 103 return; 104 } 105 int rt=root,left=pre();splay(left); 106 ch[root][1]=ch[rt][1]; 107 fa[ch[rt][1]]=root; 108 clear(rt);update(root); 109 } 110 int main(){ 111 int i,t1,t2; 112 n=read(); 113 for(i=1;i<=n;i++){ 114 t1=read();t2=read(); 115 if(t1==1) insert(t2,root); 116 if(t1==2) del(t2); 117 if(t1==3) insert(t2,root),printf("%d\\n",getrank(t2,root)),del(t2); 118 if(t1==4) printf("%d\\n",getrankval(t2,root)); 119 if(t1==5) insert(t2,root),printf("%d\\n",w[pre()]),del(t2); 120 if(t1==6) insert(t2,root),printf("%d\\n",w[suf()]),del(t2); 121 } 122 }
需要说明的是,splay树的每一个操作时间效率都是O(log n),但是它的常数在平衡树中是比较大的。因此若是有treap或者其他平衡树能实现的题目,用其他的平衡树可以避免卡常。
那么既然如此,splay又有什么特别的作用呢?
这就是接下来要讲的,splay的另一种用处。
先以一个小目标(雾)引入:
给出一个区间,长度为n,以及m次区间翻转操作(即把整个区间镜像过来),n,m <= 100,000
输出最后的序列。
如果不讨论某蜜汁无敌整体二分之类的方法,直接正面硬肛♂的话,好像有点难做。
不管是什么奇奇怪怪的结构都没法满足提取区间然后反过来这么一个蜜汁要求。
那么现在就是splay发挥大用处的时候了。
我们把这个序列建成一棵splay树,其中每一个节点的rank就是它在原序列中的位置。
例如某个splay树节点,它的中序遍历是全树的第x位,那么它也就是原数列的第x个数。
换句话说,这颗新建的splay树的中序遍历就是原数列。
理解了这一部分之后再往下看,我们现在引入splay区间提取的核心操作:
设将要提取的区间为 [l,r] ,则进行如下操作:
splay排名为 l-1 的点到根,再把排名为 r+1 的节点splay到 排名为 l-1 的节点下面。那么排名为 r+1 的节点的左子树就是节点区间 [l,r]。
如图:
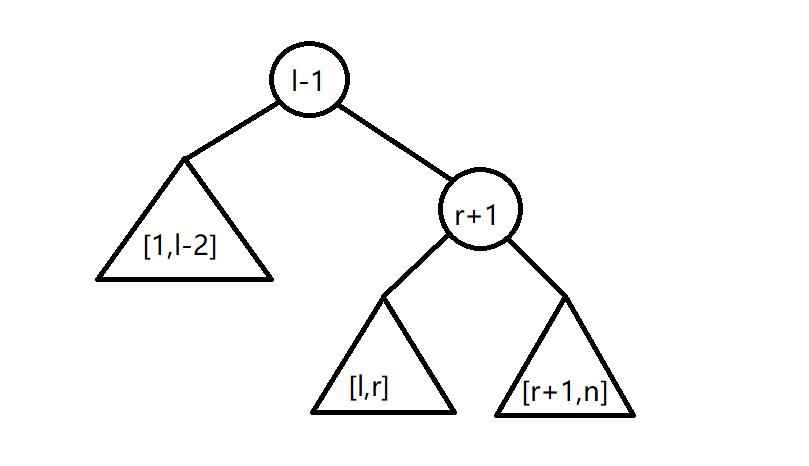
因为这颗splay满足二叉搜索树性质,因此区间[l,r]的提取的正确性显然。
然后我们就可以在这颗子树上为所欲为了(≖ᴗ≖)✧
在这颗子树的根节点上加一个lazy标记,然后在每次修改树的形态之前push一下,就可以很好的维护了。
同理,splay也可以通过这种方式完成区间加、区间求和、区间求最小值之类的操作。
不过这种splay无法完成求第k大,因为求第k大的操作依赖于键值的有序性,但是这颗splay树并不满足,所以无法达成。
一道例题:poj 3580 SuperMemo
原题链接:http://poj.org/problem?id=3580
大意就是让你完成以下操作:单点插入,单点删除,区间加,区间翻转,区间旋转(见原题),求区间最小值。
可以用splay很好的维护,甚至可以说是一道很全的模板题了。
rev操作只要把前一半区间“剪”下来,再“粘”到后一半区间的后面即可。
代码:
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #define inf 0x7fffffff 6 using namespace std; 7 int n,m,root,cnt,tmp[300010]; 8 int fa[300010],ch[300010][2],w[300010],siz[300010]; 9 int minn[300010],lazy1[300010],lazy2[300010]; 10 void _swap(int &l,int &r){l^=r;r^=l;l^=r;} 11 int _min(int l,int r){return (l>r)?r:l;} 12 void clear(int x){ 13 fa[x]=ch[x][0]=ch[x][1]=w[x]=siz[x]=lazy1[x]=lazy2[x]=0; 14 } 15 void add(int x,int f){ 16 cnt++; 17 fa[cnt]=f;ch[cnt][0]=ch[cnt][1]=0;w[cnt]=minn[cnt]=x;siz[cnt]=1;lazy1[cnt]=lazy2[cnt]=0; 18 } 19 int get(int x){ 20 return ch[fa[x]][1]==x; 21 } 22 void update_add(int x,int k){ 23 if(x) lazy2[x]+=k,minn[x]+=k,w[x]+=k; 24 } 25 void update_rev(int x){ 26 if(!x) return; 27 _swap(ch[x][0],ch[x][1]); 28 lazy1[x]^=1; 29 } 30 void update(int x){ 31 if(!x) return; 32 siz[x]=1;minn[x]=w[x]; 33 if(ch[x][0]) siz[x]+=siz[ch[x][0]],minn[x]=_min(minn[x],minn[ch[x][0]]); 34 if(ch[x][1]) siz[x]+=siz[ch[x][1]],minn[x]=_min(minn[x],minn[ch[x][1]]); 35 } 36 void push(int x){ 37 if(!x) return; 38 if(lazy1[x]){ 39 update_rev(ch[x][0]); 40 update_rev(ch[x][1]); 41 lazy1[x]=0; 42 } 43 if(lazy2[x]){ 44 update_add(ch[x][0],lazy2[x]); 45 update_add(ch[x][1],lazy2[x]); 46 lazy2[x]=0; 47 } 48 } 49 void rotate(int x){ 50 int f=fa[x],ff=fa[f],son=get(x); 51 push(f);push(x); 52 ch[f][son]=ch[x][son^1]; 53 if(ch[f][son]) fa[ch[f][son]]=f; 54 ch[x][son^1]=f; 55 fa[f]=x; 56 if(ff) ch[ff][ch[ff][1]==f]=x; 57 fa[x]=ff; 58 update(f);update(x); 59 } 60 void splay(int x,int to){ 61 push(x); 62 if(x==to||fa[x]==to) return; 63 for(int f;(f=fa[x])&&f!=to;rotate(x)){ 64 push(fa[fa[x]]);push(fa[x]);push(x); 65 if(fa[f]!=to) 66 rotate((get(x)==get(f))?f:x); 67 if(fa[x]==to) break; 68 } 69 update(x); 70 if(to==0) root=x; 71 } 72 int build(int l,int r,int f){ 73 int mid=(l+r)>>1,tt; 74 add(tmp[mid],f);tt=cnt; 75 if(mid>l) ch[tt][0]=build(l,mid-1,tt); 76 if(mid<r) ch[tt][1]=build(mid+1,r,tt); 77 update(tt); 78 return tt; 79 } 80 int rank(int k,int pos){ 81 push(pos); 82 if(siz[ch[pos][0]]+1==k) return pos; 83 if(siz[ch[pos][0]]>=k) return rank(k,ch[pos][0]); 84 else return rank(k-siz[ch[pos][0]]-1,ch[pos][1]); 85 } 86 void add(int l,int r,int k){ 87 int x=rank(l,root),y=rank(r+2,root); 88 splay(x,0);splay(y,x); 89 update_add(ch[y][0],k); 90 } 91 void rev(int l,int r){ 92 int x=rank(l,root),y=rank(r+2,root); 93 splay(x,0);splay(y,x); 94 lazy1[ch[y][0]]^=1; 95 _swap(ch[ch[y][0]][0],ch[ch[y][0]][1]); 96 } 97 void res(int l1,int r1,int l2,int r2){ 98 int x=rank(l2,root),y=rank(r2+2,root); 99 splay(x,0);splay(y,x); 100 int tt=ch[y][0]; 101 ch[y][0]=0;fa[tt]=0; 102 x=rank(l1,root);y=rank(l1+1,root); 103 splay(x,0);splay(y,x); 104 ch[y][0]=tt;fa[tt]=y; 105 } 106 void ins(int p,int k){ 107 int x=rank(p+1,root),y=rank(p+2,root); 108 splay(x,0);splay(y,x); 109 add(k,y);ch[y][0]=cnt; 110 push(y);update(y); 111 push(x);update(x); 112 splay(y,0); 113 } 114 void del(int p){ 115 int x=rank(p,root),y=rank(p+2,root); 116 splay(x,0);splay(y,x); 117 clear(ch[y][0]);ch[y][0]=0; 118 update(y);update(x); 119 } 120 int getmin(int l,int r){ 121 int x=rank(l,root),y=rank(r+2,root); 122 splay(x,0);splay(y,x); 123 return minn[ch[y][0]]; 124 } 125 int main(){ 126 int i,t1,t2,t3;char s[10]; 127 scanf("%d",&n); 128 for(i=1;i<=n;i++) scanf("%d",&tmp[i]); 129 tmp[0]=tmp[n+1]=inf; 130 root=build(0,n+1,0); 131 scanf("%d",&m); 132 for(i=1;i<=m;i++){ 133 scanf("%s",s); 134 if(s[0]==\'A\'){ 135 scanf([转]省选算法汇总
