容斥原理

Posted 2020-10-19 lokiii

简单的容斥原理可以通过画文氏图来理解：
\\( \\left | S_1\\cup S_2 \\right |=\\left | S_1 \\right |+\\left | S_2 \\right |-\\left | S_1\\cap S_2 \\right | \\)

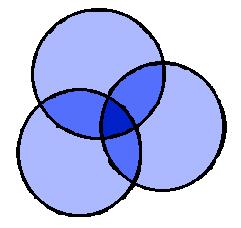
\\( \\left | S_1\\cup S_2 \\cup S_3 \\right |=\\left | S_1 \\right |+\\left | S_2 \\right |+\\left | S_3 \\right |-\\left | S_1\\cap S_2 \\right |-\\left | S_1\\cap S_3 \\right |-\\left | S_2\\cap S_3 \\right |-\\left | S_1\\cap S_2 \\cap S_3 \\right | \\)

可得：

\\[\\left |S_1 \\cup S_2 \\cup ...S_n \\right |=\\sum_{i=1}^{n}((-1)^{n-1}*\\sum_{j=1}^{C_{n}^{i}}\\left |S_{x1} \\cap S_{x2} \\cap...S_{xi} \\right|) \\]

后面那个\\( \\sum \\)里是\\( i \\) 个元素的一种组合

经典问题：

一、不定方程

首先考虑不定方程\\( x_1+x_2+...+x_n=m \\)的非负整数解个数
是\\( C_{x+m-1}^{m-1} \\)
用隔板法比喻来解释一下：考虑现在有\\( n-1 \\)个隔板，要插进\\( m \\)个球中间，隔板允许放进同一位置。首先不能放进同一位置的很简单，组合数即可，而对于允许放进同一位置的情况，考虑把放在同一位置的也用球隔开，那么相当于多加了\\( m \\)个球的不允许放进同一位置。

那么现在考虑增加一些限制：\\( x_i \\)的最大值为\\( b[i] \\)。这个时候就要考虑用容斥原理了。
对于\\( b[i] \\)均相同时，设\\( x=b[i] \\)：
枚举有至少\\( k \\)个不满足的条件，那么这\\( k \\)个不满足的条件得组合个数为\\( C_{m-1}^{k} \\)，这\\( k \\)个不满足的条件每个至少是\\( x+1 \\)，在总数中去掉不满足条件的\\( k \\)个\\( x+1 \\)，然后在剩下的数中使用隔板法，方案数为\\( C_{n-(k+1)*x+m-2}^{m-2} \\)
例题：
hdu 5201 http://www.cnblogs.com/lokiii/p/8214425.html

对于不等于的情况，\\( 2^n \\)枚举每种不满足的条件组合方案即可。
例题：
Codeforces 451E http://www.cnblogs.com/lokiii/p/8203480.html

二、错排问题

错排的性质就是第\\( i \\)个位置上的数字不等于\\( i \\)。也就是\\( d[i]!=i \\)
那么设\\( D_n \\)为\\( n \\)个数字的错排方案数，和上面差不多的，加上至少0个\\( d[i]=i \\)减去至少1个\\( d[i]=i \\)加上至少2个\\( d[i]=i \\)......

\\[D_n=n!-\\sum_{t=1}^{n}(-1)^{t-1}\\sum_{i_1<i_2<...<i_t}(n-t)! \\]

\\[D_n=n!+\\sum_{t=1}^{n}(-1)^tC_{n}^{t}(n-t)! \\]

\\[D_n=n!+\\sum_{t=1}^{n}(-1)^t\\frac{n!}{t!} \\]

\\[D_n=n!\\sum_{t=0}^{n}\\frac{(-1)^t}{t!} \\]

例题：
bzoj 4517 http://www.cnblogs.com/lokiii/p/8215044.html