2.机器学习技法- Dual Support Vector Machine

Posted 2020-10-19 tmortred

Lecture 2.  Dual Support Vector Machine

2.1 Motivation of Dual Suppor Vector Machine

将 linear support vector machine 加上 feature transformation 就能得到 nonlinear support vector machine。这样做的好处，我们可以利用 svm 和 feature transformation 的优良特性_Q1：较小的 VC Dimension （SVM）、复杂的边界（feature transformation）。但是这样又引入了新的问题，计算量太大如图 2-1 所示

                                                              图  2-1

QP 有 $\\tilde{d}$ + 1 个变量和 N 个约束， 如果变量数太多计算量太大。现在问题就变成如何在 $\\tilde{d}$ 很大的时候，如何求解动态规划 QP？

                                                      图  2-2 

如图 2-2 所示，如果我们能将原始问题（左边）转换成另外一个对等问题（右边）。我们就不用考虑 $\\tilde{d}$ 的影响了。图 2-2 右图相关公式的证明过程很复杂， 林老师采用启发的方式带我们过一遍的证明的思路。首先是如图 2-3 所示，左半图是方程的约束， 它和我们之前推导增广误差时很像单不同。增广误差的 $\\lambda$ 是指定的， SVM 中的 $\\lambda $ 是一个计算出的值（其实有 N个 约束，就有 N 个 $\\lambda$）。

                                                                  图 2-3 

 

使用 lagrange 乘子法，结果如图 2-4 所示

                         图 2-4 lagrange 乘子法将有约束方程转化为无约束方程

 现在问题就变成求解公式  $\\frac{1}{2}w^Tw + \\sum\\alpha_{n}(1- y_{n}(w^Tz_{n}+b))$ ， 经过一步步证明将公式变成图 2-4 所示公式（为什么$\\alpha_{n}$ 要大于 0？ 没有任何证明，只能将 $\\alpha$ 类比 增广误差中的 $\\lambda$， 因为 $\\lambda$ 大于等于 0 所以 $\\alpha $ 也大于等于 0。真的是启发式证明。 后续的课程中可以看出 $\\alpha$ 的取值范围有一定的意义,但是我忘了这意义是个啥。对于 soft SVM 有 0 ≤ $\\alpha$ ≤ C）

                  图 2-5

2.2 Lagrange Dual SVM

图 2-5 所示的公式不是很容易求解，但是它可以化简为一个简单版本，如图 2-6 所示（启发式证明）。

                                                                       图  2-6 

 似乎图 2-6 也没有做什么简化，和图 2-5 公式一比照无非就是将 min 和 max 的位置换掉。但是图 2-6 中公式，我们先要做 min 后做 max， 我们比较喜欢做 min。因为对于可导的公式，可以使用求导公式。这样经过化简我们得到一个 KKT 问题（KKT 问题，看了就忘。没办法建立直观的感性认识），如图 2-7 所示

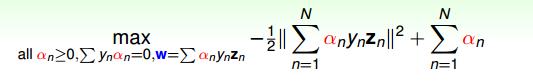
                                       图 2-7 

 

2.3 Solving Dual SVM

 将图 2 -7 的问题（其实要乘 -1 ）展开后如图 2-8 所示，

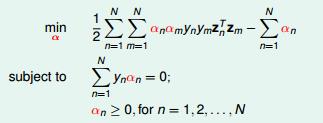
                            图 2-8

 现在我们来回忆一下，求解 optimal（b，w） 所需的条件，如图 2-9 所示。我们只要求出 $\\alpha_{optimal}$ 就能求出 $w_{optimal}$。用任何一个非 0 的 $\\alpha$ 就能求出 b （$\\alpha_{n} (1 - y_{n}(w^tz_{n})) =0 \\Longrightarrow b = y_{n} - w^tz_{n} $）。

因为 $\\alpha_{n} (1 - y_{n}(w^tz_{n}+b)) = 0$ 代表 $a_{n}$ 和 $1 - y_{n}(w^tz_{n} +b)$ 不能同时非 0，这样我们就得到 support vector ，如图 2-10 所示

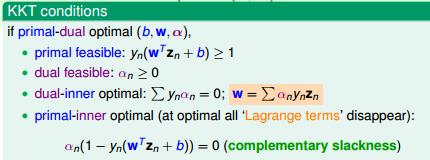
                                  图 2-9

             图 2-10 

2.4 Messages behind Dual SVM

        support vector machine 中的 support vector 是什么？ support vector 肯定是在 fat boundary 中（hard SVM 要求将数据全部分掉），这样那些不在 boundary 中样本数据不需要计算。另外就算在 fat boundary 边界上的点也不一定是 support vector ，如图 2-10所示。support vector 是怎么算出来的呢？ 采用 dual optimal solution 求出的。

现在我们来看一个有趣的现象， $w_{SVM} = \\sum\\alpha_{n}(y_{n}z_{n})$ 和  PLA 中的 w 很像。always we call w ‘represented’ by data ， 对 SVM 而言有 w ‘represented’ by SVs only 

                        图 2-11 多种算法的 w_Q3

最后我们来对比一下 primal Hard-Margin SVM 和 Dual Hard-Margin SVM， 如图 2-12 所示

 

                 图 2-12  A tale of two SVMs

到目前为止，似乎一切都很完美。我们采用对偶方法，不用考虑 $\\tilde{d}$ 了？似乎这样的，但是我们是把 $\\tilde{d}$ 的计算放到对偶问题的转化矩阵了， 如图 2-13 所示

                     图 2-13 

最终用一张图片结束本节笔记

                       图  2-14

 

 

题外话： 

Q1： 林老师的切入 SVM 相关话题的角度和其它书籍写的不一样

T1： 为什么就算我从头手敲公式一次，还是对课程内容没什么影响？之前的 VC Dimension 课程，我可是写一篇笔记就能感觉自己在进步。记不住复杂公式，烦躁！

Q2： 图 2-8 所示的公式，还是不会解啊！如图 2-Q-1 所示，不知道为什么要输入 $ a ≥ 0, 0 ≤ a$

                       图  2-Q-1

Q3：林老师在《基石》中前几节就讨论了 PLA 不是没有原因的。在《基石》和《技法》PLA 都友情客串好多次不同算法间对照分析。林老师 v587！后续的章节中还有一个很重要的结论对于 L2 regularized linear model 都能用 kernel tricks ！， L2 regularized 这个词已经不在作为一个  regularized method 给各个算法打工，都有自己的定律了。 L2 regularied v587！