前面的话
本文将详细介绍算法模式,包括递归、动态规划和贪心算法
递归
递归是一种解决问题的方法,它解决问题的各个小部分,直到解决最初的大问题。通常涉及函数调用自身
能够像下面这样直接调用自身的方法或函数,是递归函数:
var recursiveFunction = function(someParam){ recursiveFunction(someParam); };
能够像下面这样间接调用自身的函数,也是递归函数:
var recursiveFunction1 = function(someParam){ recursiveFunction2(someParam); }; var recursiveFunction2 = function(someParam){ recursiveFunction1(someParam); };
假设现在必须要执行recursiveFunction,结果是什么?单单就上述情况而言,它会一直执行下去。因此,每个递归函数都必须要有边界条件,即一个不再递归调用的条件(停止点), 以防止无限递归
【javascript调用栈大小的限制】
如果忘记加上用以停止函数递归调用的边界条件,会发生什么呢?递归并不会无限地执行下去;浏览器会抛出错误,也就是所谓的栈溢出错误(stack overflow error)
每个浏览器都有自己的上限,可用以下代码测试:
var i = 0; function recursiveFn () { i++; recursiveFn(); } try { recursiveFn(); } catch (ex) { alert(‘i = ‘ + i + ‘ error: ‘ + ex); }
在Chrome中,这个函数执行了15699次,而后浏览器抛出错误RangeError: Maximum call stack size exceeded(超限错误:超过最大调用栈大小)
ECMAScript 6有尾调用优化(tail call optimization)。如果函数内最后一个操作是调用函数,会通过“跳转指令”(jump) 而不是“子程序调用”(subroutine call)来控制。也就是说,在ECMAScript 6中,这里的代码可以一直执行下去。所以,具有停止递归的边界条件非常重要
【斐波那契数列】
斐波那契数列的定义如下:
1、1和2的斐波那契数是 1;
2、n(n>2)的斐波那契数是(n-1)的斐波那契数加上(n-2)的斐波那契数
下面来实现斐波那契函数
function fibonacci(num){ if (num === 1 || num === 2){ return 1; } return fibonacci(num - 1) + fibonacci(num - 2); }
我们已经知道,当n大于2时,Fibonacci(n)等于Fibonacci(n-1)+Fibonacci(n-2)。现在,斐波那契函数实现完毕。试着找出6的斐波那契数,其会产生如下函数调用:
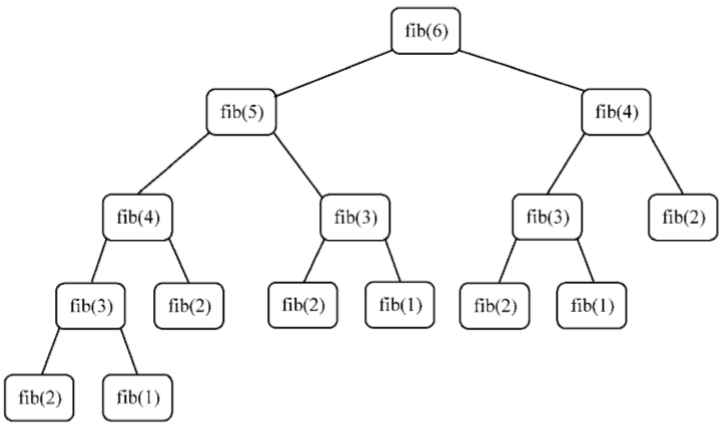
也可以用非递归的方式实现斐波那契函数:
function fib(num){ var n1 = 1, n2 = 1, n = 1; for (var i = 3; i<=num; i++){ n = n1 + n2; n1 = n2; n2 = n; } return n; }
为何用递归呢?更快吗?递归并不比普通版本更快,反倒更慢。但要知道,递归更容易理解,并且它所需的代码量更少。所以,用递归通常是因为它更容易解决问题
动态规划
动态规划(Dynamic Programming,DP)是一种将复杂问题分解成更小的子问题来解决的优化技术
动态规划和分而治之(归并排序和快速排序算法中用到的那种)是不同的方法。分而治之方法是把问题分解成相互独立的子问题,然后组合它们的答案,而动态规划则是将问题分解成相互依赖的子问题
用动态规划解决问题时,要遵循三个重要步骤:
1、定义子问题
2、实现要反复执行而解决子问题的部分
3、识别并求解出边界条件。
能用动态规划解决的一些著名的问题如下
1、背包问题:给出一组项目,各自有值和容量,目标是找出总值最大的项目的集合。这个问题的限制是,总容量必须小于等于“背包”的容量
2、最长公共子序列:找出一组序列的最长公共子序列(可由另一序列删除元素但不改变余下元素的顺序而得到)
3、矩阵链相乘:给出一系列矩阵,目标是找到这些矩阵相乘的最高效办法(计算次数尽可能少)。相乘操作不会进行,解决方案是找到这些矩阵各自相乘的顺序
4、硬币找零:给出面额为d1…dn的一定数量的硬币和要找零的钱数,找出有多少种找零的方法
5、图的全源最短路径:对所有顶点对(u, v),找出从顶点u到顶点v的最短路径
【最少硬币找零问题】
最少硬币找零问题是硬币找零问题的一个变种。硬币找零问题是给出要找零的钱数,以及可用的硬币面额d1…dn及其数量,找出有多少种找零方法。最少硬币找零问题是给出要找零的钱数,以及可用的硬币面额d1…dn及其数量,找到所需的最少的硬币个数
例如,有以下面额(硬币):d1=1,d2=5,d3=10,d4=25。如果要找36美分的零钱,可以用1个25美分、1个10美分和1个便士(1美分)。如何将这个解答转化成算法?最少硬币找零的解决方案是找到n所需的最小硬币数。但要做到这一点,首先得找到对每个x<n的解。然后,我们将解建立在更小的值的解的基础上
来看看算法:
function MinCoinChange(coins){ var cache = {}; this.makeChange = function(amount) { var me = this; if (!amount) { return []; } if (cache[amount]) { return cache[amount]; } var min = [], newMin, newAmount; for (var i=0; i<coins.length; i++){ var coin = coins[i]; newAmount = amount - coin; if (newAmount >= 0){ newMin = me.makeChange(newAmount); } if ( newAmount >= 0 && (newMin.length < min.length-1 || !min.length) && (newMin.length || !newAmount) ){ min = [coin].concat(newMin); console.log(‘new Min ‘ + min + ‘ for ‘ + amount); } } return (cache[amount] = min); }; }
为了更有条理,创建了一个类,解决给定面额的最少硬币找零问题
MinCoinChange类接收coins参数(行{1}),代表问题中的面额。对美国的硬币系统而言,它是[1, 5, 10, 25]。我们可以随心所欲传递任何面额。此外,为了更加高效且不重复计算值,我们使用了cache(行{2})。
接下来是makeChange方法,它也是一个递归函数,找零问题由它解决。首先,若amount不为正(< 0),就返回空数组(行{3});方法执行结束后,会返回一个数组,包含用来找零的各个面额的硬币数量(最少硬币数)。接着,检查cache缓存。若结果已缓存(行{4}),则直接返回结果;否则,执行算法。
我们基于coins参数(面额)解决问题。因此,对每个面额(行{5}),我们都计算newAmount(行{6})的值,它的值会一直减小,直到能找零的最小钱数(别忘了本算法对所有的x < amount都会计算makeChange结果)。若newAmount是合理的值(正值),我们也会计算它的找零结果(行{7})
最后,我们判断newAmount是否有效,minValue (最少硬币数)是否是最优解,与此同时minValue和newAmount是否是合理的值({行10})。若以上判断都成立,意味着有一个比之前更优的答案(行{11},以5美分为例,可以给5便士或者1个5美分镍币,1个5美分镍币是最优解)。 最后,返回最终结果(行{12})
测试一下这个算法:
var minCoinChange = new MinCoinChange([1, 5, 10, 25]); console.log(minCoinChange.makeChange(36));
要知道,如果我们检查cache变量,会发现它存储了从1到36美分的所有结果。以上代码的结果是[1, 10, 25]
【背包问题】
背包问题是一个组合优化问题。它可以描述如下:给定一个固定大小、能够携重W的背包,以及一组有价值和重量的物品,找出一个最佳解决方案,使得装入背包的物品总重量不超过W,且总价值最大
下面是一个例子:
物品 重量 价值 1 2 3 2 3 4 3 4 5
考虑背包能够携带的重量只有5。对于这个例子,我们可以说最佳解决方案是往背包里装入物品1和物品2,这样,总重量为5,总价值为7。
来看看背包算法:
function knapSack(capacity, weights, values, n) { var i, w, a, b, kS = []; for (i = 0; i <= n; i++) { kS[i] = []; } for (i = 0; i <= n; i++){ for (w = 0; w <= capacity; w++){ if (i == 0 || w == 0){ kS[i][w] = 0; } else if (weights[i-1] <= w){ a = values[i-1] + kS[i-1][w-weights[i-1]]; b = kS[i-1][w]; kS[i][w] = (a > b) ? a : b; //max(a,b) console.log(a + ‘ can be part of the solution‘); } else{ kS[i][w] = kS[i-1][w]; } } console.log(kS[i].join()); } return kS[n][capacity]; }
来看看这个算法是如何工作的。
行{1}:首先,初始化将用于寻找解决方案的矩阵ks[n+1][capacity+1]
行{2}:忽略矩阵的第一列和第一行,只处理索引不为0的列和行。
行{3}:物品i的重量必须小于约束(capacity)才有可能成为解决方案的一部分;否则,总重量就会超出背包能够携带的重量,这是不可能发生的。发生这种情况时,只要忽略它,用之前的值就可以了(行{5})。
行{4}:当找到可以构成解决方案的物品时,选择价值大的那个。
行{6}:最后,问题的解决方案就在这个二维表格右下角的后一个格子里
可以用开头的例子来测试这个算法:
var values = [3, 4, 5], weights = [2, 3, 4], capacity = 5, n = values.length; console.log(knapSack(capacity, weights, values, n)); //输出 7
下图举例说明了例子中kS矩阵的构造:
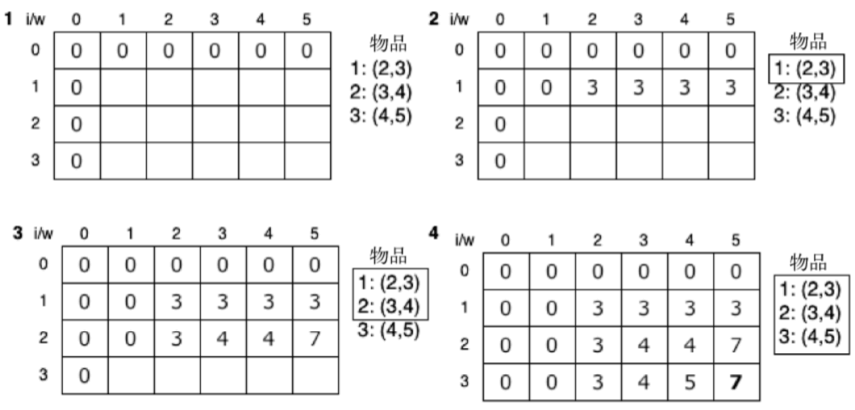
这个算法只输出背包携带物品价值的大值,而不列出实际的物品。我们可以增加下面的附加函数来找出构成解决方案的物品:
function findValues(n, capacity, kS, weights, values){ var i=n, k=capacity; console.log(‘Items that are part of the solution:‘); while (i>0 && k>0){ if (kS[i][k] !== kS[i-1][k]){ console.log(‘item ‘+i+‘ can be part of solution w,v: ‘ + weights[i-1] + ‘,‘ + values[i-1]); i--; k = k - kS[i][k]; } else { i--; } } }
可以在knapsack函数的行{6}之前调用这个函数。执行完整的算法,会得到如下输出:
解决方案包含以下物品: 物品2,重量:4,价值:3 物品1,重量:3,价值:2 总价值:7
【最长公共子序列(LCS)】
另一个经常被当作编程挑战问题的动态规划问题是最长公共子序列(LCS):找出两个字符串序列的长子序列的长度。长子序列是指,在两个字符串序列中以相同顺序出现,但不要求连续(非字符串子串)的字符串序列。
考虑如下例子:
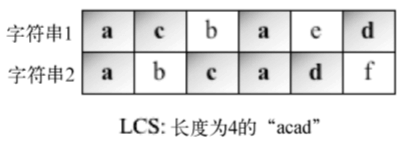
再看看下面这个算法:
function lcs2(wordX, wordY) { var m = wordX.length, n = wordY.length, l = [], solution = [], i, j, a, b; for (i = 0; i <= m; ++i) { l[i] = []; solution[i] = []; for (j = 0; j <= n; ++j) { l[i][j] = 0; solution[i][j] = ‘0‘; } } for (i=0; i<=m; i++) { for (j=0; j<=n; j++) { if (i == 0 || j == 0){ l[i][j] = 0; } else if (wordX[i-1] == wordY[j-1]) { l[i][j] = l[i-1][j-1] + 1; solution[i][j] = ‘diagonal‘; } else { a = l[i-1][j]; b = l[i][j-1]; l[i][j] = (a > b) ? a : b; //max(a,b) solution[i][j] = (l[i][j] == l[i - 1][j]) ? ‘top‘ : ‘left‘; } } console.log(l[i].join()); console.log(solution[i].join()); } printSolution(solution, l, wordX, wordY, m, n); return l[m][n]; } function printSolution(solution, l, wordX, wordY, m, n){ var a = m, b = n, i, j, x = solution[a][b], answer = ‘‘; while (x !== ‘0‘) { if (solution[a][b] === ‘diagonal‘) { answer = wordX[a - 1] + answer; a--; b--; } else if (solution[a][b] === ‘left‘) { b--; } else if (solution[a][b] === ‘top‘) { a--; } x = solution[a][b]; } console.log(‘lcs: ‘+ answer); }
如果用‘acbaed‘和‘abcadf‘两个字符串执行上面的算法,我们将得到输出4。用于构建结果的矩阵l看起来像下面这样。我们也可以用附加的算法来跟踪LCS的值
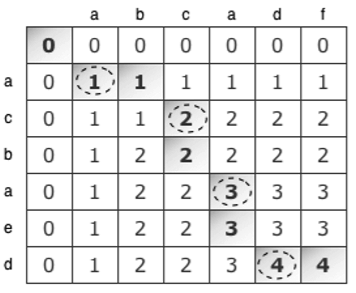
通过上面的矩阵,我们知道LCS算法的结果是长度为4的acad
【矩阵链相乘】
矩阵链相乘是另一个可以用动态规划解决的著名问题。这个问题是要找出一组矩阵相乘的最佳方式(顺序)
n行m列的矩阵A和m行p列的矩阵B相乘,结果是n行p列的矩阵C
考虑我们想做A*B*C*D的乘法。因为乘法满足结合律,所以我们可以让这些矩阵以任意顺序相乘。因此,考虑如下情况:
A是一个10行100列的矩阵
B是一个100行5列的矩阵
C是一个5行50列的矩阵
D是一个50行1列的矩阵
A*B*C*D的结果是一个10行1列的矩阵
在这个例子里,相乘的方式有五种
1、(A(B(CD))):乘法运算的次数是1750次
2、((AB)(CD)):乘法运算的次数是5300次
3、(((AB)C)D):乘法运算的次数是8000次
4、((A(BC))D):乘法运算的次数是75 500次。
5、(A((BC)D)):乘法运算的次数是31 000次
相乘的顺序不一样,要进行的乘法运算总数也有很大差异。那么,要如何构建一个算法,求出少的乘法运算操作次数?矩阵链相乘的算法如下:
function matrixChainOrder(p, n) { var i, j, k, l, q, m = [], s=[]; for (i = 1; i <= n; i++){ m[i] = []; m[i][i] = 0; } for (i = 0; i <= n; i++){ //to help printing the optimal solution s[i] = []; //auxiliary for (j=0; j<=n; j++){ s[i][j] = 0; } } for (l=2; l<n; l++) { for (i=1; i<=n-l+1; i++) { j = i+l-1; m[i][j] = Number.MAX_SAFE_INTEGER; for (k=i; k<=j-1; k++) { // q = cost/scalar multiplications q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j]; //{1} if (q < m[i][j]){ m[i][j] = q; s[i][j]=k; // s[i,j] = Second auxiliary table that stores k } } } } console.log(m); console.log(s); printOptimalParenthesis(s, 1, n-1); return m[1][n-1]; } function printOptimalParenthesis(s, i, j){ if(i == j) { console.log("A[" + i + "]"); } else { console.log("("); printOptimalParenthesis(s, i, s[i][j]); printOptimalParenthesis(s, s[i][j] + 1, j); console.log(")"); } }
整个算法中重要的是行{1},神奇之处全都在这一行。它计算了给定括号顺序的乘法运算次数,并将值保存在辅助矩阵m中
执行修改后的算法,也能得到括号的最佳顺序(A[1](A[2](A[3]A[4]))),并可以转化为 (A(B(CD)))
贪心算法
贪心算法遵循一种近似解决问题的技术,期盼通过每个阶段的局部最优选择(当前好的解),从而达到全局的最优(全局最优解)。它不像动态规划算法那样计算更大的格局
【最少硬币找零问题】
最少硬币找零问题也能用贪心算法解决。大部分情况下的结果是最优的,不过对有些面额而言,结果不会是优的
function MinCoinChange(coins){ var coins = coins; //{1} this.makeChange = function(amount) { var change = [], total = 0; for (var i=coins.length; i>=0; i--){ //{2} var coin = coins[i]; while (total + coin <= amount) { //{3} change.push(coin); //{4} total += coin; //{5} } } return change; }; }
和动态规划方法相似, 我们传递面额参数,实例化MinCoinChange(行{1})。对每个面额(行{2}——从大到小),把它的值和total相加后,total需要小于amount(行{3})。我们会将当前面额coin添加到结果中(行{4}),也会将它和total相加(行{5})
这个解法很简单。从大面额的硬币开始,拿尽可能多的这种硬币找零。当无法再拿更多这种价值的硬币时,开始拿第二大价值的硬币,依次继续
用和DP方法同样的测试代码测试:
var minCoinChange = new MinCoinChange([1, 5, 10, 25]); console.log(minCoinChange.makeChange(36));
结果依然是[25, 10, 1],和用DP得到的一样。下图阐释了算法的执行过程:
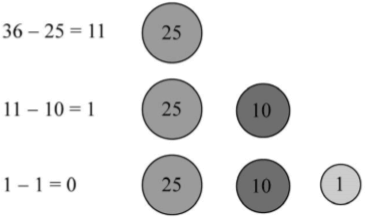
然而,如果用[1, 3, 4]面额执行贪心算法,会得到结果[4, 1, 1]。如果用动态规划的解法,会得到优的结果[3, 3]
比起动态规划算法而言,贪心算法更简单、更快。然而,如我们所见,它并不总是得到优答案。但是综合来看,它相对执行时间来说,输出了一个可以接受的解
【分数背包问题】
求解分数背包问题的算法与动态规划版本稍有不同。在0-1背包问题中,只能向背包里装入完整的物品,而在分数背包问题中,我们可以装入分数的物品。我们用前面用过的例子来比较两者的差异,如下所示:
物品 重量 价值 1 2 3 2 3 4 3 4 5
在动态规划的例子里,考虑背包能够携带的重量只有5。而在这个例子里,我们可以说最佳解决方案是往背包里装入物品1和物品2,总重量为5,总价值为7
如果在分数背包问题中考虑相同的容量,得到的结果是一样的。因此,我们考虑容量为6的情况
在这种情况下,解决方案是装入物品1和物品2,还有25%的物品3。这样,重量为6的物品总价值为8.25
function knapSack(capacity, values, weights) { var n = values.length, load = 0, i = 0, val = 0; for (i = 0; i < n && load < capacity; i++) { //{1} if (weights[i] <= (capacity - load)) { //{2} val += values[i]; load += weights[i]; } else { var r = (capacity - load) / weights[i]; //{3} val += r * values[i]; load += weights[i]; } } return w; }
行{1}:总重量少于背包容量,继续迭代,装入物品
行{2}:如果物品可以完整地装入背包,就将其价值和重量分别计入背包已装入物品的总价值(val)和总重量(load)
行{3}:如果物品不能完整地装入背包,计算能够装入部分的比例(r)
如果在0-1背包问题中考虑同样的容量6,我们就会看到,物品1和物品3组成了解决方案。在这种情况下,对同一个问题应用不同的解决方法,会得到两种不同的结果