hdu 1568 Fibonacci

Posted 2020-06-09

Fibonacci

Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 4267 Accepted Submission(s): 1974

Problem Description

2007年到来了。经过2006年一年的修炼，数学神童zouyu终于把0到100000000的Fibonacci数列
(f[0]=0,f[1]=1;f[i] = f[i-1]+f[i-2](i>=2))的值全部给背了下来。
接下来，CodeStar决定要考考他，于是每问他一个数字，他就要把答案说出来，不过有的数字太长了。所以规定超过4位的只要说出前4位就可以了，可是CodeStar自己又记不住。于是他决定编写一个程序来测验zouyu说的是否正确。

 

 

Input

输入若干数字n(0 <= n <= 100000000)，每个数字一行。读到文件尾。

 

 

Output

输出f[n]的前4个数字（若不足4个数字，就全部输出）。

 

 

Sample Input

0

1

2

3

4

5

35

36

37

38

39

40

 

 

Sample Output

0

1

1

2

3

5

9227

1493

2415

3908

6324

1023

 

 

Author

daringQQ

 

 

Source

Happy 2007

 

 

Recommend

8600 | We have carefully selected several similar problems for you: 1788 1787 1047 1573 3641

 

数学题，，看了别人的博客，自己完全想不到，，好可怕~

 

先看对数的性质,loga(b^c)=c*loga(b),loga(b*c)=loga(b)+loga(c);
假设给出一个数10234432,那么log10(10234432)=log10(1.0234432*10^7)=log10(1.0234432)+7;

log10(1.0234432)就是log10(10234432)的小数部分.

log10(1.0234432)=0.010063744
10^0.010063744=1.023443198
那么要取几位就很明显了吧~
先取对数(对10取),然后得到结果的小数部分bit,pow(10.0,bit)以后如果答案还是<1000那么就一直乘10。
注意偶先处理了0~20项是为了方便处理

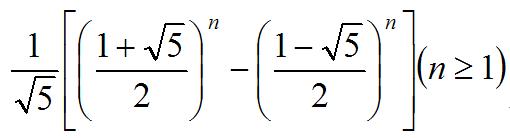
取完对数

 

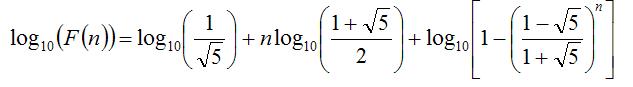
log10(an)=-0.5*log10(5.0)+((double)n)*log(f)/log(10.0)+log10(1-((1-√5)/(1+√5))^n)其中f=(sqrt(5.0)+1.0)/2.0;
log10(1-((1-√5)/(1+√5))^n)->0
所以可以写成log10(an)=-0.5*log10(5.0)+((double)n)*log(f)/log(10.0);
最后取其小数部分。

 

附上代码：

 

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <cmath>
 5 using namespace std;
 6 int d[40]={0,1};
 7 int main()
 8 {
 9     int i,j;
10     for(i=2;i<=20;i++)
11     d[i]=d[i-1]+d[i-2];
12     int n,ans;
13     double p,f;
14     f=(1.0+sqrt(5.0))/2.0;
15     while(~scanf("%d",&n))
16     {
17         if(n<21)
18         {
19             printf("%d\n",d[n]);
20             continue;
21         }
22         p=-0.5*log10(5.0)+n*1.0*log(f)/log(10.0);
23         p=p-(int)p;
24         p=pow(10.0,p);
25         while(p<1000)
26         p*=10;
27         printf("%d\n",(int)p);
28     }
29     return 0;
30 }