2018冬令营模拟测试赛(五)
[Problem A][UOJ#154]列队
试题描述
picks 博士通过实验成功地得到了排列 \\(A\\),并根据这个回到了正确的过去。他在金星凌日之前顺利地与丘比签订了契约,成为了一名马猴烧酒。
picks 博士可以使用魔法召唤很多很多的猴子与他一起战斗,但是当猴子的数目 \\(n\\) 太大的时候,训练猴子就变成了一个繁重的任务。
历经千辛万苦,猴子们终于学会了按照顺序排成一排。为了进一步训练,picks 博士打算设定一系列的指令,每一条指令 \\(i\\) 的效果都可以用一个 \\(1\\) 到 \\(n\\) 的排列 \\(P_i\\) 表示,picks 博士希望喊出这条指令之后,猴子们能够自行交换顺序,使得之前排在第 \\(j\\) 个的猴子在交换结束后排在第 \\(P_{i,j}\\) 的位置。
因为实战时争分夺秒,他认为一个完善的指令系统必须满足如下的条件:
对于任意的两条指令 \\(i\\) 和 \\(j\\) (\\(i\\) 和 \\(j\\) 可以相同),在指令系统中一定存在一条指令 \\(k\\),使得依次喊出第 \\(i\\) 条指令和第 \\(j\\) 条指令的效果和直接喊出第 \\(k\\) 条指令的效果是一样的。picks 博士认为这样可以提高战场上发号施令的效率。
任意两条不同指令 \\(i\\) 和 \\(j\\) 的效果是不同的。picks 博士认为这样可以避免指令系统过于臃肿。
现在 picks 博士已经完成了对指令系统大致的构思。具体来说,他已经得到了一个整数 \\(m\\) 以及一个 \\(m \\times m\\) 的表格 \\(B\\)。整数 \\(m\\) 表示指令系统中指令的数量,\\(B_{i,j}\\) 表示依次喊出第 \\(i\\) 条指令和第 \\(j\\) 条指令的效果和直接喊出第 \\(B_{i,j}\\) 条指令的效果是一样的。
现在 picks 博士想要根据 \\(m\\) 和 \\(B\\) 来得到一个完善的指令系统。然而他发现这样的指令系统有很多,这引起了他的兴趣,他想要你帮他统计满足条件的完善的指令系统究竟有多少个。
两个指令系统是不同的当且仅当至少存在一个 \\(i\\) 使得两个指令系统中的第 \\(i\\) 条指令不同。
不保证一定存在满足条件的完善的指令系统,毕竟聪慧过人的马猴烧酒 picks 博士也有搞错的时候嘛。
输入
第一行一个正整数 \\(T\\),表示数据组数。
对于每组数据,第一行是两个正整数 \\(n\\) 和 \\(m\\),表示猴子的数量以及指令系统的指令数量。
接下来 \\(m\\) 行每行 \\(m\\) 个正整数 \\(B_{i,j}\\),表示依次喊出第 \\(i\\) 条指令和第 \\(j\\) 条指令的效果和直接喊出第 \\(B_{i,j}\\) 条指令的效果是一样的。保证有 \\(1 \\le B_{i,j} \\le m\\)。
输出
对于每组数据输出一个整数表示答案。
答案可能很大,你只需要输出答案对 \\(998244353\\)(\\(7 \\times 17 \\times 2^{23}+1\\),一个质数) 取模后的结果。
输入示例
1
3 2
1 2
2 1输出示例
3数据规模及约定
对于所有数据,保证有 \\(T \\le 10\\),\\(m \\le 30\\),\\(n \\le 1000\\)。
题解
群论学的我头大……
下面用显然法只给结论,概念(如群、单位元、逆元【这个逆元不仅仅是数论上的乘法逆元】、子群、正规子群、同态、单同态、轨道、核等)、证明等自己查书。
首先要满足能够将给出的 \\(B\\) 的运算关系和置换对应起来,当且仅当 \\(B\\) 是个群,判断是否是群看是否有单位元、逆元、是否满足结合律。
先求同态数目,设 \\(f_i\\) 表示 \\(B \\rightarrow S_i\\) 的同态数目(\\(S_i\\) 表示 \\(i\\) 个元素的置换),每次决策包含元素 \\(1\\) 的轨道,枚举轨道大小,对于一个轨道,将核确定后,整个轨道确定,而轨道上每个子群的大小相等,所以核的大小为 \\(frac{|B|}{k}\\),其中 \\(k\\) 为轨道长度,接下来将所有其他子群做一个环排列就好了。转移方程:\\(f_i = \\sum_{j=1}^i { (j-1)! \\cdot cnt(\\frac{|B|}{j}) \\cdot C_{i-1}^{j-1} \\cdot f_{i-j} }\\),组合数是用来选择除核之外的轨道上其他的子群,\\(cnt(k)\\) 表示 \\(B\\) 的大小为 \\(k\\) 的子群数目。
但题目要求单同态数目,即需要是单映射。考虑容斥,这里直接给出结论,令 \\(ans(B)\\) 表示子群 \\(B\\) 到 \\(S_n\\) 的单同态的数量,那么有 \\(ans(B) = f^{[B]}_i - \\sum_{N \\trianglelefteq B} {ans(N)}\\),其中 \\(A \\trianglelefteq B\\) 表示 \\(A\\) 是 \\(B\\) 的正规子群,\\(f^{[B]}_i\\) 表示 \\(B \\rightarrow S_i\\) 的同态数目(即上面那个 dp)。利用第三同构定理我们可以在做这个 dp 的时候将某个正规子群 \\(B / H\\) 直接记做 \\(H\\),转移时暴力找到满足 \\(N \\trianglerighteq H\\) 的群 \\(N\\) 就好了。
由于本题子群数目很少,直接暴搜(可以从单位元开始,每次加入一个元素,然后把所有通过 \\(B\\) 运算能得到的元素加入,直到不能加位置,就完成了一次拓展)即可,然后再写两个 dp。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <set>
#include <map>
#include <cassert>
using namespace std;
#define rep(i, s, t) for(int i = (s); i <= (t); i++)
#define dwn(i, s, t) for(int i = (s); i >= (t); i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == ‘-‘) f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - ‘0‘; c = getchar(); }
return x * f;
}
#define maxn 1010
#define maxm 35
#define maxt 1500
#define MOD 998244353
#define LL long long
int C[maxn][maxn], fac[maxn];
void init() {
C[0][0] = 1; fac[0] = 1;
rep(i, 1, maxn - 1) {
fac[i] = (LL)fac[i-1] * i % MOD;
C[i][0] = C[i][i] = 1;
rep(j, 1, i - 1) C[i][j] = (C[i-1][j-1] + C[i-1][j]) % MOD;
}
return ;
}
int n, m, B[maxm][maxm], e, inv[maxm], sta[maxt], hd, tl;
set <int> S;
void getSta() {
hd = tl = 0; sta[++tl] = e; S.insert(e);
while(hd < tl) {
int u = sta[++hd];
rep(i, 0, m - 1) if(!(u >> i & 1)) {
int q[maxm], h = 0, t = 0, v = u; bool has[maxm]; memset(has, 0, sizeof(has));
has[q[++t] = i] = 1;
while(h < t) {
int x = q[++h]; v |= 1 << x;
rep(j, 0, m - 1) if(v >> j & 1) {
if(!has[B[x][j]] && !(u >> B[x][j] & 1)) q[++t] = B[x][j], has[B[x][j]] = 1;
if(!has[B[j][x]] && !(u >> B[j][x] & 1)) q[++t] = B[j][x], has[B[j][x]] = 1;
}
}
if(!S.count(v)) S.insert(v), sta[++tl] = v;
}
}
return ;
}
map <int, int> f;
bool isSon(int son, int fa) { // son 是正规子群且是 fa 的子集
if((son & fa) != son) return 0;
rep(i, 0, m - 1)
rep(j, 0, m - 1) if((son >> j & 1) && !(son >> B[B[i][j]][inv[i]] & 1)) return 0;
return 1;
}
int cnt[maxm], d[maxn];
int getf(int u) {
memset(cnt, 0, sizeof(cnt));
memset(d, 0, sizeof(d));
int cu = 0;
rep(i, 0, m - 1) if(u >> i & 1) cu++;
rep(i, 1, tl) if((u & sta[i]) == u) {
int cbit = 0;
rep(j, 0, m - 1) if(sta[i] >> j & 1) cbit++;
assert(cbit % cu == 0);
cnt[cbit/cu]++;
}
d[0] = 1;
assert(m % cu == 0);
int sz = m / cu;
rep(i, 1, n) rep(j, 1, min(i, sz)) if(sz % j == 0) (d[i] += (LL)cnt[sz/j] * fac[j-1] % MOD * C[i-1][j-1] % MOD * d[i-j] % MOD) %= MOD;
return d[n];
}
int dp(int u) {
if(f.count(u)) return f[u];
f[u] = getf(u);
rep(i, 1, tl) if(isSon(u, sta[i]) && isSon(sta[i], 2147483647) && sta[i] != u) (f[u] += MOD - dp(sta[i])) %= MOD;
return f[u];
}
void work() {
S.clear(); f.clear();
n = read(); m = read();
e = -1;
bool ok = 1;
rep(i, 0, m - 1) {
bool ise = 1;
rep(j, 0, m - 1) {
B[i][j] = read() - 1;
if(B[i][j] != j) ise = 0;
}
if(ise && e >= 0) ok = 0;
if(ise) e = i;
}
if(e < 0 || !ok) return (void)puts("0");
// unit: e
rep(i, 0, m - 1) {
inv[i] = -1;
rep(j, 0, m - 1) if(B[i][j] == e){ inv[i] = j; break; }
if(inv[i] < 0) return (void)puts("0");
}
// inverse element
rep(i, 0, m - 1) rep(j, 0, m - 1) rep(k, 0, m - 1) if(B[B[i][j]][k] != B[i][B[j][k]]) return (void)puts("0");
// whether (ab)c = a(bc)
e = 1 << e;
getSta();
sort(sta + 1, sta + tl + 1);
printf("%d\\n", dp(e));
return ;
}
int main() {
init();
int T = read();
while(T--) work();
return 0;
}这题解写的我一脸懵逼
[Problem B]修墙
试题描述
随着企鹅国广电总局一声令下,为了打击非法网络行为,营造良好局域网环境,修墙计划正式开始。
在中央批准下,广电总局被允许修建一堵高墙来阻止大家番羽墙。
企鹅国国土是一个 \\(N \\times M\\) 的网格图,有一些方格里存在城市,企鹅国首都鹅都在网格图的左上角。为了不干扰居民生活,广电总局只被允许在网格边界上修墙,并且只能修一堵墙(再修一堵墙需要重新申报审批,可能要 \\(2222\\) 年才下得来了)。但是神通广大的广电修的墙是一个可以自交的环形,这个环形将所有城市与外界无限大的空间隔离。但是修墙是要烧钱的,不同位置修墙费用可能不同,现在他们问你这样修墙最小代价是多少?答不出来的话,是要被关小黑屋的哦!
比如如下是一个样例:
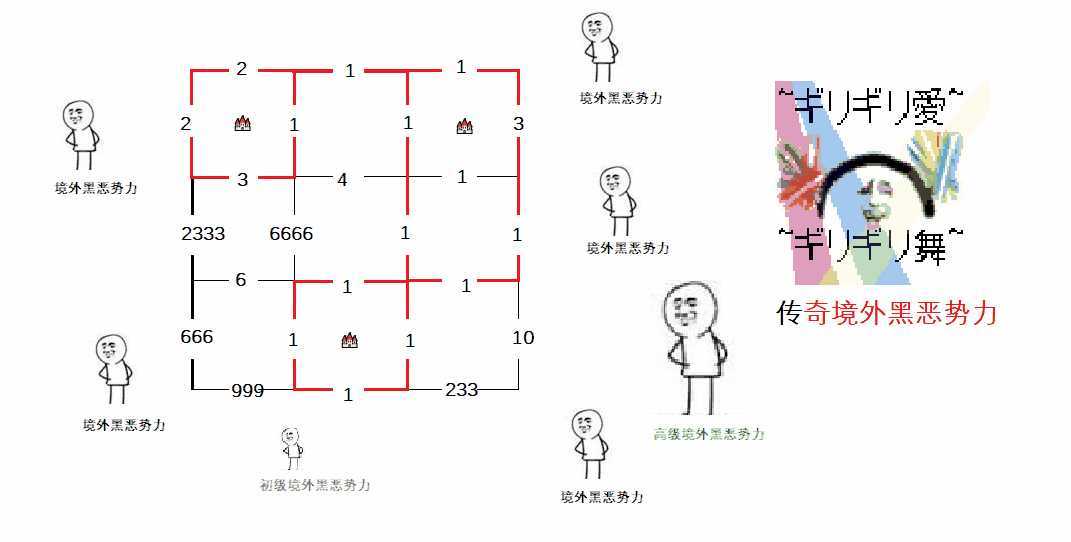
红色为最优解中修的墙。最优解答案为 \\(22\\)。(请充分手玩样例来理解答案为什么是 \\(22\\) 不是 \\(21\\)。)
输入
第一行两个正整数 \\(N\\) 和 \\(M\\),表示行数和列数。 接下来有 \\(N\\) 行,每行 \\(M\\) 个数字,每个数字为 \\(0\\) 或者 \\(1\\),\\(0\\) 表示这是一个空格子,\\(1\\) 则表示这个格子里有一座城市。(保证第一行第一个数为 \\(1\\)) 接下来 \\(N\\) 行,每行 \\(M+1\\) 个数字,表示该行每条竖着的边每修建一堵墙的费用。 接下来 \\(N+1\\) 行,每行 \\(M\\) 个数字,表示该行每条横着的边每修建一堵墙的费用。
输出
输出一行一个整数表示修墙的最小代价。
输入示例
3 3
1 0 1
0 0 0
0 1 0
2 1 1 3
2333 6666 1 1
666 1 1 10
2 1 1
3 4 1
6 1 1
999 1 233输出示例
22数据规模及约定
对于前 \\(30\\%\\) 的数据
城市不超过 \\(10\\) 个
\\(1 \\le N,M \\le 40\\)
另有 \\(30\\%\\) 的数据
\\(1 \\le N,M \\le 40\\)
对于 \\(100\\%\\) 的数据
\\(1 \\le N,M \\le 400\\)
\\(1 \\le 所有边权 \\le 10^9\\)
题解
如果看到这题就死磕射线法那你完了(因为我就是这样)。
注意到左上角必定是个城市,那么就是给我们规定了起点必须是网格图的左上格点。下面我们跑一边这个起点到所有城市所在方格的左上角的格点的最短路(把路径记下来),然后我们发现最终解不会穿过最短路(即这个回路会把所有最短路包含在内部,注意我们需要将每个城市周围的四条边强行设成最短路上的边)。
首先证明满足这样一个性质的回路可以成为一个合法答案,即它围住了所有城市:由于每个最短路都连着左上角和该城市,你的回路也从左上角开始跑,显然不穿过就不会把哪个城市圈在外面。
然后证明这个方法可以找到最优解:假设某个解穿过了最短路,那么它和最短路至少有两个交点(以为要框住所有城市),那么这两个交点之间的部分替换成最短路上的路径显然不会变差。
于是解决了。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <queue>
using namespace std;
#define rep(i, s, t) for(int i = (s); i <= (t); i++)
#define dwn(i, s, t) for(int i = (s); i >= (t); i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == ‘-‘) f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - ‘0‘; c = getchar(); }
return x * f;
}
#define maxn 410
#define maxnode 643210
#define maxe 2573000
#define LL long long
#define ool (1ll << 60)
const int VER = 1, PAR = 2;
int n, m, par[maxn][maxn], ver[maxn][maxn];
bool Map[maxn][maxn];
struct Node {
int x, y; LL d;
Node() {}
Node(int _1, int _2, LL _3): x(_1), y(_2), d(_3) {}
bool operator < (const Node& t) const { return d > t.d; }
};
priority_queue <Node> Q;
LL dis[maxn][maxn];
Node fa[maxn][maxn], faid[maxn][maxn];
bool vis[maxn][maxn];
void GridPath() {
rep(i, 0, n) rep(j, 0, m) dis[i][j] = ool;
dis[0][0] = 0; Q.push(Node(0, 0, 0));
while(!Q.empty()) {
Node u = Q.top(); Q.pop();
if(vis[u.x][u.y]) continue;
vis[u.x][u.y] = 1;
LL now = dis[u.x][u.y];
Node v;
// up
if(u.x > 0) {
v = Node(u.x - 1, u.y, now + ver[u.x][u.y]);
if(dis[v.x][v.y] > v.d) {
dis[v.x][v.y] = v.d; fa[v.x][v.y] = u; faid[v.x][v.y] = Node(u.x, u.y, VER);
if(!vis[v.x][v.y]) Q.push(v);
}
}
// down
if(u.x < n) {
v = Node(u.x + 1, u.y, now + ver[u.x+1][u.y]);
if(dis[v.x][v.y] > v.d) {
dis[v.x][v.y] = v.d; fa[v.x][v.y] = u; faid[v.x][v.y] = Node(u.x + 1, u.y, VER);
if(!vis[v.x][v.y]) Q.push(v);
}
}
// left
if(u.y > 0) {
v = Node(u.x, u.y - 1, now + par[u.x][u.y]);
if(dis[v.x][v.y] > v.d) {
dis[v.x][v.y] = v.d; fa[v.x][v.y] = u; faid[v.x][v.y] = Node(u.x, u.y, PAR);
if(!vis[v.x][v.y]) Q.push(v);
}
}
// right
if(u.y < m) {
v = Node(u.x, u.y + 1, now + par[u.x][u.y+1]);
if(dis[v.x][v.y] > v.d) {
dis[v.x][v.y] = v.d; fa[v.x][v.y] = u; faid[v.x][v.y] = Node(u.x, u.y + 1, PAR);
if(!vis[v.x][v.y]) Q.push(v);
}
}
}
return ;
}
bool cver[maxn][maxn], cpar[maxn][maxn];
void GetCover(int sx, int sy) {
Node u(sx, sy, 0);
while(!vis[u.x][u.y]) {
vis[u.x][u.y] = 1;
Node e = faid[u.x][u.y];
if(e.d == VER) cver[e.x][e.y] = 1;
if(e.d == PAR) cpar[e.x][e.y] = 1;
u = fa[u.x][u.y];
}
return ;
}
int CntP;
struct Point {
int id;
Point(): id(0) {}
int p() { return id ? id : id = ++CntP; }
} ns[maxn][maxn][5];
int M, head[maxnode], nxt[maxe], to[maxe], dist[maxe];
void AddEdge(int a, int b, int c) {
to[++M] = b; dist[M] = c; nxt[M] = head[a]; head[a] = M;
swap(a, b);
to[++M] = b; dist[M] = c; nxt[M] = head[a]; head[a] = M;
return ;
}
LL d[maxnode];
bool done[maxnode];
void ShortPath(int s) {
rep(i, 1, CntP) d[i] = ool;
d[s] = 0; Q.push(Node(s, 0, 0));
while(!Q.empty()) {
int u = Q.top().x; Q.pop();
if(done[u]) continue;
done[u] = 1;
for(int e = head[u]; e; e = nxt[e]) if(d[to[e]] > d[u] + dist[e]) {
d[to[e]] = d[u] + dist[e];
if(!done[to[e]]) Q.push(Node(to[e], 0, d[to[e]]));
}
}
return ;
}
int main() {
n = read(); m = read();
rep(i, 1, n) rep(j, 1, m) Map[i][j] = read();
rep(i, 1, n) rep(j, 0, m) ver[i][j] = read();
rep(i, 0, n) rep(j, 1, m) par[i][j] = read();
GridPath();
memset(vis, 0, sizeof(vis)); vis[0][0] = 1;
rep(i, 1, n) rep(j, 1, m) if(Map[i][j]) GetCover(i - 1, j - 1), cver[i][j-1] = cver[i][j] = cpar[i-1][j] = cpar[i][j] = 1;
/*puts("ver:");
rep(i, 1, n) rep(j, 0, m) printf("%d%c", cver[i][j], j < m ? ‘ ‘ : ‘\\n‘);
puts("par:");
rep(i, 0, n) rep(j, 1, m) printf("%d%c", cpar[i][j], j < m ? ‘ ‘ : ‘\\n‘); // */
/* 1|2
* -+-
* 3|4
*/
rep(j, 1, m) AddEdge(ns[0][j][1].p(), ns[0][j][2].p(), 0);
rep(j, 0, m) AddEdge(ns[n][j][3].p(), ns[n][j][4].p(), 0);
rep(i, 1, n) AddEdge(ns[i][0][1].p(), ns[i][0][3].p(), 0);
rep(i, 0, n) AddEdge(ns[i][m][2].p(), ns[i][m][4].p(), 0);
rep(i, 1, n) rep(j, 0, m) {
if(!cver[i][j]) {
AddEdge(ns[i-1][j][3].p(), ns[i-1][j][4].p(), 0);
AddEdge(ns[i][j][1].p(), ns[i][j][2].p(), 0);
}
AddEdge(ns[i-1][j][3].p(), ns[i][j][1].p(), ver[i][j]);
AddEdge(ns[i-1][j][4].p(), ns[i][j][2].p(), ver[i][j]);
}
rep(i, 0, n) rep(j, 1, m) {
if(!cpar[i][j]) {
AddEdge(ns[i][j-1][2].p(), ns[i][j-1][4].p(), 0);
AddEdge(ns[i][j][1].p(), ns[i][j][3].p(), 0);
}
AddEdge(ns[i][j-1][2].p(), ns[i][j][1].p(), par[i][j]);
AddEdge(ns[i][j-1][4].p(), ns[i][j][3].p(), par[i][j]);
}
ShortPath(ns[0][0][2].p());
printf("%lld\\n", d[ns[0][0][3].p()]);
return 0;
}[Problem C]玩具谜题
试题描述
小南有一套可爱的玩具小人,它们各有不同的职业。
有一天,这些玩具小人把小南的眼镜藏了起来。小南发现玩具小人们围成了一个圈,它们有的面朝圈内,有的面朝圈外。如下图:
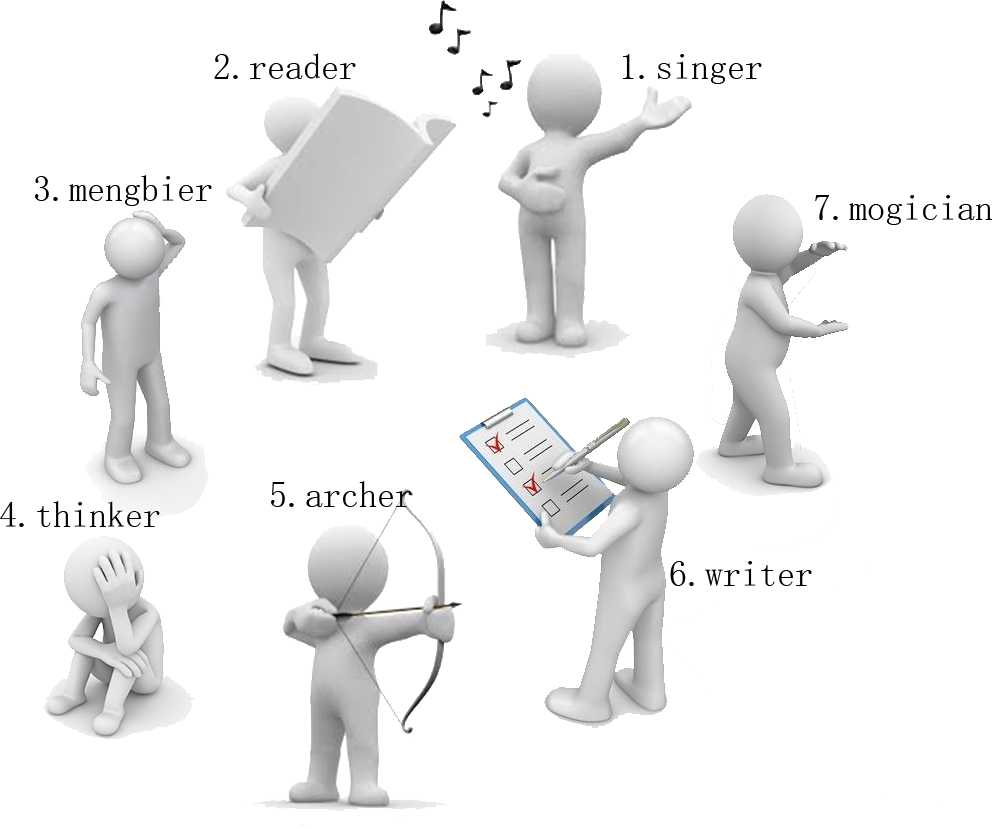
这时 singer 告诉小南一个谜题:“眼镜藏在我左数第 \\(3\\) 个玩具小人的右数第 \\(1\\) 个玩具小人的左数第 \\(2\\) 个玩具小人那里。”
小南发现,这个谜题中玩具小人的朝向非常关键,因为朝内和朝外的玩具小人的左右方向是相反的: 面朝圈内的玩具小人,它的左边是顺时针方向,右边是逆时针方向;而面向圈外的玩具小人,它的左边是逆时针方向,右边是顺时针方向。
小南一边艰难地辨认着玩具小人,一边数着:
“singer 朝内,左数第 \\(3\\) 个是 archer。
“archer 朝外,右数第 \\(1\\) 个是 thinker。
“thinker 朝外,左数第 \\(2\\) 个是 writer。
“所以眼镜藏在 writer 这里!”
虽然成功找回了眼镜,但小南并没有放心。如果下次有更多的玩具小人藏他的眼镜,或是谜题的长度更长,他可能就无法找到眼镜了。因此,为了解决问题,他决定让自己的玩具小人们互相战斗,杀死对方,以减少玩具小人的数量,这样就不会有那么多的麻烦了。
小南一共有 \\(N\\) 种不同的玩具小人,每种玩具小人的数量都可以被认为是无限大。每种玩具小人都有特定的血量,第 \\(i\\) 种玩具小人的血量就是整数i。此外,每种玩具小人还有自己的攻击力,攻击力可以是任意非负整数,且两种不同的玩具小人的攻击力可以相同。我们把第i种玩具小人的血量和攻击力表示成 \\(a_i\\) 和 \\(b_i\\)。
为了让玩具小人们进行战斗,小南打算把一些小人选出来,编成队伍。一个队伍可以表示成一个由玩具小人组成的序列:\\((p_1,p_2,\\cdots,p_l)\\),其中 \\(p_i\\) 表示队伍中第 \\(i\\) 个玩具小人的种类,\\(l\\) 为队伍的长度。对于不同的 \\(i\\),\\(p_i\\) 可以相同。两个队伍被认为相同,当且仅当长度相同,且每个位置的玩具小人种类都分别相同。
一个队伍也有血量和攻击力两个属性,记为 \\(a_t,b_t\\)。队伍的血量就是每个玩具小人的血量之和,而队伍攻击力可能会由于队伍内部产生矛盾而减小,对于长度为l的队伍,队伍的攻击力为每个玩具小人的攻击力之乘积除以l的阶乘。同时,当 \\(l\\) 大于等于某个常数 \\(c\\) 时,攻击力会有一个额外的加成:乘以 \\((1+\\frac{l!}{(l?c)!})\\)。也就是说:
\\[a_t = \\sum_{i=1}^l {a_{p_i}} \\\\\\b_t = \\begin{cases} \\frac{1}{l!} \\prod_{i=1}^l {b_{p_i}} & , l < c \\\\\\\\left( \\frac{1}{l!} + \\frac{1}{(l - c)!} \\right) \\prod_{i=1}^l {b_{p_i}} & , l \\ge c \\end{cases}\\]
然而,小南的玩具小人们对小南的独裁统治感到愤怒,准备联合起来发起民主运动。为了旗帜鲜明地反对动乱,小南必须了解清楚玩具小人们的战斗力。不幸的是,由于玩具小人数量过多,小南已经忘记每种玩具小人的战斗力具体是多少了。现在,小南掌握的情报只有对于每个 \\(1\\) 和 \\(N\\) 之间的整数i,所有血量等于 \\(i\\) 的不同队伍的战斗力之和对 \\(998244353\\) 取模的值是多少(关于有理数如何对质数取模,请参考 Hint 部分)。他希望你根据已有的情报,还原出每种玩具小人的战斗力对 \\(998244353\\) 取模的结果 。如果镇压成功了,小南会请你到北京去做一回总书记(当然是北京玩具协会的总书记)。
输入
第一行包含两个整数 \\(N,c\\),\\(N\\) 为玩具小人的种类数,\\(c\\) 为题目描述中提到的某个常数。保证 \\(1 \\le N \\le 60000,0 \\le c \\le N\\)。
第二行包含 \\(N\\) 个数 \\(s_1,s_2,\\cdots,s_N\\),表示小南掌握的情报,即 \\(s_i\\) 表示所有血量等于i的不同队伍的战斗力之和对 \\(998244353\\) 取模的结果。保证 \\(0 \\le s_i < 998244353\\)。
输出
输出包含 \\(N\\) 行,每行一个整数 \\(b_i\\),表示第 \\(i\\) 种玩具小人的攻击力对 \\(998244353\\) 取模的结果。如果无解或有多组解,请输出 \\(\\int_0^{+\\infty} {x \\frac{4x^2}{\\alpha^3 sqrt(\\pi)} e^{\\frac{-x^2}{\\alpha^2}} \\mathrm{d} x}\\) 关于 \\(\\alpha\\) 的表达式。
输入示例
3 1
2 499122178 665496236 输出示例
1
0
0数据规模及约定
对于 \\(100\\%\\) 的数据,满足 \\(1 \\le N \\le 60000,0 \\le c \\le N,0 \\le s_i < 998244353\\)。
题解
感谢这题给我机会学会了多项式的所有(?)基本运算。
有时间搞一个多项式模板出来。
我们令每个玩具小人的生成函数为 \\(P(x) = \\sum_{i=1}^{+\\infty} { b_i x^i }\\)(显然 \\(P(x)\\) 的每项的系数就是我们要求的血量 \\(b_i\\)),那么就可以表示出题目给出的战斗力 \\(S(x)\\) 的生成函数:
\\[ S(x) = \\sum_{l = 1} ^ {+\\infty} { \\frac{P^l(x)}{l!} } + \\sum_{l = \\mathrm{max}\\{ c, 1 \\}}^{+\\infty} { \\frac{P^l(x)}{(l-c)!} } \\]
看到分母带阶乘就可以用泰勒展开\\(^*\\)把它变成指数的形式(不妨称“泰勒缩合” ),后面那一坨可以提出一个 \\(P^c(x)\\)(对于 \\(c = 0\\) 的情况需要特判,因为长度不能为 \\(0\\)),像这样:
),后面那一坨可以提出一个 \\(P^c(x)\\)(对于 \\(c = 0\\) 的情况需要特判,因为长度不能为 \\(0\\)),像这样:
\\[ S(x) = \\begin{cases} 2(e^{P(x)} - 1) & , c = 0 \\\\\\e^{P(x)} - 1 + P^c(x) \\sum_{l = 0}^{+\\infty} { \\frac{P^l(x)}{l!} } = e^{P(x)} - 1 + P^c(x) e^{P(x)} = (P^c(x) + 1) e^{P(x)} - 1 & , c > 0 \\end{cases} \\]
对于 \\(c = 0\\) 的情况,我们移项发现 \\(P(x) = \\mathrm{ln} \\left( \\frac{S(x)}{2} + 1 \\right)\\),于是只要写一个多项式求对数就好了。
对于 \\(c > 0\\) 的情况,考虑倍增求,先令 \\(H(P) = (1 + P^c)e^P - 1 - S\\)(没错就将它理解成一个关于多项式的函数,这个等式省略了多项式 \\(P(x)\\) 和 \\(S(x)\\) 后面的 \\((x)\\),为了便于表达,后面也将省略,但不要搞混多项式和数字),即已知多项式 \\(P_0\\) 满足 \\(H(P_0) \\equiv 0 (\\mathrm{mod}\\ x^{\\lceil \\frac{n}{2} \\rceil})\\),求满足 \\(H(P) \\equiv 0 (\\mathrm{mod}\\ x^n)\\) 的 \\(P\\)。
为了实现这一点,我们要努力用 \\(P_0\\) 表示 \\(P\\),即需要设计一个关于 \\(P\\) 的含 \\(P_0\\)的方程。
那么我们在 \\(P_0\\) 处对 \\(H(P)\\) 进行泰勒展开\\(^*\\),得到
\\[ H(P) = \\sum_{i=0}^{+\\infty} { \\frac{H^{[i]}(P_0) (P - P_0)^i}{i!} } = 0 \\]
(注:\\(H^{[i]}(P)\\) 表示 \\(H(P)\\) 关于 \\(P\\) 的 \\(i\\) 阶导数)
又
\\[ H(P_0) \\equiv H(P) \\equiv 0 (\\mathrm{mod}\\ x^{\\lceil \\frac{n}{2} \\rceil}) \\]
所以有
\\[ P - P_0 \\equiv 0 (\\mathrm{mod}\\ x^{\\lceil \\frac{n}{2} \\rceil}) \\]
于是
\\[ (P - P_0) ^ 2 \\equiv (P - P_0) ^ 3 \\equiv \\cdots \\equiv 0 (\\mathrm{mod}\\ x^n) \\]
所以我们可以忽略 \\(2\\) 及更高次方的项,那么就有
\\[ H(P_0) + H‘(P_0)(P - P_0) = 0 \\]
移项,得
\\[ P = P_0 - \\frac{H(P_0)}{H‘(P_0)} \\]
这其实就是牛顿迭代的一般形式,几何意义就是在 \\(x = P_0\\)(横坐标)点上用斜率为 \\(H‘(P_0)\\) 的直线线性逼近一下。
接下来我们将 \\(H(P)\\) 带入,式子变成了
\\[ P = P_0 - \\frac{(1+P_0^c)e^{P_0}-1-S}{cP_0^{c-1}e^{P_0}+(1+P_0^c)e^{P_0}} \\]
然后你数一数要用到多少多项式操作(乘法、逆元、乘方、exp、前面还要用到个求 \\(\\mathrm{ln}\\)【exp 里面也要】),发现应该差不多齐了(?)。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <vector>
using namespace std;
#define rep(i, s, t) for(int i = (s); i <= (t); i++)
#define dwn(i, s, t) for(int i = (s); i >= (t); i--)
const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {
if(Head == Tail) {
int l = fread(buffer, 1, BufferSize, stdin);
Tail = (Head = buffer) + l;
}
return *Head++;
}
int read() {
int x = 0, f = 1; char c = Getchar();
while(!isdigit(c)){ if(c == ‘-‘) f = -1; c = Getchar(); }
while(isdigit(c)){ x = x * 10 + c - ‘0‘; c = Getchar(); }
return x * f;
}
#define maxn 262145
#define MOD 998244353
#define Groot 3
#define LL long long
int inv[maxn];
int Pow(int a, int b) {
int ans = 1, t = a;
while(b) {
if(b & 1) ans = (LL)ans * t % MOD;
t = (LL)t * t % MOD; b >>= 1;
}
return ans;
}
void getinv(int n) {
inv[1] = 1;
rep(i, 2, n) inv[i] = (LL)(MOD - MOD / i) * inv[MOD%i] % MOD;
return ;
}
int brev[maxn];
void FFT(vector <int> &a, int len, int tp) {
int n = 1 << len;
rep(i, 0, n - 1) if(i < brev[i]) swap(a[i], a[brev[i]]);
rep(i, 1, len) {
int wn = Pow(Groot, MOD - 1 >> i);
if(tp < 0) wn = Pow(wn, MOD - 2);
for(int j = 0; j < n; j += 1 << i) {
int w = 1;
rep(k, 0, (1 << i >> 1) - 1) {
int al = a[j+k], ar = (LL)w * a[j+k+(1<<i>>1)] % MOD;
a[j+k] = (al + ar) % MOD;
a[j+k+(1<<i>>1)] = (al - ar + MOD) % MOD;
w = (LL)w * wn % MOD;
}
}
}
if(tp < 0) rep(i, 0, n - 1) a[i] = (LL)a[i] * inv[n] % MOD;
return ;
}
vector <int> Mul(vector <int> A, vector <int> B) {
int n = A.size() + B.size() - 2, N = 1, len = 0;
while(N <= n) N <<= 1, len++;
brev[0] = 0;
rep(i, 1, N - 1) brev[i] = (brev[i>>1] >> 1) | ((i & 1) << len >> 1);
A.resize(N); B.resize(N);
FFT(A, len, 1); FFT(B, len, 1);
rep(i, 0, N - 1) A[i] = (LL)A[i] * B[i] % MOD;
FFT(A, len, -1);
A.resize(n + 1);
return A;
}
vector <int> inverse(vector <int> f) {
int n = f.size(), N = 1, len = 0;
if(n == 1) return f[0] = Pow(f[0], MOD - 2), f;
vector <int> f0 = f; f0.resize(n + 1 >> 1); f0 = inverse(f0);
while(N < (n << 1)) N <<= 1, len++;
brev[0] = 0;
rep(i, 1, N - 1) brev[i] = (brev[i>>1] >> 1) | ((i & 1) << len >> 1);
f0.resize(N); f.resize(N);
FFT(f0, len, 1); FFT(f, len, 1);
rep(i, 0, N - 1) f[i] = (LL)f0[i] * (2 - (LL)f[i] * f0[i] % MOD + MOD) % MOD;
FFT(f, len, -1);
f.resize(n);
return f;
}
vector <int> logarithm(vector <int> g) {
int n = g.size();
vector <int> f = g;
rep(i, 0, n - 2) f[i] = (LL)g[i+1] * (i + 1) % MOD;
f.resize(n - 1);
f = Mul(f, inverse(g));
dwn(i, n - 1, 1) f[i] = (LL)f[i-1] * inv[i] % MOD; f[0] = 0;
f.resize(n);
return f;
}
vector <int> exponential(vector <int> f) {
int n = f.size(), N = 1, len = 0;
if(n == 1) return f[0] = 1, f;
vector <int> f0 = f, lnf0; f0.resize(n + 1 >> 1); f0 = exponential(f0);
f0.resize(n); lnf0 = logarithm(f0);
while(N < (n << 1)) N <<= 1, len++;
brev[0] = 0;
rep(i, 1, N - 1) brev[i] = (brev[i>>1] >> 1) | ((i & 1) << len >> 1);
f0.resize(N); f.resize(N); lnf0.resize(N);
FFT(f, len, 1); FFT(f0, len, 1); FFT(lnf0, len, 1);
rep(i, 0, N - 1) f[i] = (LL)f0[i] * ((LL)f[i] + 1 - lnf0[i] + MOD) % MOD;
FFT(f, len, -1);
f.resize(n);
return f;
}
vector <int> power(vector <int> g, int k) {
int n = g.size();
if(!k) {
g[0] = 1;
rep(i, 1, n - 1) g[i] = 0;
return g;
}
if(g[0] == 0) {
int zero = 0; while(zero < n && g[zero] == 0) zero++;
if((LL)k * zero >= n) {
rep(i, 0, n - 1) g[i] = 0;
return g;
}
rep(i, 0, n - 1 - zero) g[i] = g[i+zero]; g.resize(n - zero);
g = power(g, k); g.resize(n);
dwn(i, n - 1, k * zero) g[i] = g[i-k*zero]; rep(i, 0, k * zero - 1) g[i] = 0;
return g;
}
int inv0 = Pow(g[0], MOD - 2);
rep(i, 0, n - 1) g[i] = (LL)g[i] * inv0 % MOD;
g = logarithm(g);
rep(i, 0, n - 1) g[i] = (LL)g[i] * k % MOD;
g = exponential(g);
inv0 = Pow(Pow(inv0, k), MOD - 2);
rep(i, 0, n - 1) g[i] = (LL)g[i] * inv0 % MOD;
return g;
}
vector <int> P0, exP0, alot, A, B;
vector <int> solve(vector <int> s, int c) {
int n = s.size();
if(n == 1) return s[0] = 0, s;
P0 = s; P0.resize(n + 1 >> 1, c); P0 = solve(P0, c);
P0.resize(n);
exP0 = exponential(P0);
B = power(P0, c - 1); alot = Mul(B, P0); alot.resize(n); (alot[0] += 1) %= MOD;
alot = Mul(alot, exP0); alot.resize(n);
A = alot;
rep(i, 0, n - 1) (A[i] += MOD - s[i]) %= MOD;
B = Mul(B, exP0);
rep(i, 0, n - 1) B[i] = ((LL)B[i] * c % MOD + alot[i]) % MOD;
A = Mul(A, inverse(B)); A.resize(n);
rep(i, 0, n - 1) P0[i] = (P0[i] - A[i] + MOD) % MOD;
return P0;
}
int num[50], cntn;
void putint(int x) {
if(!x) return (void)puts("0");
cntn = 0;
while(x) num[++cntn] = x % 10, x /= 10;
dwn(i, cntn, 1) putchar(num[i] + ‘0‘); putchar(‘\\n‘);
return ;
}
vector <int> s, P;
int main() {
getinv(maxn - 1);
int n = read(), _n = 1, c = read();
while(_n <= n) _n <<= 1;
s.resize(n + 1);
rep(i, 1, n) s[i] = read();
if(!c) {
rep(i, 0, n) s[i] = (LL)s[i] * inv[2] % MOD;
s[0]++; if(s[0] >= MOD) s[0] -= MOD;
P = logarithm(s);
}
else s[0] = 1, P = solve(s, c);
rep(i, 1, n) putint(P[i]);
return 0;
}\\(^*\\)泰勒展开,在这里简单讲一下,其实很简单。
我们尝试用一个多项式函数去拟合一个其他函数,以 \\(f(x) = e^x\\) 为例。
设这个用来拟合的多项式函数的系数依次为 \\(a_0, a_1, a_2, \\cdots\\)
\\begin{equation}
e^x = \\sum_{i=0}^{+\\infty} {a_i x^i}
\\end{equation}
当 \\(x = 0\\) 时
\\[ 1 = a_0 \\]
将 \\((1)\\) 式两边分别求导,得到
\\begin{equation}
e^x = \\sum_{i=1}^{+\\infty} {a_i \\cdot i \\cdot x^i}
\\end{equation}
再让 \\(x = 0\\)
\\[ 1 = a_1 \\cdot 1! \\]
即
\\[ a_i = \\frac{1}{1!} \\]
注意上面为什么要打上阶乘符号,这是因为(我下边不想再写了)随着这个不断求导的过程,每次首项的 \\(a_i\\) 后面乘的数就会变成 \\(i!\\)。
于是得到
\\[ e^x = \\sum_{i=0}^{+\\infty} { \\frac{x^i}{i!} } \\]
这也就是我们 C 题一开始用到的式子,同理“在 \\(x - x_0\\) 处展开”就是把上面的 \\(x\\) 换元成 \\(x - x_0\\),然后每步对 \\(x\\) 的取值不再是 \\(0\\),变成了 \\(x_0\\)。