DFS

Posted 2020-10-19 wangguodong

这里总结了Leetcode中两道关于DFS的题

1. Combination Sum：https://leetcode.com/problems/combination-sum/#/description

按照例题的数据，假设给定的集合为{2,3,6,7}，目标值是7。直观来看，它的搜索空间是一棵树，如下图

 

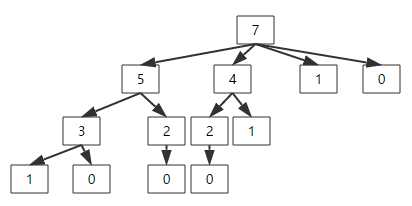
 树的每一层为减去集合中的元素后得到的结果，如，目标值分别减去2,3,6,7后，得到5,4,1,0，即为第一层的节点。当某一个节点的值为0时，表明从根节点到该节点的路径即为一个合法的结果。因此在编写程序时，应该保存路径，这里我使用了vector<int>& v。在编写DFS的递归代码时，应该将递归需要的变量全部以函数参数的形式传给函数，同时，递归调用往往在循环中发生，且一次递归调用仅表示一个层中的一个节点。代码如下：

void DFS(vector<vector<int>>& res, int idx, int sum, vector<int>& v,
    vector<int>& candidates, int target)
{
    if (sum == target) res.push_back(v);
    else if (sum<target)
    {
        for (int i = idx; i < candidates.size(); i++)
        {
            v.push_back(candidates[i]);
            DFS(res, i, candidates[i] + sum, v, candidates, target);
            // backtracking
            v.pop_back();
        }
    }
}

2. Generate Parentheses https://leetcode.com/problems/generate-parentheses/#/description

该题目的搜索空间如下：

 

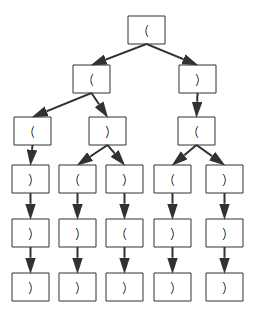
每次应该保留的参数为左右括号的个数和目前的括号序列，因为右括号的个数不能大于左括号的个数，所以循环递归时的循环条件为while (right<left)，此外，当左括号的个数等于了n，则应该不进入递归，所有进入递归的条件为if(left<n)。

代码如下：

void DFS(vector<string>& res, int n, int left, int right, string s)
{
    if (left == n&&left == right) { res.push_back(s); return; }
    if (left<n)
    {
        s += "(";
        left++;
        DFS(res, n, left, right, s);
        while (right<left)
        {
            s += ")";
            right++;
            DFS(res, n, left, right, s);
        }
    }
}