SLAM入门之视觉里程计：两视图对极约束 基础矩阵

Posted 2020-10-19 Brook@CV

在上篇相机模型中介绍了图像的成像过程，场景中的三维点通过“小孔”映射到二维的图像平面，可以使用下面公式描述：

\\[x = MX $$其中，$c$是图像中的像点，$M$是一个$3\\times4$的相机矩阵，$X$是场景中的三维点。 通过小孔相机模型，可知假如从像点$x$向相机的中心$C$反投影一条射线$\\overrightarrow{xC}$，则该射线必定经过对应像点的三维空间点$X$，但显然仅仅通过一个像点无法确定$X$的具体位置，因为在射线$\\overrightarrow{xC}$上的任意空间点都可以通过“小孔”映射为像点$x$。一个像点不行，那么如果两个相匹配的像点呢？ 设$x\'$是三维点$X$的另一个像点，其对应相机的中心为$C\'$，那么从像点也反投影一条射线$\\overrightarrow{x\'c\'}$，并且该射线也必定经过$X$，也就是说从一对相匹配的像点反投影两条射线，必定相交于空间三维点$X$，如下图  很显然，一对匹配的像点之间存在这某种约束关系，这种约束被称为**两视图的对极约束**。 本文主要介绍了两视图的对极约束-基础矩阵，并用几何和代数两种形式推导基础矩阵的表达形式以及从基础矩阵可以分解出相机的位姿（旋转和平移）。 ### 对极几何 对极几何描述的是两视图之间的内存射影关系，同一个三维点在两个不同的视角下的像点存在着约束关系，如下图三维点$X$在两幅图像的像点分分别为$x,x\'$  对极几何主要涉及以下几个元素： - 基线（Baseline），两个相机中心的连线$CC\'$称为基线 - 对极点 epipolar ，$e,e\'$是对极点，是基线和两个成像平面的交点，也就是两个相机在另一个成像平面的像点；$e$是右边的相机中心$C\'$在左边相机的像点，同样$e\'$是左边相机中心$C$在右边相机的像点。 - 对极平面 epipolar plane，任何过基线的平面都被才称为对极平面，两个相机的中心$C$和$C\'$，三维点$X$，以及其在两个相机的像点$x,x\'$，这5点必定在同一个对极平面上。当三维点$X$变化时，对极平面绕着基线旋转，形成对极平面束。 - 对极线 epipolar line ,对极平面和成像平面的交线，所有的对极线相交于极点。 从上面的几何元素可知，对极几何和相机的内参、外参没有关系，和场景的结构也没有关系，**仅和场景的一对匹配的像点有关系**。 ### 基础矩阵F 给定一对图像（同一场景不同视角得到的图像），从上面的图可知，对于第一幅图像上的任一像点$x$，在第二幅图像中都有一条与之对应的对极线$l\'$，该对极线是像点$x$与过第一个相机中心$C$射线在第二幅图像上的投影，并且第二幅图像中与$x$相匹配的像点$x\'$必定在该对极线上。因此，存在一个像点$x$到另一个图像上对极线$l\'$的映射： $$x \\rightarrow l\'\\]

基础矩阵\\(F\\)表示的就是这种从点到直线的映射。

F的几何推导

该推导来自《计算机视觉中的多视图几何》。

要将一幅图像上的像点\\(x\\)映射到另一幅图像对应的对极线\\(l\'\\)可以分为两步：第一步，将像点\\(x\\)映射到另一幅图像上与之对应的对极线\\(l\'\\)上的某点\\(x\'\\)上，\\(x\'\\)是\\(x\\)的匹配点；第二步，连接对极点\\(e\'\\)与点\\(x\'\\)得到的直线就是对极线\\(l\'\\)。

• 点通过平面转移 如下图，平面\\(\\pi\\)不通过两相机中心，过第一个相机的中心\\(C\\)和像点\\(x\\)的射线与\\(\\pi\\)相交于点\\(X\\)。该点\\(X\\)再投影到第二幅图像上得到像点\\(x\'\\),这个过程称为点通过平面的转移。
  
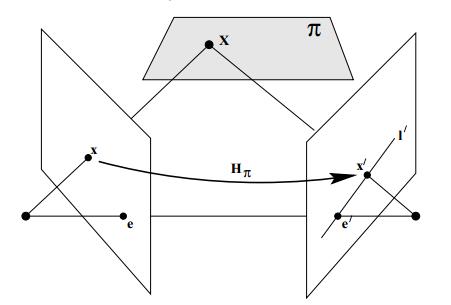
  点\\(X\\)位于像点\\(x\\)和相机中心确定的射线上，其在另一幅图像上的像点\\(x\'\\)必然位于该射线在另一幅图像的投影也就是对极线\\(l\'\\)上。点\\(x\\)和点\\(x\'\\)都是三维点\\(X\\)的像点，这样第一副图像上的像点集合\\(x_i\\)和第二幅图像上的像点集合\\(x\'_i\\)是射影等价的，它们都射影等价于共面的三维点集合\\(X_i\\)。因此，存在一个2D单应\\(H_{\\pi}\\)，把每一个点\\(x\\)映射到对应的点\\(x\'\\)上。

2D单应\\(H_{\\pi}\\)指的是将射影平面上的点集\\(x_i\\)映射到另一个射影平面的点集\\(x\'_i\\)上的射影变换，在实际情况中\\(x_i\\)和\\(x\'_i\\)通常是两幅图像上的像点，每幅图像都被视为一个射影平面。

• 构造对极线 给点点\\(x\'\\)，通过\\(x\'\\)和对极点\\(e\'\\)的对极线\\(l\'\\)可以表示为：$$l\'=e\'\\times x\'=[e\']{\\times}\\cdot x\'$$.
  又由于\\(x\'=H_{\\pi}x\\)（\\(H_{\\pi}\\)是将\\(x\\)变换为\\(x\'\\)的单应）,带入上式可得： $$l\'=[e\']{\\times}H_{\\pi} x$$
  定义$$F=[e\']{\\times}H{\\pi}$$
  这样就得到了从点\\(x\\)到对极线\\(l\'\\)的变换$$l\'=Fx$$
  以上就是基础矩阵\\(F\\)的推导过程。

• 基础矩阵\\(F\\)可以记为:\\(F=[e\']_{\\times}H_{\\pi}\\),其中\\(H_{\\pi}\\)是一幅图像上像点到另一幅图像上的2D单应，\\([e\']_{\\times}\\)是对极点\\(e\'\\)的反对称矩阵。由于\\([e\']_{\\times}\\)秩为2，\\(H_{\\pi}\\)的秩为3，基础矩阵\\(F\\)的秩为2.

• 对极约束
  由于\\(l\'=Fx\\)，而像点\\(x\'\\)在对极线\\(l\'\\)上，故可得到

\\[(x\')^Tl\'=(x\')^TFx=0 \\]

上式被称为对极约束，仅通过匹配的点对就可以求出两视图的基础矩阵\\(F\\)。

向量的叉积，反对称矩阵\\([e\']_{\\times}\\) 在射影几何中，一条直线有两点确定，如上面对极线有像点\\(x\'\\)和对极点\\(e\'\\)确定，并且可以表示为这两个点的叉积形式，有\\(l\'=e\'\\times x\'\\)。
设有两个向量\\(\\overrightarrow{a},\\overrightarrow{b}\\)，则这两个向量的叉积仍然是一个向量，并且垂直于\\(\\overrightarrow{a},\\overrightarrow{b}\\)所在的平面。其坐标表示如下：

\\[\\overrightarrow{a} \\times \\overrightarrow{b} = \\left[\\begin{array}{ccc}0&-z_1&y_1\\\\z_1&0&-x_1\\\\-y_1&x_1&0\\end{array}\\right] \\left[\\begin{array}{c}x_2\\\\y_2\\\\z_2\\end{array}\\right]=(\\overrightarrow{a}_{\\times})\\cdot \\overrightarrow{b} \\]

其中\\(\\overrightarrow{a}_{\\times}\\)称为向量\\(\\overrightarrow{a}\\)的反对称矩阵

\\[\\overrightarrow{a}_{\\times}=\\left[\\begin{array}{ccc}0&-z_1&y_1\\\\z_1&0&-x_1\\\\-y_1&x_1&0\\end{array}\\right] \\]

通过引入反对称矩阵，向量的叉积可以使用矩阵乘法的表示，形式非常简洁。

F的代数推导

该推导来自《视觉SLAM十四讲》

设以第一个相机作为坐标系三维空间的点\\(P=[X,Y,Z]\\)，其在两个相机的像点分别为\\(p_1,p_2\\)。由于第一个相机的中心作为世界坐标系的原点，也就是说第一个相机没有旋转和平移，通过小孔相机模型可得：

\\[p_1 = KP，p_2=K(RP+t) \\]

其中,\\(K\\)是相机的内参，\\(R,t\\)是第二个相机相对于第一个相机的旋转和平移。
从\\(p_1 = KP\\)可以得到\\(P=K^{-1}p_1\\)，带入第二个式子可得到：

\\[p_2=K(RK^{-1}p_1 + t) \\]

两边同时左乘\\(K^{-1}\\)，得到

\\[K^{-1}p_2=RK^{-1}p_1 + t \\]

设\\(x_1=K^{-1}p_1,x_2=K^{-1}p_2\\)，代入

\\[x_2=Rx_1+t \\]

两边同时左乘向量\\(t\\)的反对称矩阵\\(t_{\\times}\\),由于\\(t_{\\times}t=0\\)，消除\\(t\\)

\\[t_{\\times}x_2=t_{\\times}Rx_1 \\]

两边再同时左乘\\(x_2^T\\)

\\[x_2^Tt_{\\times}x_2=x_2^Tt_{\\times}Rx_1 \\]

由于\\(t_{\\times}x_2\\)是向量\\(t\\)和向量\\(x_2\\)的叉积，同时垂直于向量\\(t\\)和向量\\(x_2\\)，所以左边\\(x_2^Tt_{\\times}x_2=0\\)，得到

\\[x_2^Tt_{\\times}Rx_1=0 \\]

再将\\(x_1,x_2\\)换掉

\\[p_2^TK^{-T}t_{\\times}RK^{-1}p_1=0 \\]

上式是对极约束的另一种表示，该式子中仅包含像点，相机的旋转和平移，中间的矩阵就是基础矩阵\\(F\\)。

\\[p_2^TFp_1 = 0 , 其中 F=K^{-T}t_{\\times}RK^{-1} \\]

式子\\(F=K^{-T}t_{\\times}RK^{-1}\\)，可知假如相机的内参数\\(K\\)是已知的，提取中间的矩阵可到

\\[E = t_{\\times}R \\]

E被称为本质矩阵，其和基础矩阵相差相机的内参\\(K\\)。

通过匹配的点对计算相机的位姿

通过上面的知道，对于匹配的像点\\(p_1,p_2\\)以及基础矩阵\\(F\\)有如下关系：

\\[p_2^TFp_1 = 0 , 其中 F=K^{-T}t_{\\times}RK^{-1} \\]

也就是说，仅通过匹配的点对（最少7对）可以计算出两视图的基础矩阵\\(F\\)，然后再从\\(F\\)中分解得到相机的位姿势。

相机的相对位姿可以通过特征点匹配估计出来：

• 提取两幅图像的特征点，并进行匹配
• 利用匹配得像点计算两视图的基础矩阵\\(F\\)
• 从基础矩阵\\(F\\)中分解得到相机的选择矩阵\\(R\\)和平移向量\\(t\\)