杭电1023Train Problem II
Posted weeping
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了杭电1023Train Problem II相关的知识，希望对你有一定的参考价值。
地址：http://acm.hdu.edu.cn/showproblem.php?pid=1023
题目：
Train Problem II
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 7675 Accepted Submission(s): 4131
什么是Catalan数
说到Catalan数，就不得不提及Catalan序列，Catalan序列是一个整数序列，其通项公式是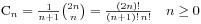
我们从中取出的
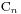就叫做第n个Catalan数，前几个Catalan数是：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, …咋看之下没什么特别的，但是Catalan数却是许多计数问题的最终形式。
Catalan数的一些性质
Catalan数的基本公式就是上个部分所列出的那样，但是却有一些变形和具体的性质：
1、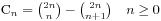
这是根据原来的式子推导出来的，大概过程是这样的：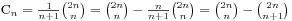
2、C(n)=C(n-1)*(4*n-2)/(n+1);
这个递推式很容易可以从原来的式子中获得
3、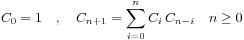
4、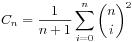
5、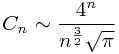
这个是Catalan数的增长趋势。
Catalan数在组合计算中的应用
1、矩阵链乘： P=a1×a2×a3×……×an，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？
思路：可以这样考虑，首先通过括号化，将P分成两个部分，然后分别对两个部分进行括号化。比如分成(a1)×(a2×a3.....×an)，然后再对(a1)和(a2×a3.....×an)分别括号化；又如分成(a1×a2)×(a3.....×an)，然后再对(a1×a2)和(a3.....×an)括号化。
设n个矩阵的括号化方案的种数为f(n)，那么问题的解为
f(n) = f(1)*f(n-1) + f(2)*f(n-2) + f(3)*f(n-3) + f(n-1)*f(1)。f(1)*f(n-1)表示分成(a1)×(a2×a3.....×an)两部分，然后分别括号化。
计算开始几项，f(1) = 1, f(2) = 1, f(3) = 2, f(4) = 5。结合递归式，不难发现f(n)等于h(n-1)。
2、一个栈(无穷大)的进栈序列为1，2，3，…，n，有多少个不同的出栈序列?
思路：这个与加括号的很相似，进栈操作相当于是左括号，而出栈操作相当于右括号。n个数的进栈次序和出栈次序构成了一个含2n个数字的序列。第0个数字肯定是进栈的数，这个数相应的出栈的数一定是第2i+1个数。因为如果是2i，那么中间包含了奇数个数，这奇数个肯定无法构成进栈出栈序列。
设问题的解为f(2n)， 那么f(2n) = f(0)*f(2n-2) + f(2)*f(2n-4) + f(2n-2)*f(0)。f(0) * f(2n-2)表示第0个数字进栈后立即出栈，此时这个数字的进栈与出栈间包含的数字个数为0，剩余为2n-2个数。f(2)*f(2n-4)表示第0个数字进栈与出栈间包含了2个数字，相当于1 2 2 1，剩余为2n-4个数字。依次类推。
假设f(0) = 1，计算一下开始几项，f(2) = 1, f(4) = 2, f(6) = 5。结合递归式，不难发现f(2n) 等于h(n)。
3、n个节点构成的二叉树，共有多少种情形？
思路：可以这样考虑，根肯定会占用一个结点，那么剩余的n-1个结点可以有如下的分配方式，T(0, n-1),T(1, n-2),...T(n-1, 0)，设T(i, j)表示根的左子树含i个结点，右子树含j个结点。
设问题的解为f(n)，那么f(n) = f(0)*f(n-1) + f(1)*f(n-2) + .......+ f(n-2)*f(1) + f(n-1)*f(0)。假设f(0) = 1，那么f(1) = 1, f(2) = 2, f(3) = 5。结合递推式，不难发现f(n)等于h(n)。
4、n对括号有多少种匹配方式？
思路：n对括号相当于有2n个符号，n个左括号、n个右括号，可以设问题的解为f(2n)。第0个符号肯定为左括号，与之匹配的右括号必须为第2i+1字符。因为如果是第2i个字符，那么第0个字符与第2i个字符间包含奇数个字符，而奇数个字符是无法构成匹配的。
通过简单分析，f(2n)可以转化如下的递推式 f(2n) = f(0)*f(2n-2) + f(2)*f(2n - 4) + ... + f(2n - 4)*f(2) + f(2n-2)*f(0)。简单解释一下，f(0) * f(2n-2)表示第0个字符与第1个字符匹配，同时剩余字符分成两个部分，一部分为0个字符，另一部分为2n-2个字符，然后对这两部分求解。 f(2)*f(2n-4)表示第0个字符与第3个字符匹配，同时剩余字符分成两个部分，一部分为2个字符，另一部分为2n-4个字符。依次类推。
假设f(0) = 1，计算一下开始几项，f(2) = 1, f(4) = 2, f(6) = 5。结合递归式，不难发现f(2n) 等于h(n)。
5、在圆上选择2n个点，将这些点成对连接起来使得所得到的n条线段不相交的方法数？
思路：以其中一个点为基点，编号为0，然后按顺时针方向将其他点依次编号。那么与编号为0相连点的编号一定是奇数，否则，这两个编号间含有奇数个点，势必会有个点被孤立，即在一条线段的两侧分别有一个孤立点，从而导致两线段相交。设选中的基点为A，与它连接的点为B，那么A和B将所有点分成两个部分，一部分位于A、B的左边，另一部分位于A、B的右边。然后分别对这两部分求解即可。
设问题的解f(n)，那么f(n) = f(0)*f(n-2) + f(2)*f(n-4) + f(4)*f(n-6) + ......f(n-4)*f(2) + f(n-2)*f(0)。f(0)*f(n-2)表示编号0的点与编号1的点相连，此时位于它们右边的点的个数为0，而位于它们左边的点为2n-2。依次类推。
f(0) = 1, f(2) = 1, f(4) = 2。结合递归式，不难发现f(2n) 等于h(n)。
6、求一个凸多边形区域划分成三角形区域的方法数？
思路：以凸多边形的一边为基，设这条边的2个顶点为A和B。从剩余顶点中选1个，可以将凸多边形分成三个部分，中间是一个三角形，左右两边分别是两个凸多边形，然后求解左右两个凸多边形。
设问题的解f(n)，其中n表示顶点数，那么f(n) = f(2)*f(n-1) + f(3)*f(n-2) + ......f(n-2)*f(3) + f(n-1)*f(2)。f(2)*f(n-1)表示三个相邻的顶点构成一个三角形，那么另外两个部分的顶点数分别为2和n-1。
设f(2) = 1，那么f(3) = 1, f(4) = 2, f(5) = 5。结合递推式，不难发现f(n) 等于h(n-2)。
7、描述：有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？
思路：可以将持5元买票视为进栈，那么持10元买票视为5元的出栈。这个问题就转化成了栈的出栈次序数。由应用三的分析直接得到结果，f(2n) 等于h(n)*n!*n!。
8、拥有 n+1 个叶子节点的二叉树的数量为h(n).例如 4个叶子节点的所有二叉树形态：
9、n*n的方格地图中，从一个角到另外一个角，不跨越对角线的路径数为h(n).例如， 4×4方格地图中的路径有：
10、圆桌周围有 2n个人，他们两两握手，但没有交叉的方案数为h(n)
11、说16个人按顺序去买烧饼，其中8个人每人身上只有一张5块钱，另外8个人每人身上只有一张10块钱。烧饼5块一个，开始时烧饼店老板身上没有钱。16个顾客互相不通气，每人只买一个。问这16个人共有多少种排列方法能避免找不开钱的情况出现。h(8)=1430，所以总数=1430*8！*8！
12、在图书馆一共6个人在排队，3个还《面试宝典》一书，3个在借《面试宝典》一书，图书馆此时没有了面试宝典了，求他们排队的总数？
h(3)=5；所以总数为5*3！*3！=180.
13、对于集合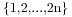
的不交叉划分的数目为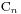，这里解释一下不交叉划分，我们对于集合{a,b}和{c,d}，假设他们组成了两个区间[a,b]和[c,d]，我们假设两个区间不重合，那么以下四种情况当做是不交叉的：a<c<d<b，a<b<c<d，c<a<b<d与c<d<a<b，就是说两个区间可以包含或者相离，那么此时我们称集合{a,b}和{c,d}是不交叉的。对于集合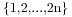，将里面元素两两分为一子集，共n个，若任意两个子集都是不交叉的，那么我们称此时的这个划分为一个不交叉划分。此时不交叉的划分数就是我们的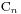了，证明也很容易，我们将每个子集中较小的数用左括号代替，较大的用右括号代替，那么带入原来的1至2n的序列中就形成了合法括号问题，就是我们第二点的结论。例如我们的集合{1,2,3,4,5,6}的不交叉划分有五个：{{1,2},{3,4},{5,6}}，{{1,2},{3,6},{4,5}}，{{1,4},{2,3},{5,6}}，{{1,6},{2,3},{4,5}}和{{1,6},{2,5},{3,4}}。
14、n层的阶梯切割为n个矩形的切法数也是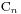。如下图所示：
这个证明是怎么进行的呢？我们先绘制如下的一张图片，即n为5的时候的阶梯：
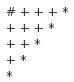
我们注意到每个切割出来的矩形都必需包括一块标示为*的小正方形，那么我们此时枚举每个*与#标示的两角作为矩形，剩下的两个小阶梯就是我们的两个更小的子问题了，于是我们的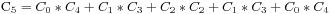
注意到这里的式子就是我们前面的性质3,因此这就是我们所求的结果了。
15、在一个2*n的格子中填入1到2n这些数值使得每个格子内的数值都比其右边和上边的所有数值都小的情况数也是。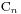
16、平面上连接可以形成凸包的2n个点分成2个一组连成n条线段，两两线段之间不相交的情况总数是，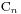
Catalan数问题的一个变形：
n+m个人排队买票，并且满足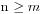
，票价为50元，其中n个人各手持一张50元钞票，m个人各手持一张100元钞票，除此之外大家身上没有任何其他的钱币，并且初始时候售票窗口没有钱，问有多少种排队的情况数能够让大家都买到票。
这个题目是Catalan数的变形，不考虑人与人的差异，如果m=n的话那么就是我们初始的Catalan数问题，也就是将手持50元的人看成是+1，手持100元的人看成是-1，任前k个数值的和都非负的序列数。
这个题目区别就在于n>m的情况，此时我们仍然可以用原先的证明方法考虑，假设我们要的情况数是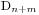
，无法让每个人都买到的情况数是
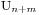，那么就有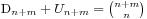
，此时我们求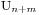，我们假设最早买不到票的人编号是k，他手持的是100元并且售票处没有钱，那么将前k个人的钱从50元变成100元，从100元变成50元，这时候就有n+1个人手持50元，m-1个手持100元的，所以就得到
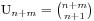，于是我们的结果就因此得到了，表达式是
。
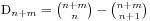关于Catalan数的变形还有很多，本身组合数学就是一门十分有趣的学科，通过不停地分析，求解我们能够不断增加自己思维的严谨性和全面性。
可以继续讲题目了：很明显这是卡特兰数，然而题目中n的取值最大为100，所以作为组合数的卡特兰数肯定非常大，int肯定不行，所以这题是卡特兰数+高精度；（这道题还挺良心，居然提示int存不下，让一直觉得hdoj好坑的我有点惊诧）；
用高精度模板就好了。
1 //大整数类的模板 2 #include <iomanip> 3 #include <iostream> 4 #include <algorithm> 5 #include <cstdio> 6 #include <cmath> 7 #include <cstring> 8 #include <queue> 9 #include <stack> 10 #include <map> 11 #include <vector> 12 13 #define MAXN 9999 14 #define MAXSIZE 10 15 #define DLEN 4 16 #define PI acos((double)-1) 17 #define E exp(double(1)) 18 19 using namespace std; 20 21 class BigNum 22 { 23 private: 24 int a[500]; //可以控制大数的位数 25 int len; //大数长度 26 public: 27 BigNum(){ len = 1;memset(a,0,sizeof(a)); } //构造函数 28 BigNum(const int); //将一个int类型的变量转化为大数 29 BigNum(const char*); //将一个字符串类型的变量转化为大数 30 BigNum(const BigNum &); //拷贝构造函数 31 BigNum &operator=(const BigNum &); //重载赋值运算符，大数之间进行赋值运算 32 33 friend istream& operator>>(istream&, BigNum&); //重载输入运算符 34 friend ostream& operator<<(ostream&, BigNum&); //重载输出运算符 35 36 BigNum operator+(const BigNum &) const; //重载加法运算符，两个大数之间的相加运算 37 BigNum operator-(const BigNum &) const; //重载减法运算符，两个大数之间的相减运算 38 BigNum operator*(const BigNum &) const; //重载乘法运算符，两个大数之间的相乘运算 39 BigNum operator/(const int &) const; //重载除法运算符，大数对一个整数进行相除运算 40 41 BigNum operator^(const int &) const; //大数的n次方运算 42 int operator%(const int &) const; //大数对一个int类型的变量进行取模运算 43 bool operator>(const BigNum & T)const; //大数和另一个大数的大小比较 44 bool operator>(const int & t)const; //大数和一个int类型的变量的大小比较 45 46 void print(); //输出大数 47 }; 48 BigNum::BigNum(const int b) //将一个int类型的变量转化为大数 49 { 50 int c,d = b; 51 len = 0; 52 memset(a,0,sizeof(a)); 53 while(d > MAXN) 54 { 55 c = d - (d / (MAXN + 1)) * (MAXN + 1); 56 d = d / (MAXN + 1); 57 a[len++] = c; 58 } 59 a[len++] = d; 60 } 61 BigNum::BigNum(const char*s) //将一个字符串类型的变量转化为大数 62 { 63 int t,k,index,l,i; 64 memset(a,0,sizeof(a)); 65 l=strlen(s); 66 len=l/DLEN; 67 if(l%DLEN) 68 len++; 69 index=0; 70 for(i=l-1;i>=0;i-=DLEN) 71 { 72 t=0; 73 k=i-DLEN+1; 74 if(k<0) 75 k=0; 76 for(int j=k;j<=i;j++) 77 t=t*10+s[j]-\'0\'; 78 a[index++]=t; 79 } 80 } 81 BigNum::BigNum(const BigNum & T) : len(T.len) //拷贝构造函数 82 { 83 int i; 84 memset(a,0,sizeof(a)); 85 for(i = 0 ; i < len ; i++) 86 a[i] = T.a[i]; 87 } 88 BigNum & BigNum::operator=(const BigNum & n) //重载赋值运算符，大数之间进行赋值运算 89 { 90 int i; 91 len = n.len; 92 memset(a,0,sizeof(a)); 93 for(i = 0 ; i < len ; i++) 94 a[i] = n.a[i]; 95 return *this; 96 } 97 istream& operator>>(istream & in, BigNum & b) //重载输入运算符 98 { 99 char ch[MAXSIZE*4]; 100 int i = -1; 101 in>>ch; 102 int l=strlen(ch); 103 int count=0,sum=0; 104 for(i=l-1;i>=0;) 105 { 106 sum = 0; 107 int t=1; 108 for(int j=0;j<4&&i>=0;j++,i--,t*=10) 109 { 110 sum+=(ch[i]-\'0\')*t; 111 } 112 b.a[count]=sum; 113 count++; 114 } 115 b.len =count++; 116 return in; 117 118 } 119 ostream& operator<<(ostream& out, BigNum& b) //重载输出运算符 120 { 121 int i; 122 cout << b.a[b.len - 1]; 123 for(i = b.len - 2 ; i >= 0 ; i--) 124 { 125 cout.width(DLEN); 126 cout.fill(\'0\'); 127 cout << b.a[i]; 128 } 129 return out; 130 } 131 132 BigNum BigNum::operator+(const BigNum & T) const //两个大数之间的相加运算 133 { 134 BigNum t(*this); 135 int i,big; //位数 136 big = T.len > len ? T.len : len; 137 for(i = 0 ; i < big ; i++) 138 { 139 t.a[i] +=T.a[i]; 140 if(t.a[i] > MAXN) 141 { 142 t.a[i + 1]++; 143 t.a[i] -=MAXN+1; 144 } 145 } 146 if(t.a[big] != 0) 147 t.len = big + 1; 148 else 149 t.len = big; 150 return t; 151 } 152 BigNum BigNum::operator-(const BigNum & T) const //两个大数之间的相减运算 153 { 154 int i,j,big; 155 bool flag; 156 BigNum t1,t2; 157 if(*this>T) 158 { 159 t1=*this; 160 t2=T; 161 flag=0; 162 } 163 else 164 { 165 t1=T; 166 t2=*this; 167 flag=1; 168 } 169 big=t1.len; 170 for(i = 0 ; i < big ; i++) 171 { 172 if(t1.a[i] < t2.a[i]) 173 { 174 j = i + 1; 175 while(t1.a[j] == 0) 176 j++; 177 t1.a[j--]--; 178 while(j > i) 179 t1.a[j--] += MAXN; 180 t1.a[i] += MAXN + 1 - t2.a[i]; 181 } 182 else 183 t1.a[i] -= t2.a[i]; 184 } 185 t1.len = big; 186 while(t1.a[len - 1] == 0 && t1.len > 1) 187 { 188 t1.len--; 189 big--; 190 } 191 if(flag) 192 t1.a[big-1]=0-t1.a[big-1]; 193 return t1; 194 } 195 196 BigNum BigNum::operator*(const BigNum & T) const //两个大数之间的相乘运算 197 { 198 BigNum ret; 199 int i,j,up; 200 int temp,temp1; 201 for(i = 0 ; i < len ; i++) 202 { 203 up = 0; 204 for(j = 0 ; j < T.len ; j++) 205 { 206 temp = a[i] * T.a[j] + ret.a[i + j] + up; 207 if(temp > MAXN) 208 { 209 temp1 = temp - temp / (MAXN + 1) * (MAXN + 1); 210 up = temp / (MAXN + 1); 211 ret.a[i + j] = temp1; 212 } 213 else 214 { 215 up = 0; 216 ret.a[i + j] = temp; 217 } 218 } 219 if(up != 0) 220 ret.a[i + j] = up; 221 } 222 ret.len = i + j; 223 while(ret.a[ret.len - 1] == 0 && ret.len > 1) 224 ret.len--; 225 return ret; 226 } 227 BigNum BigNum::operator/(const int & b) const //大数对一个整数进行相除运算 228 { 229 BigNum ret; 230 int i,down = 0; 231 for(i = len - 1 ; i >= 0 ; i--) 232 { 233 ret.a[i] = (a[i] + down * (MAXN + 1)) / b; 234 down = a[i] + down * (MAXN + 1) - ret.a[i] * b; 235 } 236 ret.len = len; 237 while(ret.a[ret.len - 1] == 0 && ret.len > 1) 238 ret.len--; 239 return ret; 240 } 241 int BigNum::operator %(const int & b) const //大数对一个int类型的变量进行取模运算 242 { 243 int i,d=0; 244 for (i = len-1; i>=0; i--) 245 { 246 d = ((d * (MAXN+1))% b + a[i])% b; 247 } 248 return d; 249 } 250 BigNum BigNum::operator^(const int & n) const //大数的n次方运算 251 { 252 BigNum t,ret(1); 253 int i; 254 if(n<0) 255 exit(-1); 256 if(n==0) 257 return 1; 258 if(n==1) HDU——1023 Train Problem IIC - Train Problem II——（HDU 1023 Catalan 数）
Train Problem II HDU 1023 卡特兰数