二叉搜索树

Posted 2020-10-19 ffxpy

有序字典是以有序集为基础的抽象数据类型。可用数组实现(二分法查询前驱后驱快速，但插入删除较麻烦)，链表实现(查询元素麻烦)。

因此用二叉搜索树实现字典。二叉搜索树就是一棵二叉树，保证左子树的元素小于根节点，右子树的元素大于根节点。
最坏情况下查找插入删除操作的复杂度都需要o（n），平均情况下的时间复杂度需要o（logn）

avl树

使最坏情况的复杂度降低到o（logn）的一种二叉搜索树。avl树保留二叉搜索树左子树右子树的关系，限制左子树与右子树的高度差不超过1，因为n个节点的近似满二叉树高度为logn，因此avl树的复杂度不超过o（logn）。

avl树的旋转变化

节点左子树的左子树过长

 

 

 

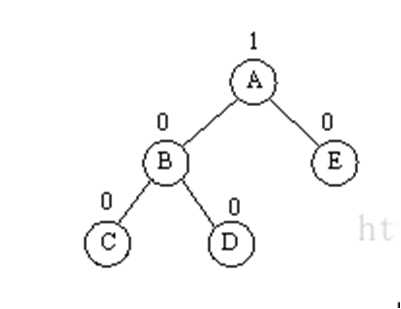
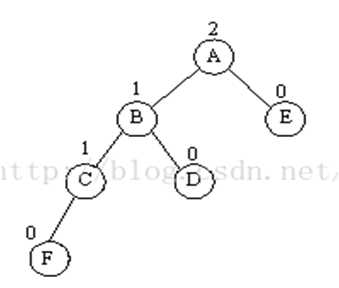
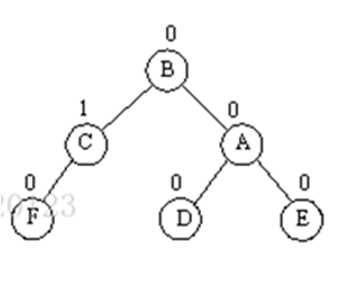
节点右子树的右子树过长同理

节点左子树的右子树过长

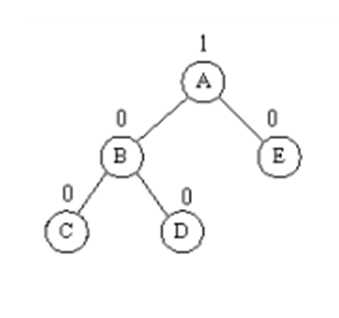
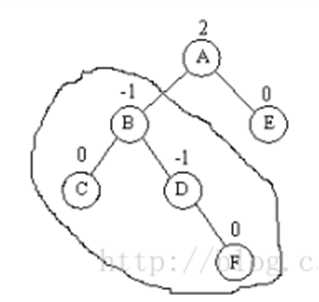
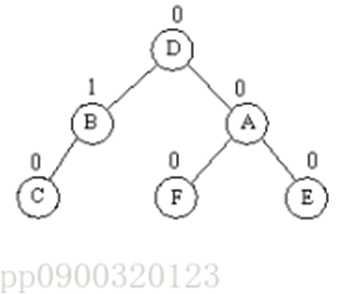
先对失衡节点a的左子树节点b进行左旋，使d成为原来b位置的根节点，此时失衡节点成为一个左子树的左子树过长节点，对a进行右旋，d成为根节点。

节点右子树的左子树过长同理

#include<iostream>
using namespace std;
int max(int a, int b) { return a > b ? a : b; }
typedef struct node* avlTree;
struct node {
    int val;
    int height;//储存的是每个节点的高度，而不是深度
    avlTree left;
    avlTree right;
};
int high(avlTree x) {
    return NULL == x ? 0 : x->height;
}

avlTree leftrotate(avlTree x1) {//节点左子树的左子树过长
    avlTree x2;
    x2 = x1->left;//位置关系
    x1->left = x2->right;
    x2->right = x1;
    x1->height = max(high(x1->left), high(x1->right)) + 1;
    x2->height = max(high(x2->left), high(x2->right)) + 1;//更新高度
    return x2;//返回新的根节点
}
avlTree rightrotate(avlTree x1) {//节点右子树的右子树过长
    avlTree x2;
    x2 = x1->right;//位置关系
    x1->right = x2->left;
    x2->left = x1;
    x1->height = max(high(x1->left), high(x1->right)) + 1;
    x2->height = max(high(x2->left), high(x2->right)) + 1;
    return x2;
}
avlTree leftrightrotate(avlTree x1) {//节点左子树的右子树过长
    x1->left = rightrotate(x1->left);//只是调用两次单旋的操作
    return leftrotate(x1);
}
avlTree rightleftrotate(avlTree x1) {//节点右子树的左子树过长
    x1->right = leftrotate(x1->right);
    return rightrotate(x1);
}

avlTree balance(avlTree x1) {
    if (high(x1->left) > high(x1->right)) {//左儿子的左儿子高度大于左儿子的右儿子高度，左旋，否则左右旋转
        if (high(x1->left->left) > high(x1->left->right))
            x1 = leftrotate(x1);
        else if (high(x1->left->left) < high(x1->left->right))
            x1 = leftrightrotate(x1);
    }
    else if (high(x1->left) < high(x1->right)) {//右儿子的右儿子高度大于右儿子的左儿子高度，右旋，否则右左旋转
        if (high(x1->right->right) > high(x1->right->left))
            x1 = rightrotate(x1);
        else if (high(x1->right->right) < high(x1->right->left))
            x1 = rightleftrotate(x1);
    }
    return x1;
}
avlTree insert(int v, avlTree x) {//建树插入
    if (NULL == x) {
        x = new node;
        x->height = 0;
        x->val = v;
        x->left = x->right = NULL;
    }
    else if (v < x->val) {
        x->left = insert(v, x->left);//递归查找，找到叶节点时就新建一个节点
        if (high(x->left) - high(x->right) == 2)
            x = balance(x);//建树时不断插入不断调整
    }
    else if (v > x->val) {
        x->right = insert(v, x->right);
        if (high(x->right) - high(x->left) == 2)
            x = balance(x);
    }
    x->height = max(high(x->left), high(x->right)) + 1;//更新高度
    return x;
}
int depth;
int find(int v, avlTree x) {//求节点的深度，也是利用递归，每次步数加一，找到输出深度
    depth++;
    if (NULL == x) return 0;
    if (v < x->val) {
        find(v, x->left);
    }
    else if (v > x->val) {
        find(v, x->right);
    }
    else {
        cout << depth;
        return 0;
    }
}
avlTree findmin(avlTree x) {//递归找树中最小值
    if (NULL == x) return NULL;
    else if (NULL == x->left) return x;
    else return findmin(x->left);
}
avlTree findmax(avlTree x) {//递归找树中最大值
    if (NULL == x) return NULL;
    else if (NULL == x->right) return x;
    else return findmax(x->right);
}

void Delete(int v, avlTree x) {//删除操作
    if (x == NULL) return;
    if (x->val > v)  Delete(v, x->left);
    else if (x->val < v) Delete(v, x->right);//查找被删除节点 
    else {
        if (x->left && x->right) {//一种情况是元素找到且左右子树不为空
            avlTree t;
            t = findmin(x->right);//找到该节点开始右子树的最小值（直接调用查找最小值函数）
            x->val = t->val;//删除节点用该被删除节点的右子树最小节点代替
            Delete(t->val, x->right);//删除用来代替删除节点的原来位置上的节点 递归
        }
        else {//另一种情况是左右子树有一边为空
            if (NULL == x->left)//直接把另一边提上来就好了
                x = x->right;
            else if (NULL == x->right)
                x = x->left;
            else {
                x = NULL;
            }
            return;
        }
    }
    x->height = max(high(x->left), high(x->right)) + 1;//回溯的时候判断平衡
    if (high(x->left) - high(x->right) == 2 || high(x->right) - high(x->left) == 2) {
        x = balance(x);
        x->height = max(high(x->left), high(x->right)) + 1;
    }
}
int a[100000];
int main() {
    int i, n;
    avlTree x = NULL;
    cin >> n;
    for (i = 1;i <= n;i++) {
        cin >> a[i];
        x = insert(a[i], x);
    }
    int m, flag;
    cin >> m;
    for (i = 1;i <= m;i++) {
        cin >> flag;
        depth = 0;
        if (flag == 1) {
            if (NULL == x) {
                cout << "-1" << endl;
                continue;
            }
            cout << findmax(x)->val << " ";
            find(findmax(x)->val, x);
            if (i != m) cout << endl;
            Delete(findmax(x)->val, x);
        }
        else if (flag == 2) {
            if (NULL == x) {
                cout << "-1";
                continue;
            }
            cout << findmin(x)->val << " ";
            find(findmin(x)->val, x);
            if (i != m) cout << endl;
            Delete(findmin(x)->val, x);
        }
        else if (flag == 3) {
            int g;
            cin >> g;
            x = insert(g, x);
        }
    }
    return 0;
}

 

未测试