平衡二叉树讲解
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了平衡二叉树讲解相关的知识,希望对你有一定的参考价值。
注:能用STL就尽量用STL
平衡二叉树(Balanced Binary Tree),又根据它的发明者命名为AVL树。
它或者是一颗空树,或者具有以下性质的二叉树:它的左子树和右子树的深度之差的绝对值不超过1,且它的左子树和右子树都是一颗平衡二叉树。
平衡因子(bf):结点的左子树的深度减去右子树的深度,那么显然-1<=bf<=1;
相关的算法有红黑树、AVL、Treap、伸展树(Splay)、SBT等。
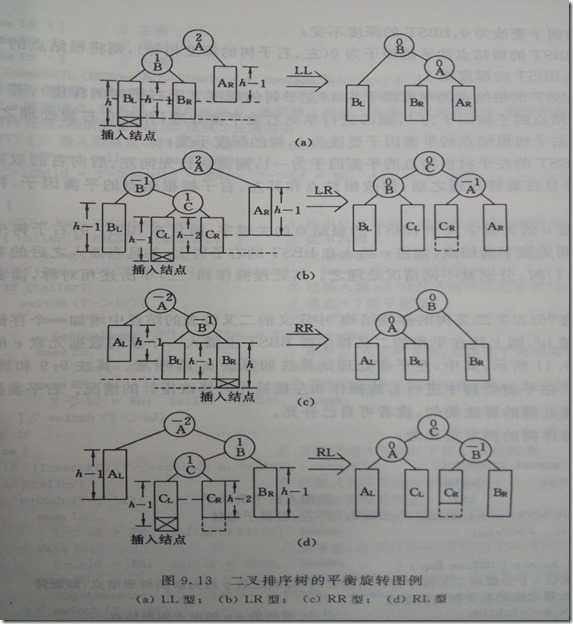
一、AVL算法
直接上图,清晰明了,分类讨论四种情况就行了。
二、伸展树(Splay)
(详细)http://blog.csdn.net/niuox/article/details/8018280
//kuangbin伸展树(Splay)模板 #define Key_value ch[ch[root][1]][0] const int MAXN = 500010; const int INF = 0x3f3f3f3f; int pre[MAXN],ch[MAXN][2],key[MAXN],size[MAXN]; int root,tot1; int sum[MAXN],rev[MAXN],same[MAXN]; int lx[MAXN],rx[MAXN],mx[MAXN]; int s[MAXN],tot2;//内存池和容量 int a[MAXN]; int n,q; //debug部分********************************** void Treavel(int x) { if(x) { Treavel(ch[x][0]); printf("结点:%2d: 左儿子 %2d 右儿子 %2d 父结点 %2d size = %2d\\n",x,ch[x][0],ch[x][1],pre[x],size[x]); Treavel(ch[x][1]); } } void debug() { printf("root:%d\\n",root); Treavel(root); } //以上是debug部分************************************** void NewNode(int &r,int father,int k) { if(tot2) r = s[tot2--];//取的时候是tot2--,存的时候就是++tot2 else r = ++tot1; pre[r] = father; ch[r][0] = ch[r][1] = 0; key[r] = k; sum[r] = k; rev[r] = same[r] = 0; lx[r] = rx[r] = mx[r] = k; size[r] = 1; } void Update_Rev(int r) { if(!r)return; swap(ch[r][0],ch[r][1]); swap(lx[r],rx[r]); rev[r] ^= 1; } void Update_Same(int r,int v) { if(!r)return; key[r] = v; sum[r] = v*size[r]; lx[r] = rx[r] = mx[r] = max(v,v*size[r]); same[r] = 1; } void push_up(int r) { int lson = ch[r][0], rson = ch[r][1]; size[r] = size[lson] + size[rson] + 1; sum[r] = sum[lson] + sum[rson] + key[r]; lx[r] = max(lx[lson],sum[lson] + key[r] + max(0,lx[rson])); rx[r] = max(rx[rson],sum[rson] + key[r] + max(0,rx[lson])); mx[r] = max(0,rx[lson]) + key[r] + max(0,lx[rson]); mx[r] = max(mx[r],max(mx[lson],mx[rson])); } void push_down(int r) { if(same[r]) { Update_Same(ch[r][0],key[r]); Update_Same(ch[r][1],key[r]); same[r] = 0; } if(rev[r]) { Update_Rev(ch[r][0]); Update_Rev(ch[r][1]); rev[r] = 0; } } void Build(int &x,int l,int r,int father) { if(l > r)return; int mid = (l+r)/2; NewNode(x,father,a[mid]); Build(ch[x][0],l,mid-1,x); Build(ch[x][1],mid+1,r,x); push_up(x); } void Init() { root = tot1 = tot2 = 0; ch[root][0] = ch[root][1] = size[root] = pre[root] = 0; same[root] = rev[root] = sum[root] = key[root] = 0; lx[root] = rx[root] = mx[root] = -INF; NewNode(root,0,-1); NewNode(ch[root][1],root,-1); for(int i = 0; i < n; i++) scanf("%d",&a[i]); Build(Key_value,0,n-1,ch[root][1]); push_up(ch[root][1]); push_up(root); } //旋转,0为左旋,1为右旋 void Rotate(int x,int kind) { int y = pre[x]; push_down(y); push_down(x); ch[y][!kind] = ch[x][kind]; pre[ch[x][kind]] = y; if(pre[y]) ch[pre[y]][ch[pre[y]][1]==y] = x; pre[x] = pre[y]; ch[x][kind] = y; pre[y] = x; push_up(y); } //Splay调整,将r结点调整到goal下面 void Splay(int r,int goal) { push_down(r); while(pre[r] != goal) { if(pre[pre[r]] == goal) { push_down(pre[r]); push_down(r); Rotate(r,ch[pre[r]][0] == r); } else { push_down(pre[pre[r]]); push_down(pre[r]); push_down(r); int y = pre[r]; int kind = ch[pre[y]][0]==y; if(ch[y][kind] == r) { Rotate(r,!kind); Rotate(r,kind); } else { Rotate(y,kind); Rotate(r,kind); } } } push_up(r); if(goal == 0) root = r; } int Get_kth(int r,int k) { push_down(r); int t = size[ch[r][0]] + 1; if(t == k)return r; if(t > k)return Get_kth(ch[r][0],k); else return Get_kth(ch[r][1],k-t); } //在第pos个数后面插入tot个数 void Insert(int pos,int tot) { for(int i = 0; i < tot; i++)scanf("%d",&a[i]); Splay(Get_kth(root,pos+1),0); Splay(Get_kth(root,pos+2),root); Build(Key_value,0,tot-1,ch[root][1]); push_up(ch[root][1]); push_up(root); } //删除子树 void erase(int r) { if(!r)return; s[++tot2] = r; erase(ch[r][0]); erase(ch[r][1]); } //从第pos个数开始连续删除tot个数 void Delete(int pos,int tot) { Splay(Get_kth(root,pos),0); Splay(Get_kth(root,pos+tot+1),root); erase(Key_value); pre[Key_value] = 0; Key_value = 0; push_up(ch[root][1]); push_up(root); } //将从第pos个数开始的连续的tot个数修改为c void Make_Same(int pos,int tot,int c) { Splay(Get_kth(root,pos),0); Splay(Get_kth(root,pos+tot+1),root); Update_Same(Key_value,c); push_up(ch[root][1]); push_up(root); } //将第pos个数开始的连续tot个数进行反转 void Reverse(int pos,int tot) { Splay(Get_kth(root,pos),0); Splay(Get_kth(root,pos+tot+1),root); Update_Rev(Key_value); push_up(ch[root][1]); push_up(root); } //得到第pos个数开始的tot个数的和 int Get_Sum(int pos,int tot) { Splay(Get_kth(root,pos),0); Splay(Get_kth(root,pos+tot+1),root); return sum[Key_value]; } //得到第pos个数开始的tot个数中最大的子段和 int Get_MaxSum(int pos,int tot) { Splay(Get_kth(root,pos),0); Splay(Get_kth(root,pos+tot+1),root); return mx[Key_value]; } void InOrder(int r) { if(!r)return; push_down(r); InOrder(ch[r][0]); printf("%d ",key[r]); InOrder(ch[r][1]); } int main() { while(scanf("%d%d",&n,&q) == 2) { Init(); char op[20]; int x,y,z; while(q--) { scanf("%s",op); if(strcmp(op,"INSERT") == 0) { scanf("%d%d",&x,&y); Insert(x,y); } else if(strcmp(op,"DELETE") == 0) { scanf("%d%d",&x,&y); Delete(x,y); } else if(strcmp(op,"MAKE-SAME") == 0) { scanf("%d%d%d",&x,&y,&z); Make_Same(x,y,z); } else if(strcmp(op,"REVERSE") == 0) { scanf("%d%d",&x,&y); Reverse(x,y); } else if(strcmp(op,"GET-SUM") == 0) { scanf("%d%d",&x,&y); printf("%d\\n",Get_Sum(x,y)); } else if(strcmp(op,"MAX-SUM") == 0) printf("%d\\n",Get_MaxSum(1,size[root]-2)); } } return 0; }
三、treap(树堆)
http://www.cnblogs.com/huangxincheng/archive/2012/07/30/2614484.html
以上是关于平衡二叉树讲解的主要内容,如果未能解决你的问题,请参考以下文章