Codeforces 903D Almost Difference

Posted 2020-10-19 xuzihanllaa

Codeforces 903D Almost Difference

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Let‘s denote a function

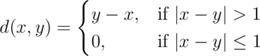
You are given an array a consisting of n integers. You have to calculate the sum of d(a_i,?a_j) over all pairs (i,?j) such that 1?≤?i?≤?j?≤?n.

Input

The first line contains one integer n (1?≤?n?≤?200000) — the number of elements in a.

The second line contains n integers a₁, a₂, ..., a_n (1?≤?a_i?≤?10⁹) — elements of the array.

Output

Print one integer — the sum of d(a_i,?a_j) over all pairs (i,?j) such that 1?≤?i?≤?j?≤?n.

Examples

Input

5
1 2 3 1 3

Output

4

Input

4
6 6 5 5

Output

0

Input

4
6 6 4 4

Output

-8

Note

In the first example:

1. d(a₁,?a₂)?=?0;
2. d(a₁,?a₃)?=?2;
3. d(a₁,?a₄)?=?0;
4. d(a₁,?a₅)?=?2;
5. d(a₂,?a₃)?=?0;
6. d(a₂,?a₄)?=?0;
7. d(a₂,?a₅)?=?0;
8. d(a₃,?a₄)?=??-?2;
9. d(a₃,?a₅)?=?0;
10. d(a₄,?a₅)?=?2.

 

分析：刚拿到这题，先想到的是：归并排序，仔细构思了一下感觉细节很多，不大好写；转而去想线段树（归并排序能解决的线段树都行），绝对值差在1及以内的直接不考虑就行了，那么对于一个值x，要考虑的区间范围是[1,x-2]U[x+2,+inf]，这样先离散化，然后线段树维护离散化后的下标，维护的信息有两个：区间和与区间计数（sum和cnt），因为对于x的查询结果sum和cnt，ans=cnt*x-sum，然后就是基本的单点更新，区间查询了。这道题要用高精度，我偷懒没写。主要原因是这道题其实用不着线段树，只要set或者map维护一下集合，然后维护前缀和即可。。这样写主程序代码长度不超过50行，比我100行的线段树代码清爽多了。

 

代码