归结反演法
- 鲁滨逊归结原理
检查子句集S中是否包含空子句。若包含,则S不可满足;若不包含,就在子句集中选择合适的子句进行归结,一旦通过归结能推出空子句,就说明子句集S是不可满足的。(这是我的理解:如果论据是真的,最后肯定会推出一个最终结论,如果是假的,最后的结论肯定就为空了也就是没有结论)
2. 一个十分重要的公式:
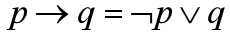
3. 子句的定义:
任何文字的析取(即并集、或)称为子句。
4. 把谓词公式化成子句集的步骤
1) 利用等价关系消去“→”和“↔”
例如公式
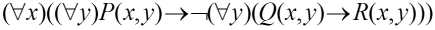
可等价变换为
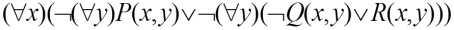
2) 利用等价关系把“¬”移到紧靠谓词的位置上上式经等价变换后
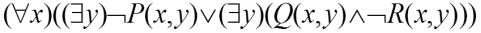
3)重新命名变元,使不同量词约束的变元有不同的名字
上式经变换后:
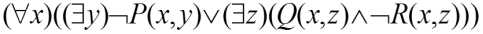
4)消去存在量词
a.存在量词不出现在全称量词的辖域内,则只要用一个新的个体常量替换受该量词约束的变元。(我的理解:说明两个量词没有关系)(比如说 存在某个x,那么用y=存在的某个x,即用y替换()即可)
b.存在量词位于一个或者多个全称量词的辖域内,此时要用函数替换受该存在量词约束的变元。(说明两个量词是有关系的,即函数关系)
上式中存在量词($y)及($z)都位于("x)的辖域内,所以需要用函数替换,设替换y和z的函数分别是f(x)和g(x),则替换后得到
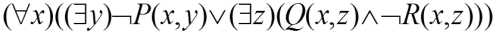
5)把全称量词全部移动到公式的左边
6)利用等价关系把公式化为标准形:(就是分配率)
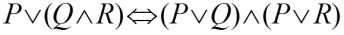
上式化为标准形后得到:
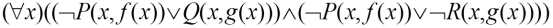
7)消去全称量词(我的理解是:就是直接去掉全称量词,既然所有的x都是了,那么自然可以省略)
8)对变元更名,使不同子句中的变元不同名
上式化为:
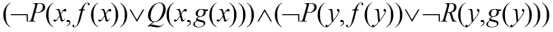
((x,y)只是变元,P、Q、R才是关系,自然可以用不同的方式命名)
9)消去合取词,就得到子句集
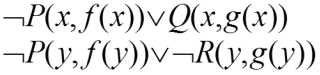
5. 命题逻辑中的归结原理
定义:若P是原子谓词公式,则称P与¬P为互补文字。在命题逻辑中,P为命题。
定义:设C1与C2是子句集中的任意两个子句。如果C1中的文字L1与C2中文字L2互补,那么从C1和C2中分别消去L1和L2,并将两个子句中余下的部分析取,构成一个新子句C12,则称这一过程为归结。称C12为C1和C2的归结式,C1和C2为C12的亲本子句。
定理:C12是其亲本子句C1与C2的逻辑结论。
定义定理的证明:
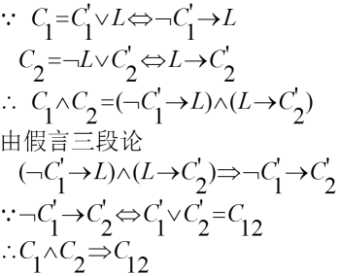
6. 归结反演法的具体步骤
以上都是基础知识,下面是归结反演的步骤。
1.否定Q,得到¬Q;
2.把¬Q并入到公式集F中,得到{F, ¬Q};
3.把公式集{F, ¬Q}化为子句集S;
4.应用归结原理对子句集S中的子句进行归结,并把每次归结得到的归结式都并入S中。如此反复进行,若出现了空子句,则停止归结,此时就证明了Q为真。
第一次写博客,理解得有什么不对的地方,或者有什么写得不好的地方请大家多多指教。。。