神经网络梯度弥散（消散）和梯度爆炸

Posted 2020-10-18 下路派出所

靠近输入的神经元会比靠近输出的神经元的梯度成指数级衰减

 

靠近输出层的hidden layer 梯度大，参数更新快，所以很快就会收敛；

而靠近输入层的hidden layer 梯度小，参数更新慢，几乎就和初始状态一样，随机分布。

这种现象就是梯度弥散（vanishing gradient problem）。

而在另一种情况中，前面layer的梯度通过训练变大，而后面layer的梯度指数级增大，这种现象又叫做梯度爆炸(exploding gradient problem)。

总的来说，就是在这个深度网络中，梯度相当不稳定(unstable)。

 

1.梯度消失（vanishing gradient problem）：

原因：例如三个隐层、单神经元网络：

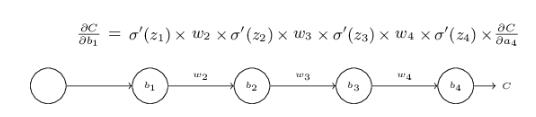
假设上面是一个三层hidden layer的神经网络，每一层只有一个neuron，我们下面的分析仅仅针对bias，w也是可以类比的。

C是损失函数。

每一层的输入为z，输出为a，其中有z = w*a + b。

上面的等式∂c/∂b1由每一层的导数乘上对应的w最后乘上∂c/∂a4组成。

我们给b1一个小的改变Δb1，它会在神经网络中起连锁反应，影响最后的C。

我们使用变化率∂c/∂b1～Δc/Δb1来估计梯度。接下来可以进行递推了。

 

先来计算Δb1对a1的影响。σ(z)为sigmoid函数。

 

 

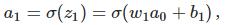
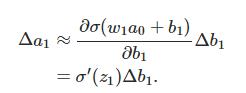
结果正好是上面∂c/∂b1等式的第一项，然后影响下一层的输出。

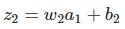
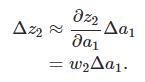
将上面推导出来的两个式子联合起来，就得到b1对于z2的影响：

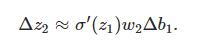
再和∂c/∂b1等式对比一下，惊喜！！

然后的推导就是完全一样了，每个neuron的导数，乘上w，最终得到C的变化量：

两边除以Δb1：

 

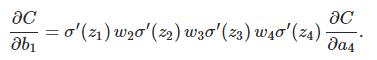
sigmoid导数图像：

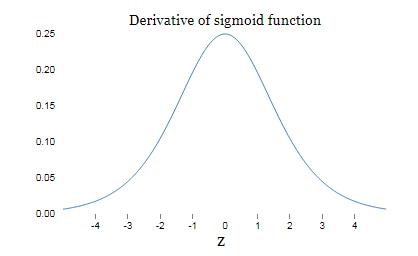
sigmoid导数在0取得最大值1/4。

如果我们使用均值为0，方差为1的高斯分布初始化参数w，有|w| < 1,所以有：

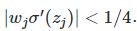
可以看出随着网络层数的加深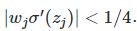的term也会变多，最后的乘积会指数级衰减，

这就是梯度弥散的根本原因。

而有人要问在train的时候如果参数w变得足够大，就可能使|w|>1,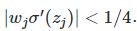就不满足了。

的确这样不会有梯度弥散问题，根据我们之前的分析，当|W|>1时，会使后面的layer参数指数级增加，从而引发梯度爆炸。

 

2.梯度爆炸（exploding gradient problem）：

当权值过大，前面层比后面层梯度变化更快，会引起梯度爆炸问题。

 

3.sigmoid时，消失和爆炸哪个更易发生？

量化分析梯度爆炸出现时a的树枝范围：因为sigmoid导数最大为1/4，故只有当abs(w)>4时才可能出现

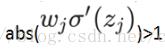
由此计算出a的数值变化范围很小，仅仅在此窄范围内会出现梯度爆炸问题。而最普遍发生的是梯度消失问题。

4.如何解决梯度消失和梯度爆炸？

梯度消失：

　　1.使用ReLU,maxout等替代sigmoid。

梯度爆炸：

　　1.使用Gradient Clipping(梯度裁剪)。通过Gradient Clipping，将梯度约束在一个范围内，这样不会使得梯度过大。 

 

Relu和sigmoid区别：

（1）sigmoid函数值在[0,1],ReLU函数值在[0,+无穷]，所以sigmoid函数可以描述概率，ReLU适合用来描述实数；

（2）sigmoid函数的梯度随着x的增大或减小和消失，而ReLU不会。