HDU1013，1163 ，2035九余数定理 快速幂取模

Posted 2020-10-18 Akmpfen

1、HDU1013求一个positive integer的digital root，即不停的求数位和，直到数位和为一位数即为数根。

一开始，以为integer嘛，指整型就行吧= =（too young），后来大数自然用字符串解决，然后get到一个新数论点九余数定理；

 

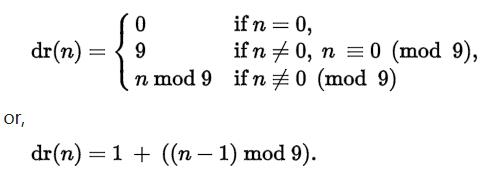
https://en.wikipedia.org/wiki/Digital_root

即：一个数的数根等于它模 9 的余数。（=》几个数之积的九余数=每个数的九余数之积的九余数。）

 

 2、HDU1163，2035求n^n的数根，即九余数定理加快速幂取模。

 快速幂：有递归，非递归，位运算实现等方式。主要思想就是x的m次方，可拆分为奇数时为x*（x^m）^2，偶数时为（x^m）^2；利用位运算就是利用n的二进制的位权值，如x^11即11的二进制表示为1011，x^11=x*2^0+x*2^1+x*2^3；由原来需要计算的11步，简化为了三步。HDU2035就是最基本的快速幂取模，取模是因为指数函数的增长速度太快，往往会超出long long的数据范围。

//HDU2035快速幂取模
#include <cstdio>
#include <iostream>

int pow(int x,int n)
{
    int base=x,ans=1;
    while(n)
    {
        if(n&1)    ans=(ans*base)%1000;
        base=(base*base)%1000;
        n>>=1;　　　　　　//位运算实现
    }
    return ans;
}
using namespace std;

int main()
{
    int a,b;
    while(cin >> a >> b,a||b)
    {
        cout << pow(a,b) << endl;
    }
    return 0;
}