支持向量分类方法

Posted 2020-10-18 夜空中最亮的星

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了支持向量分类方法相关的知识，希望对你有一定的参考价值。

1. 普通的支持向量积分类方法

import numpy as np


# 加载数据
def loadData():
    DataMatrix = []
    LabelMatrix = []
    with open("testSet.txt") as fr:
        for line in fr.readlines():
            datas = line.strip().split(\'\\t\')
            DataMatrix.append([float(datas[0]), float(datas[1])])
            LabelMatrix.append(float(datas[2]))
    return DataMatrix, LabelMatrix


# 选择两个不同的alpha的下标i,j
def selectJrand(i, m):
    j = i
    while j == i:
        j = int(np.random.uniform(0, m))
    return j


# 调整大于H 小于L的aj值
def clipAlpha(aj, H, L):
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj


def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
    dataMatrix = np.mat(dataMatIn)
    labelMat = np.mat(classLabels).transpose()
    b = 0
    m, n = np.shape(dataMatrix)
    alphas = np.mat(np.zeros((m, 1)))
    iter = 0
    while (iter < maxIter):
        alphaPairsChanged = 0
        for i in range(m):
            # wxi+b  w=i从1到N aiyixi累加再乘上xi
            fxi = float(np.multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[i, :].T)) + b
            # 预测值和真实值的差值
            Ei = fxi - float(labelMat[i])
            # alphas 在非边界上可以扩大或缩小
            if ((labelMat[i] * Ei < -toler) and (alphas[i] < C)) or ((labelMat[i] * Ei > toler) and (alphas[i] > 0)):
                j = selectJrand(i, m)
                fxj = float(np.multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[j, :].T)) + b
                Ej = fxj - float(labelMat[j])
                alphaIold = alphas[i].copy()
                alphaJold = alphas[j].copy()
                # 调整alpha[j]到 0，C之间
                if (labelMat[i] != labelMat[j]):
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if L == H:
                    print(\'H==L\')
                    continue
                # #=K11+k22-2K12
                eta = 2.0 * dataMatrix[i, :] * dataMatrix[j, :].T - dataMatrix[i, :] * dataMatrix[i, :].T - dataMatrix[
                                                                                                            j,
                                                                                                            :] * dataMatrix[
                                                                                                                 j, :].T
                if eta > 0:
                    print(\'eta>=0\')
                    continue
                alphas[j] -= labelMat[j] * (Ei - Ej) / eta
                # 对 alphasa[j]进行剪辑
                alphas[j] = clipAlpha(alphas[j], H, L)
                if (abs(alphas[j] - alphaJold) < 0.00001):
                    print("j not movving enough")
                    continue
                # a1,new=a1,old+y1y2(a2,old-a2,new)  把a2作为自变量
                alphas[i] += labelMat[j] * labelMat[i] * (alphaJold - alphas[j])
                # b1,new=bold-E1-y1K11(a1,new -a1,old)-y2K21(a2,new-a2,old)
                b1 = b - Ei - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[i, :].T - labelMat[
                                                                                                                  j] * (
                                                                                                                  alphas[
                                                                                                                      j] - alphaJold) * dataMatrix[
                                                                                                                                        i,
                                                                                                                                        :] * dataMatrix[
                                                                                                                                             j,
                                                                                                                                             :].T
                # b2,new=bold-E2-y1K12(a1,new-a1,old)-y2K22(a2,new-a2,old)
                b2 = b - Ej - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[j, :].T - labelMat[
                                                                                                                  j] * (
                                                                                                                  alphas[
                                                                                                                      j] - alphaJold) * dataMatrix[
                                                                                                                                        j,
                                                                                                                                        :] * dataMatrix[
                                                                                                                                             j,
                                                                                                                                             :].T
                if (0 < alphas[i]) and (C > alphas[i]):
                    b = b1
                elif (0 < alphas[j]) and (C > alphas[j]):
                    b = b2
                else:
                    b = (b1 + b2) / 2.0
                alphaPairsChanged += 1
                print(\'iter:%d i:%d,pairs change %d\' % (iter, i, alphaPairsChanged))
        if (alphaPairsChanged == 0):
            iter += 1
        else:
            iter = 0
        print(\'iteration number:%d\' % iter)
    return b, alphas


# 画图
def plotThePicture(VectDoc, alphas, b):
    import matplotlib.pyplot as plt
    DataMatrix, LabelMatrix = loadData()
    dataArra = np.array(DataMatrix)
    n = np.shape(dataArra)[0]
    xcord1 = []
    ycord1 = []
    xcord2 = []
    ycord2 = []
    xcord3 = []
    ycord3 = []
    for i in range(n):
        if i not in VectDoc:
            if int(LabelMatrix[i]) == 1.0:
                xcord1.append(dataArra[i][0])
                ycord1.append(dataArra[i][1])
            else:
                xcord2.append(dataArra[i][0])
                ycord2.append(dataArra[i][1])
        else:
            xcord3.append(dataArra[i][0])
            ycord3.append(dataArra[i][1])
    w = np.array(calcWs(alphas, dataArra, LabelMatrix))
    x = np.arange(-2.0, 10.0, 0.1)
    # fxi = float(np.multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[i, :].T)) + b
    # for j in range(len(x)):
    s = b[0][0]
    t1 = w[0][0]
    t2 = w[1][0]
    y = np.array((-s - t1 * x) / t2)[0]
    # xnew = np.mat(np.array([x[j], x[j]]))
    # yu = (xnew * w) + b
    # y.append(np.array(yu)[0][0])
    # y = (x * w) + b
    # 画出支持向量所在的直线
    y1 = np.array((1 - s - t1 * x) / t2)[0]
    y2=np.array((-1-s-t1*x)/t2)[0]

    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c="red", marker=\'s\')
    ax.scatter(xcord2, ycord2, s=30, c=\'green\')
    ax.scatter(xcord3, ycord3, s=30, c="blue", marker=\'*\')
    ax.plot(x, y)
    ax.plot(x,y1)
    ax.plot(x,y2)
    plt.xlabel(\'x1\')
    plt.ylabel(\'y1\')
    plt.show()


def calcWs(alphas, dataArr, classLabels):
    x = np.mat(dataArr)
    labelMat = np.mat(classLabels).transpose()
    m, n = np.shape(x)
    w = np.zeros((n, 1))
    for i in range(m):
        if alphas[i] > 0.0:
            w += np.multiply(alphas[i] * labelMat[i], x[i, :].T)
    return w


dataMatrix, LabelMatrix = loadData()
b, alphas = smoSimple(dataMatrix, LabelMatrix, 0.6, 0.001, 40)
print(b)
print(\'-\' * 20)
# print(alphas[alphas !=0])
VectorDoc = []
for i in range(100):
    if alphas[i] > 0.0:
        print(dataMatrix[i], LabelMatrix[i],alphas[i])
        VectorDoc.append(i)

plotThePicture(VectorDoc, alphas, b)

2.完整的SMO分类

最小最优化(SMO)算法,就是要求解凸二次规划的对偶问题

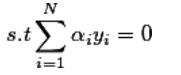
$formdata=\min_{\alpha}+\frac1{\2}\sum_{i=1}^{N}\sum_{j=1}^{N}+\alpha_{i}\alpha_{j}y_{i}y_{j}K(x_i,x_j)-\sum_{i=1}^{N}\alpha_{i}$

$formdata=0<=\alpha_{i}<=C$ ，i =1,2,...,N

在这个问题中变量是拉格朗日乘子，一个变量 $formdata=\alpha_{i}$ 对应于一个样本点 $formdata=(x_{i},y_{i})$ ,变量的总数等于训练样本容量N

SMO 算法是一种启发式算法，如果所有变量的解都满足此最优化问题的KKT条件，那么这个最优化问题的解得到了，因为KKT条件是该问题最优化问题的充分必要条件，否则，选择两个变量，固定其他变量，针对这两个变量构建一个二次规划问题，则这个二次规划问题关于两个变量的解应该更接近原始二次规划问题的解，因为这会使得原始二次规划问题的目标函数值变的更小,子问题中有两个变量，一个是违反KKT条件最严重的哪一个，另一个是|Ei-Ej|约束条件最大的哪一个

其实子问题中只有一个自由变量假设 $formdata=\alpha_1,\alpha_2$ 为两个变量, $formdata=\alpha_3,\alpha_4,....,\alpha_N$ 固定，那么由约束条件可知

$formdata=\alpha_1=-y_{1}\sum_{i=1}^{N}\alpha_{i}y_{i}$

如果其中一个确定，那么另一个也确定

解题方法

假设选两个变量 $formdata=\alpha_1,\alpha_2$ ，其他变量固定 $formdata=\alpha_i(i=3,4,...,N)$ 于是最优化问题的子问题可以写成

$formdata=min_{\alpha_{1},\alpha_{2}}+W(\alpha_1,\alpha_2)=\frac1{2}K_{11}\alpha_{{1}^2+\frac1{2}K_{22}\alpha_{2}^2+y_{1}y_{2}K_{12}\alpha_{1}\alpha_{2}-(\alpha_{1}+\alpha_{2}) +y_{1}\alpha_1+\sum_{i=3}^{N}y_{i}\alpha_{i}K_{i1}+y_{2}\alpha_{2}+\sum_{i=3}^{N}y_{i}\alpha_{i}K_{i2}$

$formdata=s.t+\alpha_{1}y_{1}+\alpha_{2}y_{2}=-\sum_{i=3}^{N}y_{i}\alpha{i}=\varepsilon$

$formdata=0<=\alpha_{i}<=C$ ，i =1,2,...,N

其中, $formdata=K_{ij}=K(x_{i},x_{j}),i,j=1,2,...,N,+\varepsilon$ 是常数，目标函数省略了不含 $formdata=\alpha_1,\alpha_2$ 的常数项

记初始解为 $formdata=\alpha_{1}^{old},\alpha_{2}^{old}$ , 最优解为 $formdata=\alpha_{1}^{new},\alpha_{2}^{new}$ 那么 y1和y2只能取 1或-1

则如果 y1!=y2 $formdata=L=max(0,\alpha_{2}^{old}-\alpha_{1}^{old}),+H=min(C,C+\alpha_{2}^{old}-\alpha_{1}^{old})$

如果 y1==y2 $formdata=L=max(0,\alpha_{2}^{old}+\alpha_{1}^{old}-C),+H=min(C,\alpha_{2}^{old}+\alpha_{1}^{old})$

下面首先求沿着约束方向未经剪辑即为考虑约束条件 $formdata=0<=\alpha_{i}<=C$ 时 $formdata=\alpha_{2}$ 的最优解 $formdata=\alpha_{2}^{new,unc}$ ，然后在剪辑求 $formdata=\alpha_{2}^{new}$

$formdata=g(x)=\sum_{i=1}^{N}\alpha_{i}\y_{i}K(x_{i},x)+b$

$formdata=E_{i}=g(x_{i})-y_{i}=[\sum_{i=1}^{N}\alpha_{i}\y_{i}K(x_{i},x)+b]-y_{i}$

当 i=1,2时 $formdata=E_{i}$ 为函数g(x)对输入xi的预测值与真实值yi之差

定理最优化问题沿着约束方向未经剪辑的解为

$formdata=\alpha_{2}^{new,unc}=\alpha_{2}^{old}+\frac{y_{2}(E_{1}-E_{2})}{\eta}$

其中 $formdata=\eta=K_{11}+K_{22}-2K_{12}$

$formdata=\alpha_{2}^{new}$ 剪辑其实就是限定范围在 L到H 大于H就赋值为H，小于L就赋值为L,其余不变

$formdata=\alpha_{1}^{new}=\alpha_{1}^{old}+y_{1}y_{2}(\alpha_{2}^{old}-\alpha_{2}^{new})$

证明如下:

# 完整版SMO算法
import numpy as np


class optStruct:
    # dataMatrix 数据数据矩阵
    # classLabels 类别标签
    # C 惩罚参数
    # toler表示错误率
    # alphas表示前置系数
    # b 表示常数项
    # eCache缓存误差 第一列表示eCache是否有效，第二列给出的是实际的E值
    def __init__(self, dataMatrix, classLabels, C, toler):
        self.x = dataMatrix
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = np.shape(dataMatrix)[0]
        self.alphas = np.mat(np.zeros((self.m, 1)))
        self.b = 0
        self.eCache = np.mat(np.zeros((self.m, 2)))

    # 随机选择一个j
    def selectJrand(self, i, m):
        j = i
        while j != i:
            j = int(np.random.uniform(0, m))
        return j

    #  计算预测值与真实值的误差
    def calcEk(self, k):
        fxk = float(np.multiply(self.alphas, self.labelMat).T * (self.x * self.x[k, :].T)) + self.b
        Ek = fxk - float(self.labelMat[k])
        return Ek

    # 内循环选择一个j 选择条件 |Ei-Ej|的值最大
    def selectJ(self, i, Ei):
        maxK = -1;
        maxDeltaE = 0;
        Ej = 0
        self.eCache[i] = [1, Ei]
        # 返回有效元素所在的index序列号
        validEcacheList = np.nonzero(self.eCache[:, 0].A)[0]
        if (len(validEcacheList)) > 1:
            for k in validEcacheList:
                if k == i: continue
                Ek = self.calcEk(k)
                deltaE = np.abs(Ei - Ek)
                if (deltaE > maxDeltaE):
                    maxK = k
                    maxDeltaE = deltaE
                    Ej = Ek
            return maxK, Ej
        else:  # 如果是第一次循环  随机选择一个j
            j = self.selectJrand(i, self.m)
            Ej = self.calcEk(j)
            return j, Ej

    # 把先相应数据存入缓存
    def updateEk(self, k):
        Ek = self.calcEk(k)
        self.eCache[k] = [1, Ek]

    def innerL(self, i):
        Ei = self.calcEk(i)
        # yi(w*xi+b)>=1-u
        # 违反KKT条件 的一个alphas
        # 列出所有的KKT条件   1.  ai=0---->yig(xi)>=1
        #                     2.0<ai<C-->yig(xi)=1
        #                     3. ai=C-->yig(xi)<=1
        # 一般首先遍历所有满足 2. 条件的样本点，即在间隔边界上的支持向量，检验他们是否满足KKT条件，如果读满足，则遍历整个训练集看是否满足KKT条件
        if ((self.labelMat[i] * Ei < -self.tol) and (self.alphas[i] < self.C)) or (
                    (self.labelMat[i] * Ei > self.tol) and (self.alphas[i] > 0)):
            j, Ej = self.selectJ(i, Ei)
            alphaIold = self.alphas[i].copy()
            alphaJold = self.alphas[j].copy()
            if (self.labelMat[i] != self.labelMat[j]):
                L = max(0, self.alphas[j] - self.alphas[i])
                H = min(self.C, self.C + self.alphas[j] - self.alphas[i])
            else:
                L = max(0, self.alphas[j] + self.alphas[i] - self.C)
                H = min(self.C, self.alphas[j] + self.alphas[i])
            if L == H: print(\'H==L\'); return 0
            eta = 2.0 * self.x[i, :] * self.x[j, :].T - self.x[i, :] * self.x[i, :].T - self.x[j, :] * self.x[j, :].T
            if eta >= 0: print(\'eta>=0\');return 0
            self.alphas[j] -= self.labelMat[j] * (Ei - Ej) / eta
            self.alphas[j] = self.clipAlpha(self.alphas[j], H, L)
            self.updateEk(j)
            if (np.abs(self.alphas[j] - alphaJold) < 0.00001):
                print(\'j not moving enough\')
                return 0
            # 更新alphas i
            self.alphas[i] += self.labelMat[i] * self.labelMat[j] * (alphaJold - self.alphas[j])
            self.updateEk(i)
            b1 = self.b - Ei - self.labelMat[i] * (self.alphas[i] - alphaIold) * self.x[i, :] * self.x[i, :].T - \\
                 self.labelMat[j] * (self.alphas[j] - alphaJold) * self.x[i, :] * self.x[j, :].T
            b2 = self.b - Ej - self.labelMat[i] * (self.alphas[i] - alphaIold) * self.x[i, :] * self.x[j, :].T - \\
                 self.labelMat[j] * (self.alphas[j] - alphaJold) * self.x[j, :] * self.x[j, :].T
            if (self.alphas[i] > 0) and (self.alphas[i] < self.C):
                self.b = b1
            elif (self.alphas[j] > 0) and (self.alphas[j] < self.C):
                self.b = b2
            else:
                self.b = (b1 + b2) / 2.0
            return 1
        else:
            return 0

    # 修剪
    def clipAlpha(self, aj, H, L):
        if aj > H:
            aj = H
        if L > aj:
            aj = L
        return aj


def smop(dataMatin, classLabels, C, toler, maxIter, kTup=(\'lin\', 0)):
    os = optStruct(np.mat(dataMatin), np.mat(classLabels).transpose(), C, toler)
    iter = 0
    entireSet = True
    alphaPairsChanged = 0
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
        alphaPairsChanged = 0
        # 遍历所有的值
        if entireSet:
            for i in range(os.m):
                alphaPairsChanged += os.innerL(i)
            print(\'fullSet,iter:%d i:%d ,pairs changed %d\' % (iter, i, alphaPairsChanged))
            iter += 1
        else:
            # 遍历非边界值
            nonBoundIs = np.nonzero((os.alphas.A > 0) * (os.alphas.A < os.C))[0]
            for i in nonBoundIs:
                alphaPairsChanged += os.innerL(i)
                print(\'non-bound,iter:%d i:%d,pairs changed %d\' % (iter, i, alphaPairsChanged))
            iter += 1
        if entireSet:
            entireSet = False
        elif alphaPairsChanged == 0:
            entireSet = True
    print(\'iteration number:%d\' % iter)
    return os.b, os.alphas


def loadData():
    DataMatrix = []
    LabelMatrix = []
    with open("testSet.txt") as fr:
        for line in fr.readlines():
            datas = line.strip().split(\'\\t\')
            DataMatrix.append([float(datas[0]), float(datas[1])])
            LabelMatrix.append(float(datas[2]))
    return DataMatrix, LabelMatrix


def calcWs(alphas, dataArr, classLabels):
    x = np.mat(dataArr)
    labelMat = np.mat(classLabels).transpose()
    m, n = np.shape(x)
    w = np.zeros((n, 1))
    for i in range(m):
        if alphas[i] > 0.0:
            w += np.multiply(alphas[i] * labelMat[i], x[i, :].T)
    return w


def plotThePicture(VectDoc, alphas, b):
    import matplotlib.pyplot as plt
    DataMatrix, LabelMatrix = loadData()
    dataArra = np.array(DataMatrix)
    n = np.shape(dataArra)[0]
    xcord1 = []
    ycord1 = []
    xcord2 = []
    ycord2 = []
    xcord3 = []
    ycord3 = []
    for i in range(n):
        if i not in VectDoc:
            if int(LabelMatrix[i]) == 1.0:
                xcord1.append(dataArra[i][0])
                ycord1.append(dataArra[i][1])
            else:
                xcord2.append(dataArra[i][0])
                ycord2.append(dataArra[i][1])
        else:
            xcord3.append(dataArra[i][0])
            ycord3.append(dataArra[i][1])
    w = np.array(calcWs(alphas, dataArra, LabelMatrix))
    x = np.arange(-2.0, 10.0, 0.1)
    # fxi = float(np.multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[i, :].T)) + b
    # for j in range(len(x)):
    s = b[0][0]
    t1 = w[0][0]
    t2 = w[1][0]
    y = np.array((-s - t1 * x) / t2)[0]
    # xnew = np.mat(np.array([x[j], x[j]]))
    # yu = (xnew * w) + b
    # y.append(np.array(yu)[0][0])
    # y = (x * w) + b
    # 画出支持向量所在的直线
    y1 = np.array((1 - s - t1 * x) / t2)[0]
    y2 = np.array((-1 - s - t1 * x) / t2)[0]

    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c="red", marker=\'s\')
    ax.scatter(xcord2, ycord2, s=30, c=\'green\')
    ax.scatter(xcord3, ycord3, s=30, c="blue", marker=\'*\')
    ax.plot(x, y)
    ax.plot(x, y1)
    ax.plot(x, y2)
    plt.xlabel(\'x1\')
    plt.ylabel(\'y1\')
    plt.show()


dataArra, LabelArra = loadData()
b, alphas = smop(dataArra, LabelArra, 0.6, 0.001, 100)
print(b)
print(\'-\' * 20)
print(alphas[alphas > 0])

VectorDoc = []
for i in range(100):
    if alphas[i] > 0.0:
        print(dataArra[i], LabelArra[i], alphas[i])
        VectorDoc.append(i)

plotThePicture(VectorDoc, alphas, b)
np.nonzero()

以上是关于支持向量分类方法的主要内容，如果未能解决你的问题，请参考以下文章

机器学习基础从感知机到支持向量机&支持向量机的多分类方法

支持向量机分类方法的优缺点