以BZOJ 2002 弹飞绵羊为例学习有根树LCT(Link-Cut Tree)
注:本文非常简单,只涉及有根树LCT,对于无根树,LCT还有几个本文没有提到的操作,以后慢慢更新 =v=
知识储备
- [x] splay
- [x] 树链剖分
题意
有一棵\\(n\\)个节点的有根树,动态修改父子关系(保证仍是一棵有根树),并询问某节点深度。
题解
这是一道LCT(Link-Cut Tree)的模板题。
Link-Cut Tree (又)是Tarjan发明的一种算法,可以解决一类动态树问题。“动态树问题”就是像本题这种,随时修改树的结构的问题。
LCT在思想上有些类似于树链剖分。
回顾一下树剖:
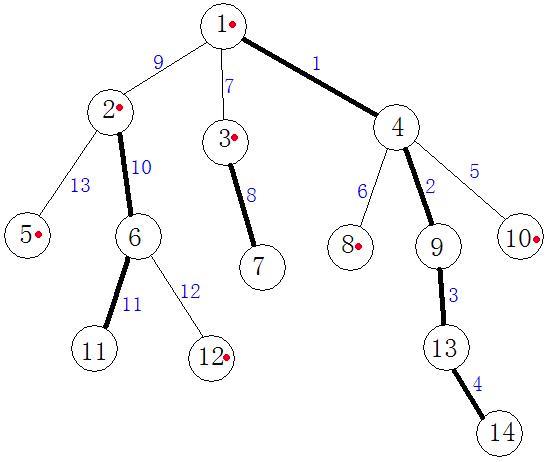
在树剖中,我们把边分为重边和轻边两种,重边相连形成了重链,而重链可以用线段树维护。
美中不足的是,线段树无法完成“动态修改”的需要。那么什么数据结构最灵活,能随时断开/连接呢?那当然是——splay啦。
所以,LCT就是用好多棵splay平衡树来维护原树上的每条“实链”(类似树剖的“重链”)。
具体是如何维护的呢?可以看这幅图:
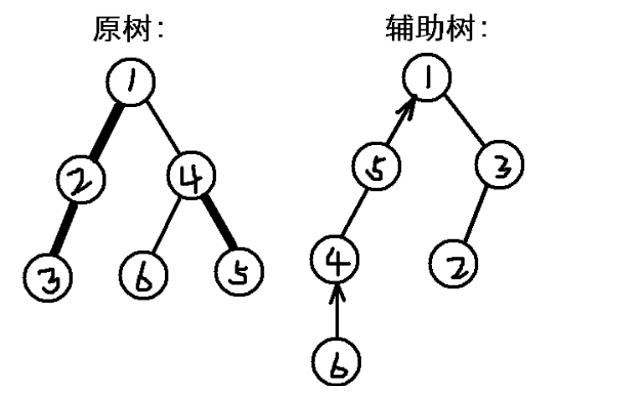
左图是原树,右图是我们建出的splay树。
左图中的每一条实链都对应着右图中一棵“完整的”(不带“箭头”的)平衡树,如(1,2,3)、(4,5)、(6)各自组成一棵平衡树。每棵完整的平衡树都把节点在原树中的深度作为关键字,例如4比5深度小,所以是5的左儿子;3比1深度大,所以是1的右儿子。当然,身为splay,右图不是左图对应的唯一平衡树,还有很多种可能的合法平衡树。
而左图上的每一条虚边(u, v),则使用了一种“单向边”来维护:设u是父亲、v是儿子,则在右图中,v所在的平衡树的根节点“认”u所在的平衡树的根节点为父亲,而反过来,父亲却不认儿子。这种关系在右图中用单向的箭头表示了。例如,在原图中,(1, 4)是一条虚边,4所在的平衡树的根节点是5,1所在的平衡树的根节点是1,所以右图中fa[5] = 1,而1却不认为5是它的儿子。
好的,现在你对LCT如何实现有了个初步的印象了!那么接下来,我们逐个学习LCT涉及到的操作。
操作1:Access
Access操作是所有LCT操作的基础!Access(u)会把根节点到u路径上的所有边都变成“实边”,使得u和根节点处于一棵完整平衡树中。
代码实现:
void access(int u){
int v = 0; //一开始v是空节点,其余时刻v都是要与u连接的小平衡树的根节点
while(u){
splay(u); //将u在旋至它所在的平衡树的根节点
rs[u] = v; //因为v深度更大,所以让v作为u的右儿子
upt(u); //修改儿子后,莫忘调用单节点更新函数
v = u, u = fa[u];
}
}
是不是不算很难呐~
操作2:Cut
顾名思义,Cut就是切断原树中的一条边。下面代码中,Cut(u)表示切断u和父亲的连边。这道题是有根树,非常简单——先Access(u),使u和跟节点处在同一平衡树中,然后完全切断u向fa[u]连的那条边,即使得“父子互不相认”即可。
void cut(int u){
access(u);
splay(u);
fa[ls[u]] = 0, ls[u] = 0;
upt(u);
}
操作3:Link
顾名思义,Link就是绿帽子林克将两个节点连到一起,即在原树中加边的操作。
这道题是有根树,有根树中Link操作非常简单:Link(u, v)表示把u作为v的儿子——那么直接令fa[u] = v即可。
void link(int u, int v){
cut(u);void cut(int u){
access(u);
splay(u);
fa[ls[u]] = 0, ls[u] = 0;
upt(u);
}
fa[u] = v;
}
有根树LCT涉及的基本操作只有这三条!只要写个splay、再写这三个函数,BZOJ 2002 弹飞绵羊这道题就很好写啦!
附上我的代码(大部分是Copycat企鹅学长的……)
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
#define enter putchar(\'\\n\')
#define space putchar(\' \')
template <class T>
void read(T &x){
char c;
bool op = 0;
while(c = getchar(), c > \'9\' || c < \'0\')
if(c == \'-\') op = 1;
x = c - \'0\';
while(c = getchar(), c >= \'0\' && c <= \'9\')
x = x * 10 + c - \'0\';
if(op) x = -x;
}
template <class T>
void write(T x){
if(x < 0) putchar(\'-\'), x = -x;
if(x >= 10) write(x / 10);
putchar(\'0\' + x % 10);
}
const int N = 200005;
int n, m, ta, tb;
int fa[N], ls[N], rs[N], sze[N];
#define isroot(u) (ls[fa[u]] != (u) && rs[fa[u]] != (u))
#define which(u) (ls[fa[u]] == (u))
void upt(int u){
sze[u] = sze[ls[u]] + sze[rs[u]] + 1;
}
void rotate(int u){
int v = fa[u], w = fa[v], b = which(u) ? rs[u]: ls[u];
if(!isroot(v)) which(v) ? ls[w] = u: rs[w] = u;
which(u) ? (ls[v] = b, rs[u] = v): (rs[v] = b, ls[u] = v);
fa[u] = w, fa[v] = u;
if(b) fa[b] = v;
upt(v), upt(u);
}
void splay(int u){
while(!isroot(u)){
if(!isroot(fa[u])){
if(which(u) == which(fa[u])) rotate(fa[u]);
else rotate(u);
}
rotate(u);
}
}
void access(int u){
int v = 0;
while(u){
splay(u);
rs[u] = v;
upt(u);
v = u, u = fa[u];
}
}
void cut(int u){
access(u);
splay(u);
fa[ls[u]] = 0, ls[u] = 0;
upt(u);
}
void link(int u, int v){
cut(u);
fa[u] = v;
}
int main(){
read(n);
for(int i = 1; i <= n; i++)
read(ta), sze[i] = 1, fa[i] = ta + i > n ? 0 : ta + i;
read(m);
while(m--){
read(ta);
if(ta == 1){
read(ta), ta++;
access(ta);
splay(ta);h
write(sze[ls[ta]] + 1), enter;
}
else{
read(ta), read(tb), ta++;
link(ta, ta + tb > n ? 0 : ta + tb);
}
}
return 0;
}