2.1数制与编码

Posted 2020-10-18 Lamfai

1、进位计数法

　　进位计数法是一种计数的方法。常见的进位计数法有十进制数、二进制数、十六进制数、八进制数等。十进制数是人们在日常生活中最常使用的，而在计算机中通常使用二进制数、八进制数和十六进制数。

　　在进位计数法中，每个数位所用到的不同数码的个数称为基数。十进制的基数为10（0-9），每个数位计满10就向高位进位，即“逢十进一”。

　　十进制数101，其个位的1显然与百位的1所表示的数值是不一样的。每个数码所表示的数值等于该数码本身乘以一个与它所在数位有关的常数，这个常数称为位权。一个进位数的数值大小就是它的各位数码按权相加。

　　一个r进制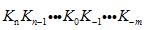（）的数值可表示为

　　　　

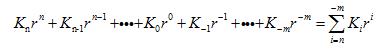
　　式中，r是基数，rⁱ是第i位的位权（整数位最低位规定为第0位）；K_i的取值可以使0,1，…，r-1共r个数码中的任意一个。

（1）二进制数

　　计算机中用的最多的是基数为2的计数制，即二进制。二进制只有0和1两种数字符号，计数“逢二进一”。它的任意数位的权为2ⁱ，i为所在位数。

（2）八进制数

　　八进制作为二进制的一种书写形式，其基数为8，有0~7共8个不同的数字符号，基数“逢八进一”。因为r=8=2³，所以只要把二进制中的3位数码编为一组就是以为八进制数，两者之间的转换极为方便。

（3）十六进制数

　　十六进制也是二进制的一种书写形式，其基数为16，“逢十六进一”。每个数位可取0~9、A、B、C、D、E、F中的任意一个，其中A、B、C、D、E、F分别表示10~15，因为r=16=2⁴，所以4位二进制数码与1位十六进制数码相对应。

2、不同进制数之间的相互转换

（1）二进制转换成八进制和十六进制

　　对于一个二进制混合数（既包含整数部分，又包含小数部分），在转换时应以小数点为界。其整数部分，从小数点开始往左数，将一串二进制分为3位（八进制）一组或4位（十六进制）一组，在数的最左边可根据需要加“0”补齐；对于小数部分，从小数点开始往右数，也将一串二进制分为3位一组或4位一组，在数的最右边也可根据需要加“0”补齐。最终使总的位数成为3或者4的整数倍，然后分别用对应的八进制或者十六进制数取代。

　　如，将二进制数1111000010.01101分别转成八进制数和十六进制数。

　　　  1　　 7　　0　　2　　　.　　　3　　2　　　　　　　　　　　　　　　　　3　　　C　　 2　　　.　　  　6　　　8

　  　　↓　　  ↓　　↓　　↓　　　↓　　　↓　　↓　　　　　　　　　　　　　　　　　↓　　　↓　　  ↓　　　↓　　　  ↓　　　↓

　　　001　111　000　010　分界点　011　010　　　　　　　　　　　　　　　　0011　1100　0010　分界点　0110　1000

　　　  ↑　　　　　　　　　　　　　　　　　↑　　　　　　　　　　　　　　　　　 ↑　　　　　　　　　　　　　　　　　↑

高位补0，凑足3位　　　　　　　　　　低位补0，凑足3位　　　　　　　　高位补0，凑足4位　　　　　　　　　　低位补0，凑足4位

　　所以，对应的八进制数为（1702.32）8=（1111000010.01101）2，　　　　　　对应的十六进制为（3C2.68）₁₆=（111000010.01101）₂

　　同样，由八进制转换成二进制只需要将每一位改为3位或者4位二进制即可（必要时去掉整数最高位或者小数最低位的0）。

　　八进制和十六进制之间的转换先转化成二进制。

（2）任意进制转换成十进制

　　将任意进制的数各位数码与它们的权重相乘，再把乘积相加，就得到了一个十进制数。这种方法称为按权展开相加法。

　　如，（11011.1）₂=1×2⁴+1×2³+0×2²+1×2¹+1×2⁰+1×2^-1=27.5

（3）十进制转换成任意进制

　　一个十进制数转换成任意进制数，常采用基数乘除法。这种转换方法对十进制数的整数部分和小数部分将分别进行处理，对于整数部分采用除基取余法；对于小数部分采用乘基取整法，最后将整数部分和小数部分的转换结果拼接起来。

　　除基取余法（整数部分的转换）：整数部分除基取余，最先取得的余数为数的最低位，最后取得的余数为数的最高位（即除基取余，先余为低，后余为高），商为0时结束。

　　如，将123.6875转换成二进制数

　　整数部分

　　

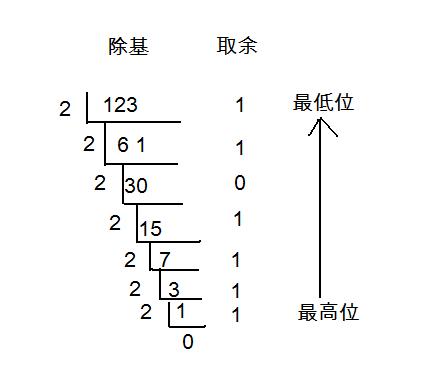
　　所以，整数部分　123=（1111011）₂

　　乘基取整法（小数部分的转换）：小数部分乘基取整，最先得到的整数为数的最高位，最后取得的整数为数的最低位（即乘基取整。先整为高，后整为低），乘积为0（或满足精度要求）时结束。

　　小数部分

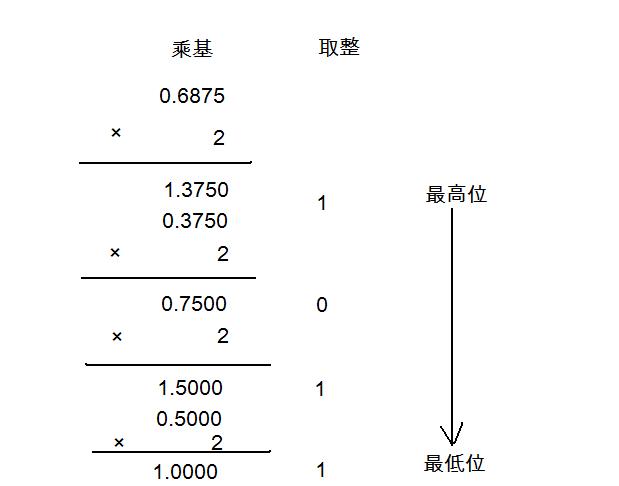
　　所以小数部分为0.678=（0.1011）₂

2、真值和机器数

　　在日常生活中，通常用正、负号来分别表示正数（正号可省略）、负数，如+15、-8等。这种带“+”或“-”符号的数称为真值。真值是机器数所代表的实际值。

　　在计算机中，通常采用数的符号和数值一起编码的方法来表示数据。常用的有=原码、补码和放码表示法。这几种表示法都将数据的符号数字化。通常采用“0”表示“正”，用“1”表示“负”，如0,101（这里的都好“，”实际上并不存在，仅为区分符号位与数值位）表示+5。这种把符号“数字化”的数称为机器数。

3、BCD码

　　二进制编码的十进制数（BCD）通常采用4位二进制来表示一位十进制数中的0~9这10个数码。

（1）8421码（最常用）

　　它是一种有权码，设其各位的数值位b₃、b₂、b₁、b₀，则权值从高到底依次为8、4、2、1，则它表示的数为D=8b₃+4b₂+2b₁+1b₀，如8→1000；9→1001

（2）余3码

（3）2421码