k均值聚类

Posted 2020-10-18 WHLOOK

1.k均值聚类是聚类算法，不是分类算法

k均值聚类就是利用欧氏距离的度量将距离相近的样本分为k类

2.算法思想

a. 假设有m个样本，{[x1,y1],[x2,y2],,,,[xm,ym]}，首先随机选择k个样本作为聚类的质心（要分成k类）

b. 然后对于每个样本，计算它到每个质心的距离，将它归类于距离最小的那个质心

c. 接着对初步分类的k个类别重新计算该类的质心，也就是对每个类别的样本坐标求平均

d. 重复 b 步和 c 步直到质心的坐标不再改变或者变化小于设定值

3.Matlab程序示例

%生成原始数据
clear;
x=zeros(100,2);
x(1:30,1:2)=randn(30,2);
x(31:70,1:2)=5+randn(40,2);
x(71:100,1:2)=10+randn(30,2);

plot(x(:,1),x(:,2),\'g*\') % 显示原始样本数据图
hold on;

k = 3; %聚类数
[m,n] = size(x); %获得样本数和维度
pre_centroids = x(randi(100,k,1),:); %初始的随机质心

plot(pre_centroids(:,1),pre_centroids(:,2),\'bo\'); %画出初始质心

figure
hold on;
plot(x(:,1),x(:,2),\'g*\')

sum_ = zeros(k,n); % 用来储存每个类别样本的坐标累加和
num_ = zeros(k,1); % 用来记录每个类别中的样本个数

while 1
    for i=1:m
        dis = [];
        %对于每个样本，计算它到每个质心的距离
        for j = 1:k
            dis(j) = sum((x(i,:)-pre_centroids(j,:)).^2);
        end

        [min_dis,min_idx] = min(dis); % 找到距离最小的那个质心的索引
        sum_(min_idx,:) = sum_(min_idx,:)+ x(i,:);%累加每个类的样本的坐标
        num_(min_idx,:) = num_(min_idx,:)+1;%类别中的样本数累加
    end

    for i=1:k
        centroids(i,:) = sum_(i,:)./num_(i,:); %重新计算质心
    end

    if norm(centroids-pre_centroids)<0.001 %退出迭代的条件
        break;
    end

    pre_centroids = centroids; %更新质心
end

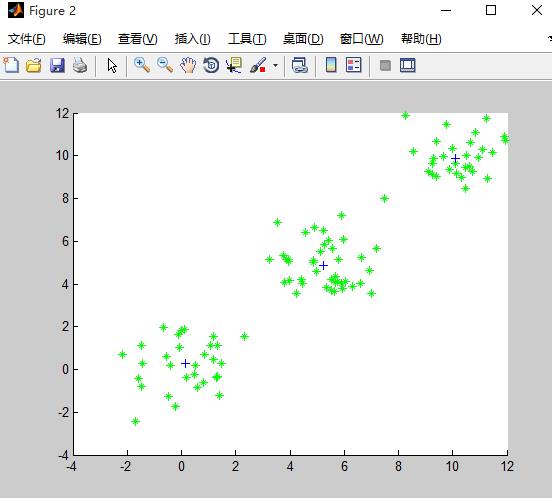
plot(pre_centroids(:,1),pre_centroids(:,2),\'b+\'); %输出聚类后的图

4.实验结果

初始的随机质心：

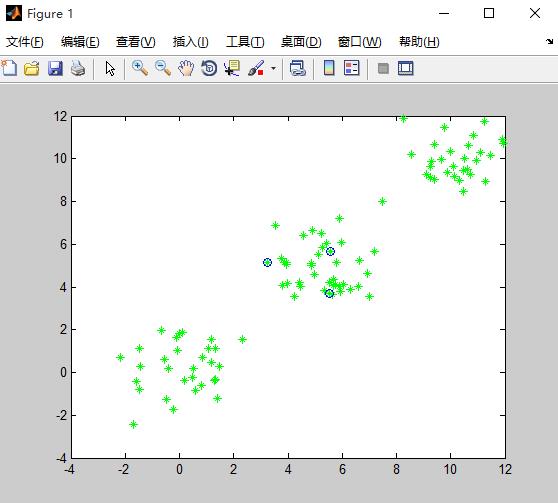
聚类后的质心：