Description
The network consists of two parts: part A and part B. Each part consists of n vertices; i-th vertex of part A is denoted as Ai, and i-th vertex of part B is denoted as Bi.
For each index i (1 ≤ i < n) there is a directed edge from vertex Ai to vertex Ai + 1, and from Bi to Bi + 1, respectively. Capacities of these edges are given in the input. Also there might be several directed edges going from part A to part B (but never from B to A).
You have to calculate the maximum flow value from A1 to Bn in this network. Capacities of edges connecting Aito Ai + 1 might sometimes change, and you also have to maintain the maximum flow value after these changes. Apart from that, the network is fixed (there are no changes in part B, no changes of edges going from A to B, and no edge insertions or deletions).
Take a look at the example and the notes to understand the structure of the network better.
Input
The first line contains three integer numbers n, m and q (2 ≤ n, m ≤ 2·105, 0 ≤ q ≤ 2·105) — the number of vertices in each part, the number of edges going from A to B and the number of changes, respectively.
Then n - 1 lines follow, i-th line contains two integers xi and yi denoting that the edge from Ai to Ai + 1 has capacity xi and the edge from Bi to Bi + 1 has capacity yi (1 ≤ xi, yi ≤ 109).
Then m lines follow, describing the edges from A to B. Each line contains three integers x, y and z denoting an edge from Ax to By with capacity z (1 ≤ x, y ≤ n, 1 ≤ z ≤ 109). There might be multiple edges from Ax to By.
And then q lines follow, describing a sequence of changes to the network. i-th line contains two integers vi and wi, denoting that the capacity of the edge from Avi to Avi + 1 is set to wi (1 ≤ vi < n, 1 ≤ wi ≤ 109).
Output
Firstly, print the maximum flow value in the original network. Then print q integers, i-th of them must be equal to the maximum flow value after i-th change.
input
4 3 2
1 2
3 4
5 6
2 2 7
1 4 8
4 3 9
1 100
2 100
output
9
14
14
Note
This is the original network in the example:
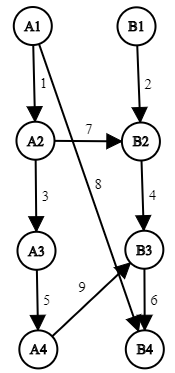
solution:
显然2e5的大小不能用最大流来做,我们观察到该网络A与B部分除去中间的边是两条链
那么我们可以转而求最小割
我们每一次求最小割一定是取A的x与B的y点的出边割去,并把u <= x && v > y 的中间的边割去
我们只会修改A一侧的权值,所以可以用线段树维护。
#include <cstdio> #include <iostream> #include <cstring> #define mid ((L + R) >> 1) #define travel(x, i) for (int i = fir[x]; i; i = e[i].nxt) #define rep(i, x, y) for (register int i = (x); i <= (y); i ++) using namespace std; typedef long long LL; const int N = 2e5 + 5; const LL INF = 1e16; struct edge { int nxt, to, cap; } e[N]; int fir[N], cnt = 0; int A[N], B[N]; int n, m, q; LL key[N << 2], lazy[N << 2], tab[N]; inline void addedge(int x, int y, int c) { e[++ cnt] = (edge){fir[x], y, c}; fir[x] = cnt; } inline void Down(int x) { if (!lazy[x]) return; key[x << 1] += lazy[x]; key[x << 1 | 1] += lazy[x]; lazy[x << 1] += lazy[x]; lazy[x << 1 | 1] += lazy[x]; lazy[x] = 0; } inline void Modify(int p, LL val, int x = 1, int L = 1, int R = n + 1) { if (L == R) { key[x] = val; return; } Down(x); if (p <= mid) Modify(p, val, x << 1, L, mid); else Modify(p, val, x << 1 | 1, mid + 1, R); key[x] = min(key[x << 1], key[x << 1 | 1]); } inline void Add(int r, LL val, int x = 1, int L = 1, int R = n + 1) { if (R <= r) { key[x] += val; lazy[x] += val; return; } Down(x); Add(r, val, x << 1, L, mid); if (mid < r) Add(r, val, x << 1 | 1, mid + 1, R); key[x] = min(key[x << 1], key[x << 1 | 1]); } int main() { int x, y, w; scanf("%d%d%d", &n, &m, &q); Modify(n + 1, INF); rep(i, 2, n) { scanf("%d%d", &A[i], &B[i]); Modify(i, B[i]); } rep(i, 1, m) { scanf("%d%d%d", &x, &y, &w); addedge(x, y, w); } rep(i, 1, n) { travel(i, j) Add(e[j].to, e[j].cap); tab[i + 1] = key[1]; } memset(key, 0, sizeof key); memset(lazy, 0, sizeof lazy); Modify(1, INF); rep(i, 2, n + 1) Modify(i, tab[i] + A[i]); printf("%lld\n", key[1]); rep(i, 1, q) { scanf("%d%d", &x, &w); x ++; A[x] = w; Modify(x, tab[x] + A[x]); printf("%lld\n", key[1]); } return 0; }