毕达哥拉斯树(pythagorasTree)原理解析及canvas动画实现

Posted 2020-10-18 Grewer

以前就看到了这个东西,由于太忙了最近才有时间来实现这个;

该文章适合有一定 canvas 基础的人阅读;

首先说说他的原理:

The construction of the Pythagoras tree begins with a square. Upon this square are constructed two squares, each scaled down by a linear factor of ½√2, such that the corners of the squares coincide pairwise. The same procedure is then applied recursively to the two smaller squares, ad infinitum. The illustration below shows the first few iterations in the construction process.

 

Order 0	Order 1	Order 2	Order 3

以上文字和图像摘自维基百科:https://en.wikipedia.org/wiki/Pythagoras_tree_(fractal)

大意是先有一个正方形,然后在他的上方构建2个正方形,使他们三条边构成一个三角形,再向上蔓延,循环往复,直至无穷;

当然我们是不可能做无穷的,这样很容易崩溃的;

先写上代码,我做了比较详细的注释:

首先制作背景及一些条件的确定:

 

var Init = function() {
    var canvas = document.getElementById(\'canvas\');
    this.ctx = canvas.getContext(\'2d\');

    this.vw = canvas.width = window.innerWidth;
    this.vh = canvas.height = window.innerHeight; //定义 canvas大小
    this.boxSize = 80; //树的大小

    this.maxLevel = 6; //树的节数
    this.color1 = { h: 70, s: 75, l: 51 }; //树顶颜色 青绿色
    this.color2 = { h: 310, s: 98, l: 17 }; //树根颜色 咖啡色
    // HSL色彩模式：就是色调(Hue)、饱和度(Saturation)、亮度(Lightness)三个颜色通道的改变以及它们相互之间的叠加来获得各种颜色，色调(Hue)色调最大值360，饱和度和亮度有百分比表示0-100%之间。
    // H：
    // Hue(色调)。0(或360)表示红色，120表示绿色，240表示蓝色，也可取其他数值来指定颜色。取值为：0 - 360
    // S：
    // Saturation(饱和度)。取值为：0.0% - 100.0%
    // L：
    // Lightness(亮度)。取值为：0.0% - 100.0%
    // 当然这里 rgb 肯定也是可以的

    this.mouse = {
        x: this.vw / 2,
        y: this.vh / 2
    }; //默认鼠标位置 屏幕中心

    this.lean = 0; //三角形顶点左右偏移程度
    this.scale = 0; //三角形高度比例

    this.x = (this.vw - this.boxSize) / 2;
    //x 时候从浏览器左边开始到树根左边的长度 同样的也是 浏览器右边到树根右边的长度
    this.y = this.vh;

    this.getColors(this.color1, this.color2, this.maxLevel + 1);
    //取色,将颜色从 color1到 color 2 平均分成 maxLevel+1 种,你可以加3,加4 因为 maxLeval 不足的话有一部分颜色计算出来是白色会与白色背景冲突
}

 

上部有 getColor 函数,现在我们来定义他,他的作用是返回一个用来存储颜色的数组,颜色是根据上述的 color1和 color2 还有this.maxlevel 来确定的;

循环 maxlevel 来分离出这两种颜色之间的不同色差;

Init.prototype.getColors = function(c1, c2, steps) {
    this.colors = [];
    var lerp = this.methods.lerp;
    for (let i = 0; i < steps; i++) {
        const t = i / (steps - 1);
        const h = Math.round(lerp(c1.h, c2.h, t));
        const s = Math.round(lerp(c1.s, c2.s, t));
        const l = Math.round(lerp(c1.l, c2.l, t));

        this.colors.push(\'hsl(\'+h+\',\'+s+\'%,\'+l+\'%)\');
    }
}

 

 再是绘制出树根的代码,他是根据 size ,scale,lean,level 即,正方形的边长,构成三角形的高的比例,三角形的顶点的左右偏移,还有 level 即上部代码的颜色等级;

他的执行顺序是先绘制左边的正方形,在绘制右边的;

Init.prototype.drawTree = function(size, scale, lean, level) {
    //最初值80 0.4 0 5
    //长度,弯曲度,倾斜度,颜色域
    var ctx = this.ctx;
    var constitute = this.calcBranches(size, scale, lean);
    //获取构成三角形的边长和角度

    ctx.save(); //因为倾斜的角度是不一样的,所以需要存储
    ctx.fillRect(0, 0, size, -size); //构成三角形的绘出正方形,初始是树根的位置

    ctx.fillStyle = this.colors[level]; //填充树的颜色

    ctx.translate(0, -size); //改变canvas的坐标位置 ,移至正方形左上角
    ctx.rotate(-constitute.leftAngle); //根据一个角度对图像进行旋转,负值代表向左倾斜

    if (level) {
        this.drawTree(constitute.leftSize, scale, lean, level - 1);
    } else {
        ctx.fillRect(0, 0, constitute.leftSize, -constitute.leftSize);
        //最后一种颜色,递归结束
    }
    //根据颜色域,来递归进行渲染三角形 直至颜色用完

    ctx.translate(constitute.leftSize, 0); //改变坐标  横坐标移至左边正方形的右下角
    ctx.rotate(constitute.rightAngle + constitute.leftAngle); //旋转
    //渲染右边的正方形,rotate 是整个绘图都会旋转,因为刚刚 rotate(-leftAngle),所以加上 leftAngle 是让整个图像变成水平,再根据 rightAngle 进行右旋转
    if (level) {
        this.drawTree(constitute.rightSize, scale, lean, level - 1);
    } else {
        ctx.fillRect(0, 0,constitute.rightSize, -constitute.rightSize);
    } //递归绘制右正方形

    ctx.restore();
}

 上述代码中有一个函数为calcBranches 这是最为关键的代码,他的只要作用是通过计算得出下一个绘制的正方形的边长,角度,顺便将他们存储起来,减缓浏览器的压力;

关于缓存,是通过闭包来实现的:

一个简单的例子就是:

var fun1 = (function (){
    var arr = [];
    var fun2 = function(){
    arr.push( (new Date()).valueOf() )      
  }
    return fun2;
})()

 

 这段代码执行的时候 fun1 当即会执行一遍,这样就会出现一个 arr 变量,但是这个变量并不会暴露出来;

但是而每当调用fun1(fun2)时便会对 arr 作出改变,这便是缓存的原理;

calcBranches代码:

Init.prototype.calcBranches = (function() {
    var cache = {};

    var memoize = function(width, scale, lean) {
        //长度,三角形高度比例,倾斜度 初始值 80 0.4 0
        //lean 范围 -0.5 到0.5 lean接近0.5时 左树枝几乎为0 同理 -.5时 有树枝几乎为0 即构成三角形皆为直角三角形
        var memoKey = width+\'-\'+scale+\'-\'+lean;
        if (!cache[memoKey]) {
            //存储这三个值,形成缓存,减少绘制压力
            var currentH = width * scale; //当前高度即构成三角形对于正方形的高度

            var result = {
                leftSize: Math.sqrt(currentH ** 2 + (width * (0.5 - lean)) ** 2),
                rightSize: Math.sqrt(currentH ** 2 + (width * (0.5 + lean)) ** 2),
                leftAngle: Math.atan(currentH / ((0.5 - lean) * width)),
                rightAngle: Math.atan(currentH / ((0.5 + lean) * width))
            };
            //**表示几次方 
            //关键代码,根据当前的长度
            //初始化时  第一个width = boxSize;
            //leftSize 构成三角形的左边长
            //rightSize 右边长
            //leftAngle 左边的角度的反正切值  -PI/2 到 PI/2 之间的弧度值。 是一个角度
            //rightAngle 右边的角度的反正切值 同上
            cache[memoKey] = result;
        }
        return cache[memoKey];

    }
    memoize.cache = cache;
    return memoize;
})();//通过闭包实现缓存;

 

 

 再就是渲染函数,他的主要作用就是绘制初始图形,并且通过计算得出需要绘制的正方形的 scale,lean 这2个关键影响因素;

他们之间的关系你可以自己随便改;

Init.prototype.render = function(){
    var map = this.methods.map,
        ctx = this.ctx
    var scale = map(this.mouse.y, this.vh, 0, 0, 0.8)
    //通过 map函数得出高的比例 主要来源鼠标 y 的值

    var lean = map(this.mouse.x, 0,this.vw, 0.5, -0.5)
    //通过 map函数得出左右倾斜程度 只要影响:鼠标 x 的值


    ctx.clearRect(0,0,this.vw,this.vh)//清空画布

    ctx.save(); //因为颜色会渐变,所以需要使用 save 存储为染色前的状态
    ctx.fillStyle = this.colors[this.maxLevel];
    //树根颜色
    ctx.translate(this.x,this.y); //将 canvas 坐标移动到 x,0  x 是树根左边距浏览器左边的长度

    this.drawTree(this.boxSize, scale, lean,this.maxLevel); //绘制初始树

    ctx.restore();

    requestAnimationFrame(this.render.bind(this));
}

 

他们之间所用的函数, lerp,map都是纯函数,即当输入的数是不变的情况下,不管输入几次他的输出都是固定的,即没有随机数的影响,比如时间戳等等;

Init.prototype.methods = {
    //pure function
    lerp: function lerp(a, b, t) {
        return a + (b - a) * t;
    },
    map:function map(x, a, b, c, d) {
        return c + (d - c) * ((x - a) / (b - a)) || 0;
    }
}

 

最后一步, new 出对象,进行 render ,再添加监听鼠标移动事件:

var init = new Init();
init.render();
window.addEventListener("mousemove", function(event) {
    init.mouse.x = event.clientX;
    init.mouse.y = event.clientY;

});

 基本过程便是这样;

 

部分代码我也是从网上获取灵感;

我的 demo 中

这个是最基本的构成;最底下的我取名树根;在上部是树枝;

再是:

 

 该红色的高就是根据鼠标的高度来生成的即代码中的currentH;

　　

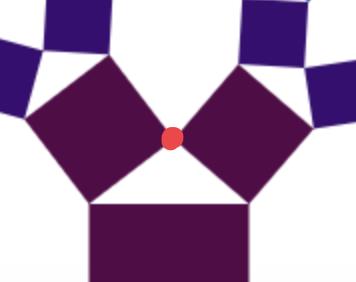
关于该红色的点的定位主要由鼠标位置和网页大小组成的;代码中的scale决定该点的上下高度(主要受鼠标纵坐标影响),即上面所说的高,而 lean 决定该点的左右坐标(主要受鼠标横坐标影响);

demo地址:https://grewer.github.io/JsDemo/pythagorasTree/pythagorasTree.html

github:https://github.com/Grewer/JsDemo/blob/master/pythagorasTree/pythagorasTree.html

希望大家能给个推荐或 star ,十分感谢!

完;