上图
图片来自维基百科·自由的百科全书
最近在尝试做一些流量调控的事情,流量对于任何商业系统都是宝贵的资源,不能任由他人无限制获取,且需要通过一定手段加以调控,以期用户体验、平台生态、平台利益多方最大化。
这个目标是宏大而美好的,但总要一步步慢慢来。先说如何平衡生态问题(当然指的是B端用户),生态问题就像国民收入均衡问题一样,常用的就是基尼系数,维基百科的中文链接要FQ才能打开,好伤心,英文的我这里能打开。这里我并不要介绍概念和定义,只想把如何计算的方法贴上来。
最直观的计算公式是:
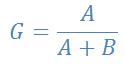
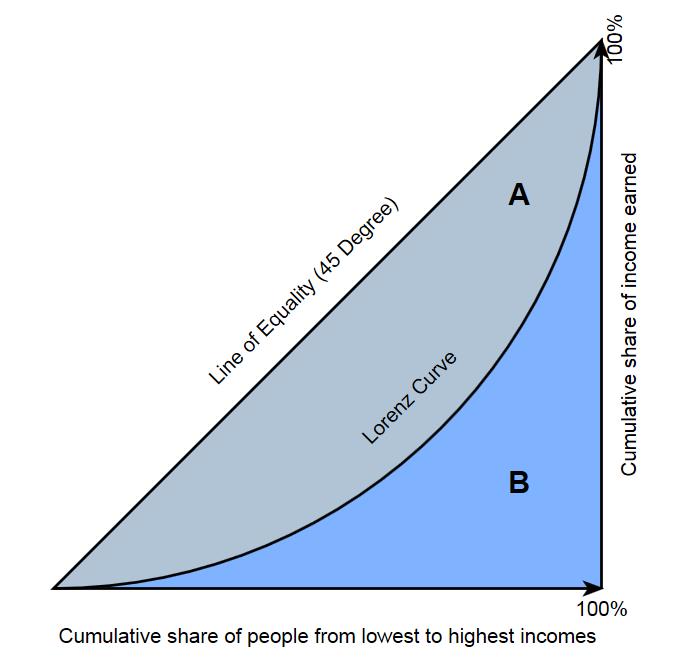
含义就是:把所有人(假设刚好 100 个人)的收入从小到大排序,然后从收入最少的开始累计,每计算一个人,横坐标为人数累计值占总人数比例,纵坐标为收入累计值占总收入比例,直到最后一个收入最大的人。
显然,图中横坐标和纵坐标都是 [ 0 -1 ] 之间。把图左下角和右上角连起来,表示人数累计占比恒等于收入累积占比,意味着收入完全均等。
好了,上面人人收入均等的线与实际收入曲线之间的面积就是 A, 实际收入曲线与 X 轴之间面积是 B。
知道怎么算了,于是拿代码试试:
# coding=utf-8
# !/usr/bin/python
from scipy.integrate import odeint
import numpy as np
from matplotlib import pyplot as pl
# 解决matplotlib 中文显示问题
pl.rcParams[\'font.sans-serif\'] = [\'SimHei\']
pl.rcParams[\'axes.unicode_minus\'] = False
fig, ax = pl.subplots()
# 计算基尼系数的简单方法
def gini():
# 计算数组累计值,从 0 开始
wealths = [1.5, 2, 3.5, 10, 4.2, 2.1, 1.1, 2.2, 3.1, 5.1, 9.5, 9.7, 1.7, 2.3, 3.8, 1.7, 2.3, 5, 4.7, 2.3, 4.3, 12]
cum_wealths = np.cumsum(sorted(np.append(wealths, 0)))
# 取最后一个,也就是原数组的和
sum_wealths = cum_wealths[-1]
# 人数的累积占比
xarray = np.array(range(0, len(cum_wealths))) / np.float(len(cum_wealths) - 1)
# 均衡收入曲线
upper = xarray
# 收入累积占比
yarray = cum_wealths / sum_wealths
# 绘制基尼系数对应的洛伦兹曲线
ax.plot(xarray, yarray)
ax.plot(xarray, upper)
ax.set_xlabel(u\'人数累积占比\')
ax.set_ylabel(u\'收入累积占比\')
pl.show()
# 计算曲线下面积的通用方法
B = np.trapz(yarray, x=xarray)
# 总面积 0.5
A = 0.5 - B
G = A / (A + B)
print G
得到下图
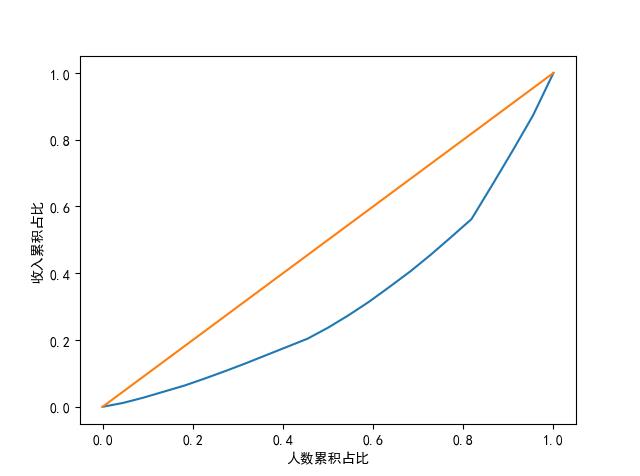
其他
当然还有很多其他的公式可以计算,比如:
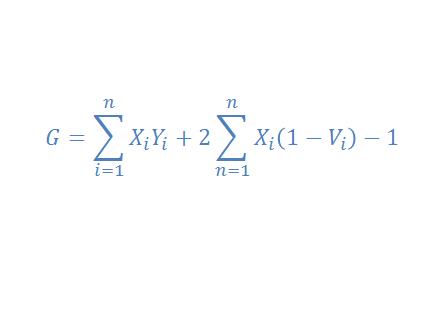
参考
- https://en.wikipedia.org/wiki/Gini_coefficient 基尼系数定义
- https://www.zhihu.com/question/25404709 matplotlib 绘图中文乱码
- http://hyry.dip.jp/tech/book/page/scipynew/scipy-710-integrate.html python 科学计算