Deep Learning之线性单元和梯度下降

Posted 2020-10-17 Ariel_一只猫的旅行

 

往期回顾

 在上一篇文章中，我们已经学会了编写一个简单的感知器，并用它来实现一个线性分类器。你应该还记得用来训练感知器的『感知器规则』。然而，我们并没有关心这个规则是怎么得到的。本文通过介绍另外一种『感知器』，也就是『线性单元』，来说明关于机器学习一些基本的概念，比如模型、目标函数、优化算法等等。这些概念对于所有的机器学习算法来说都是通用的，掌握了这些概念，就掌握了机器学习的基本套路。

线性单元是什么？

感知器有一个问题，当面对的数据集不是线性可分的时候，『感知器规则』可能无法收敛，这意味着我们永远也无法完成一个感知器的训练。为了解决这个问题，我们使用一个可导的线性函数来替代感知器的阶跃函数，这种感知器就叫做线性单元。线性单元在面对线性不可分的数据集时，会收敛到一个最佳的近似上。

为了简单起见，我们可以设置线性单元的激活函数f为：

这样的线性单元如下图所示：

对比此前我们讲过的感知器

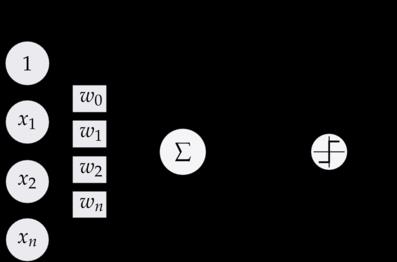
这样替换了激活函数f之后，线性单元将返回一个实数值而不是0、1分类。因此线性单元用来解决回归问题而不是分类问题。

线性单元的模型

当我们说模型时，我们实际上在谈论根据输入x预测输出y的算法。比如，x可以是一个人的工作年限，y可以是他的月薪，我们可以用某种算法来根据一个人的工作年限来预测他的收入。比如：

你也许会说，这个模型太不靠谱了。是这样的，因为我们考虑的因素太少了，仅仅包含了工作年限。如果考虑更多的因素，比如所处的行业、公司、职级等等，可能预测就会靠谱的多。我们把工作年限、行业、公司、职级这些信息，称之为特征。对于一个工作了5年，在IT行业，百度工作，职级T6这样的人，我们可以用这样的一个特征向量来表示他

x = (5, IT, 百度, T6)。

监督学习和无监督学习

接下来，我们需要关心的是这个模型如何训练，也就是参数w取什么值最合适。

机器学习有一类学习方法叫做监督学习，它是说为了训练一个模型，我们要提供这样一堆训练样本：每个训练样本既包括输入特征x，也包括对应的输出y(y也叫做标记，label)。也就是说，我们要找到很多人，我们既知道他们的特征(工作年限，行业...)，也知道他们的收入。我们用这样的样本去训练模型，让模型既看到我们提出的每个问题(输入特征x)，也看到对应问题的答案(标记y)。当模型看到足够多的样本之后，它就能总结出其中的一些规律。然后，就可以预测那些它没看过的输入所对应的答案了。

另外一类学习方法叫做无监督学习，这种方法的训练样本中只有x而没有y。模型可以总结出特征x的一些规律，但是无法知道其对应的答案y。

很多时候，既有x又有y的训练样本是很少的，大部分样本都只有x。比如在语音到文本(STT)的识别任务中，x是语音，y是这段语音对应的文本。我们很容易获取大量的语音录音，然而把语音一段一段切分好并标注上对应文字则是非常费力气的事情。这种情况下，为了弥补带标注样本的不足，我们可以用无监督学习方法先做一些聚类，让模型总结出哪些音节是相似的，然后再用少量的带标注的训练样本，告诉模型其中一些音节对应的文字。这样模型就可以把相似的音节都对应到相应文字上，完成模型的训练。

线性单元的目标函数

现在，让我们只考虑监督学习。

我们还可以把上面的式子写成和式的形式。使用和式，书写起来简单。所以写成下面这样：

其中

梯度下降优化算法

不过对于计算机来说，它可不会解方程。但是它可以凭借强大的计算能力，一步一步的去把函数的极值点『试』出来。如下图所示：

你可能要问了，为何每次修改x的值，都能往函数最小值那个方向前进呢？这里的奥秘在于，我们每次都是向函数y=f(x)的梯度的相反方向来修改x。

那么什么是梯度呢？翻开大学高数课的课本，我们会发现梯度是一个向量，它指向函数值上升最快的方向。

显然，梯度的反方向当然就是函数值下降最快的方向了。我们每次沿着梯度相反方向去修改x的值，当然就能走到函数的最小值附近。之所以是最小值附近而不是最小值那个点，是因为我们每次移动的步长不会那么恰到好处，有可能最后一次迭代走远了越过了最小值那个点。

步长的选择是门手艺，如果选择小了，那么就会迭代很多轮才能走到最小值附近；如果选择大了，那可能就会越过最小值很远，收敛不到一个好的点上。

按照上面的讨论，我们就可以写出梯度下降算法的公式：

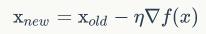
对于上一节列出的目标函数(式2)

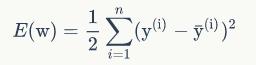
梯度下降算法可以写成：

聪明的你应该能想到，如果要求目标函数的最大值，那么我们就应该用梯度上升算法，它的参数修改规则是：

因此，线性单元的参数修改规则最后是这个样子：

 

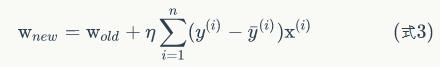
有了上面这个式子，我们就可以根据它来写出训练线性单元的代码了。

如果您还是没看明白，建议您也吐血再看一下大学时学过的《线性代数》吧。

这一节你尽可以跳过它，并不太会影响到全文的理解。当然如果你非要弄明白每个细节，那恭喜你骚年，机器学习的未来一定是属于你的。

首先，首先简单做一下前戏介绍。我们知道函数梯度的定义就是它相对于各个变量的偏导数，所以我们写下下面的式子

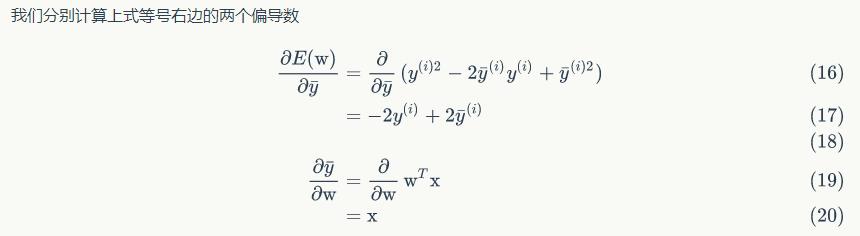
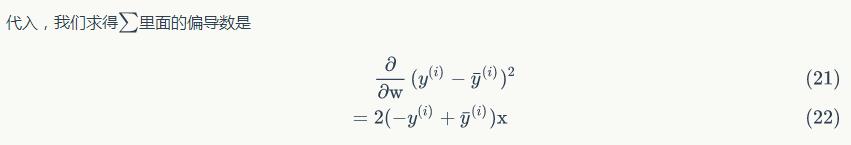
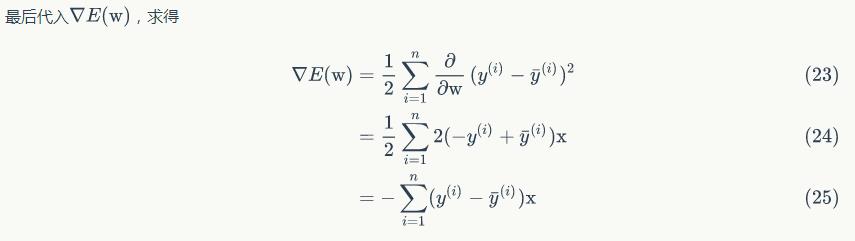
至此，大功告成。

随机梯度下降算法(Stochastic Gradient Descent, SGD)

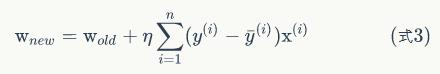
如果我们根据(式3)来训练模型，那么我们每次更新w的迭代，要遍历训练数据中所有的样本进行计算，我们称这种算法叫做批梯度下降(Batch Gradient Descent)。如果我们的样本非常大，比如数百万到数亿，那么计算量异常巨大。因此，实用的算法是SGD算法。

在SGD算法中，每次更新w的迭代，只计算一个样本。这样对于一个具有数百万样本的训练数据，完成一次遍历就会对w更新数百万次，效率大大提升。---请多加理解这段话。

由于样本的噪音和随机性，每次更新w并不一定按照减少E的方向。然而，虽然存在一定随机性，大量的更新总体上是沿着减少E的方向前进的，因此最后也能收敛到最小值附近。下图展示了SGD和BGD的区别：

如上图，椭圆表示的是函数值的等高线，椭圆中心是函数的最小值点。红色是BGD的逼近曲线，而玫红色是SGD的逼近曲线。我们可以看到BGD是一直向着最低点前进的，而SGD明显躁动了许多，但总体上仍然是向最低点逼近的。

最后需要说明的是，SGD不但效率高，而且随机性有时候反而是好事。今天的目标函数是一个『凸函数』，沿着梯度反方向就能找到全局唯一的最小值。然而对于非凸函数来说，存在许多局部最小值。随机性有助于我们逃离某些很糟糕的局部最小值，从而获得一个更好的模型。

实现线性单元

完整代码请参考GitHub: https://github.com/hanbt/learn_dl/blob/master/linear_unit.py (python2.7)

因为我们已经写了感知器的代码，因此我们先比较一下感知器模型和线性单元模型，看看哪些代码能够复用。

比较的结果令人震惊，原来除了激活函数f不同之外，两者的模型和训练规则是一样的(在上表中，线性单元的优化算法是SGD算法)。那么，我们只需要把感知器的激活函数进行替换即可。感知器的代码请参考上一篇文章，这里就不再重复了。对于一个养成良好习惯的程序员来说，重复代码是不可忍受的。大家应该把代码保存在一个代码库中(比如git)。

1 from perceptron import Perceptron
2 #定义激活函数f
3 f = lambda x: x
4 class LinearUnit(Perceptron):
5     def __init__(self, input_num):
6         \'\'\'初始化线性单元，设置输入参数的个数\'\'\'
7         Perceptron.__init__(self, input_num, f)

通过继承Perceptron，我们仅用几行代码就实现了线性单元。这再次证明了面向对象编程范式的强大。

接下来，我们用简单的数据进行一下测试。

 1 def get_training_dataset():
 2     \'\'\'
 3     捏造5个人的收入数据
 4     \'\'\'
 5     # 构建训练数据
 6     # 输入向量列表，每一项是工作年限
 7     input_vecs = [[5], [3], [8], [1.4], [10.1]]
 8     # 期望的输出列表，月薪，注意要与输入一一对应
 9     labels = [5500, 2300, 7600, 1800, 11400]
10     return input_vecs, labels    
11 def train_linear_unit():
12     \'\'\'
13     使用数据训练线性单元
14     \'\'\'
15     # 创建感知器，输入参数的特征数为1（工作年限）
16     lu = LinearUnit(1)
17     # 训练，迭代10轮, 学习速率为0.01
18     input_vecs, labels = get_training_dataset()
19     lu.train(input_vecs, labels, 10, 0.01)
20     #返回训练好的线性单元
21     return lu
22 if __name__ == \'__main__\': 
23     \'\'\'训练线性单元\'\'\'
24     linear_unit = train_linear_unit()
25     # 打印训练获得的权重
26     print linear_unit
27     # 测试
28     print \'Work 3.4 years, monthly salary = %.2f\' % linear_unit.predict([3.4])
29     print \'Work 15 years, monthly salary = %.2f\' % linear_unit.predict([15])
30     print \'Work 1.5 years, monthly salary = %.2f\' % linear_unit.predict([1.5])
31     print \'Work 6.3 years, monthly salary = %.2f\' % linear_unit.predict([6.3])

程序运行结果如下图：

拟合的直线如下图：

附完整代码：

 1 #!/usr/bin/env python
 2 # -*- coding: UTF-8 -*-
 3 
 4 from perceptron import Perceptron
 5 
 6 
 7 #定义激活函数f
 8 f = lambda x: x
 9 
10 class LinearUnit(Perceptron):
11     def __init__(self, input_num):
12         \'\'\'初始化线性单元，设置输入参数的个数\'\'\'
13         Perceptron.__init__(self, input_num, f)
14 
15 
16 def get_training_dataset():
17     \'\'\'
18     捏造5个人的收入数据
19     \'\'\'
20     # 构建训练数据
21     # 输入向量列表，每一项是工作年限
22     input_vecs = [[5], [3], [8], [1.4], [10.1]]
23     # 期望的输出列表，月薪，注意要与输入一一对应
24     labels = [5500, 2300, 7600, 1800, 11400]
25     return input_vecs, labels    
26 
27 
28 def train_linear_unit():
29     \'\'\'
30     使用数据训练线性单元
31     \'\'\'
32     # 创建感知器，输入参数的特征数为1（工作年限）
33     lu = LinearUnit(1)
34     # 训练，迭代10轮, 学习速率为0.01
35     input_vecs, labels = get_training_dataset()
36     lu.train(input_vecs, labels, 10, 0.01)
37     #返回训练好的线性单元
38     return lu
39 
40 
41 def plot(linear_unit):
42     import matplotlib.pyplot as plt
43     input_vecs, labels = get_training_dataset()
44     fig = plt.figure()
45     ax = fig.add_subplot(111)
46     ax.scatter(map(lambda x: x[0], input_vecs), labels)
47     weights = linear_unit.weights
48     bias = linear_unit.bias
49     x = range(0,12,1)
50     y = map(lambda x:weights[0] * x + bias, x)
51     ax.plot(x, y)
52     plt.show()
53 
54 
55 if __name__ == \'__main__\': 
56     \'\'\'训练线性单元\'\'\'
57     linear_unit = train_linear_unit()
58     # 打印训练获得的权重
59     print linear_unit
60     # 测试
61     print \'Work 3.4 years, monthly salary = %.2f\' % linear_unit.predict([3.4])
62     print \'Work 15 years, monthly salary = %.2f\' % linear_unit.predict([15])
63     print \'Work 1.5 years, monthly salary = %.2f\' % linear_unit.predict([1.5])
64     print \'Work 6.3 years, monthly salary = %.2f\' % linear_unit.predict([6.3])
65     plot(linear_unit)

小结

事实上，一个机器学习算法只有两部分，即模型和目标函数：

因此，如果你想最简洁的介绍一个算法，列出这两个函数就行了。

接下来，你会用优化算法去求取目标函数的最小(最大)值。[随机]梯度{下降|上升}算法就是一个优化算法。针对同一个目标函数，不同的优化算法会推导出不同的训练规则。

其实在机器学习中，算法往往并不是关键，真正的关键之处在于选取特征。选取特征需要我们人类对问题的深刻理解，经验、以及思考。而神经网络算法的一个优势，就在于它能够自动学习到应该提取什么特征，从而使算法不再那么依赖人类，而这恰是神经网络为何如此吸引人的一个方面。

Congratulations！经过漫长的烧脑，已经具备了学习神经网络的必备知识。