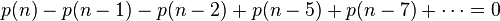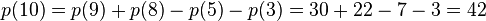转载转载转载！整数拆分问题的四种解法--尼奥普兰

Posted 2020-10-17 vectors07

整数拆分问题的四种解法

原创 2015年04月01日 21:17:09

• 标签：
• 算法 /
• 母函数定理 /
• 五边形数定理 /
• acm /
• 动态规划

 

整数划分问题是算法中的一个经典命题之一

 

所谓整数划分，是指把一个正整数n写成如下形式：

n=m1+m2+m3+....+mi;（其中mi为正整数，并且1<=mi<=n），则{m1,m2,m3,....,mi}为n的一个划分。

如果{m1,m2,m3,....,mi}中的最大值不超过m，即max{m1,m2,m3,....,mi} <= m，则称它属于n的一个m划分。这里我们记n的m划分的个数为f(n,m)；

例如当n=4时，它有5个划分：{4}、{3,1}、{2,2}、{2,1,1}、{1,1,1,1}；

注意：4=1+3和4=3+1被认为是同一个划分。

该问题是求出n的所有划分个数，即f(n,n)。下面我们考虑求f(n,m)的方法。

 

方法一：递归法

根据n和m的关系，考虑下面几种情况：

（1）当n=1时，不论m的值为多少（m>0），只有一种划分，即{1}；

（2）当m=1时，不论n的值为多少（n>0），只有一种划分，即{1,1,....1,1,1}；

（3）当n=m时，根据划分中是否包含n，可以分为两种情况：

（a）划分中包含n的情况，只有一个，即{n}；

（b）划分中不包含n的情况，这时划分中最大的数字也一定比n小，即n的所有（n-1）划分；

  因此，f(n,n) = 1 + f(n, n - 1)。

（4）当n<m时，由于划分中不可能出现负数，因此就相当于f(n,n)；

（5）当n>m时，根据划分中是否包含m，可以分为两种情况：

（a）划分中包含m的情况，即{m,{x1,x2,x3,...,xi}}，其中{x1,x2,x3,...,xi}的和为n-m，可能再次出现m，因此是（n-m）的m划分，因此这种划分个数为f(n-m, m)；

（b）划分中不包含m的情况，则划分中所有值都比m小，即n的（m-1）划分，个数为f(n, m - 1)；

 因此，f(n,m) = f(n - m,m) + f(n, m - 1)。

综合以上各种情况，可以看出，上面的结论具有递归定义的特征，其中（1）和（2）属于回归条件，（3）和（4）属于特殊情况，而情况（5）为通用情况，属于递归的方法，其本质主要是通过减少n或m以达到回归条件，从而解决问题。

其递归表达式如下所示。

参考源码1.1（递归版本（较慢））

[cpp] view plain copy

1. #include <stdio.h>  
2.   
3. #define MAXNUM 100            //最高次数  
4.   
5. //递归法求解整数划分  
6. unsigned long GetPartitionCount(int n, int max)  
7. {  
8.     if(n == 1 || max == 1)  
9.     {  
10.         return 1;  
11.     }  
12.     if(n < max)  
13.     {  
14.         return GetPartitionCount(n, n);  
15.     }  
16.     if(n == max)  
17.     {  
18.         return 1 + GetPartitionCount(n, n - 1);  
19.     }  
20.     else  
21.     {  
22.         return GetPartitionCount(n - max, max) + GetPartitionCount(n, max - 1);  
23.     }  
24. }  
25.   
26.   
27. int main(int argc, char **argv)  
28. {  
29.     int n;  
30.     int m;  
31.     unsigned long count;  
32.     while(1)  
33.     {  
34.         scanf("%d", &n);  
35.         if(n<=0)  
36.             return 0;  
37.         m=n;  
38.         count = GetPartitionCount(n, m);  
39.         printf("%d\n",count);  
40.     }  
41.     return 0;  
42. }  

方法二：动态规划

考虑到使用递归中，很多的子递归重复计算，这样不仅在时间开销特别大，这也是运算太慢的原因，比如算120的时候需要3秒中，计算130的时候需要27秒钟，在计算机200的时候....计算10分钟还没计算出来。。。鉴于此，可以使用动态规划的思想进行程序设计，原理如同上面一样，分成三种情况，只是使用一个数组来代替原有的递归，具体可以参看源码，源码中提供了两个版本 递归+记录版本和数组版本

2.1 递归加记录版本

此版本使用数组标记，如果之前计算过，则直接调用数组中内容，否则计算子递归，这样保证了每次计算一次，减少冗余量

源码如下：

[cpp] view plain copy

1. /*---------------------------------------------- 
2.  *        Author    :NEWPLAN 
3.  *        Date    :2015-04-01 
4.  *        Email    :xxxxxxx 
5.  *        Copyright:NEWPLAN 
6. -----------------------------------------------*/  
7. #include <iostream>  
8.   
9.   
10. #define MAXNUM 100            //最高次数  
11. unsigned  long ww[MAXNUM*11][MAXNUM*11];  
12. unsigned long dynamic_GetPartitionCount(int n, int max);  
13.   
14. using namespace std;  
15. int main(int argc, char **argv)  
16. {  
17.     int n;  
18.     int m;  
19.     unsigned long count;  
20.       
21.     while(1)  
22.     {  
23.         cin>>n;  
24.         cout<<dynamic_GetPartitionCount(n,n)<<endl;  
25.     }  
26.       
27.     return 0;  
28. }  
29.   
30. unsigned long dynamic_GetPartitionCount(int n, int max)  
31. {  
32.     if(n == 1 || max == 1)  
33.     {  
34.         ww[n][max]=1;  
35.         return 1;  
36.     }  
37.     if(n < max)  
38.     {  
39.         ww[n][n]=ww[n][n]? ww[n][n] : dynamic_GetPartitionCount(n, n);  
40.         return ww[n][n];  
41.     }  
42.     if(n == max)  
43.     {  
44.         ww[n][max]=ww[n][n-1]?1+ww[n][n-1]:1 + dynamic_GetPartitionCount(n, n - 1);  
45.         return ww[n][max];  
46.     }  
47.     else  
48.     {  
49.         ww[n][max]=ww[n - max][max]? (ww[n - max][max]) : dynamic_GetPartitionCount(n - max, max);  
50.         ww[n][max]+=ww[n][max-1]? (ww[n][max-1]): dynamic_GetPartitionCount(n, max - 1);      
51.         return ww[n][max];  
52.     }  
53. }  

 

2.2 数组标记法动态规划（从小到大）

考虑到计算ww[10][10]=ww[10][9]+1;所以在每次计算中都是用到之前的记录，这样就可以先从小到大计算出程序，使得计算较大数的时候调用已经计算出的较小的记录，程序直接是用循环就可以完成任务，避免了重复计算和空间栈的开销。

源码：

[cpp] view plain copy

1. /*---------------------------------------------- 
2.  *        Author    :NEWPLAN 
3.  *        Date    :2015-04-01 
4.  *        Email    :xxxxxxx 
5.  *        Copyright:NEWPLAN 
6. -----------------------------------------------*/  
7. #include <iostream>  
8.   
9. #define MAXNUM 100            //最高次数  
10.   
11. unsigned  long ww[MAXNUM*11][MAXNUM*11];  
12. unsigned long dynamic_GetPartitionCount(int n, int max);  
13.   
14. using namespace std;  
15.   
16. int main(int argc, char **argv)  
17. {  
18.     int n;  
19.     int m;  
20.     unsigned long count;  
21.       
22.     while(1)  
23.     {  
24.         cin>>n;  
25.         cout<<dynamic_GetPartitionCount(n,n)<<endl;  
26.     }  
27.       
28.     return 0;  
29. }  
30.   
31. unsigned long dynamic_GetPartitionCount(int n, int max)  
32. {  
33.     for(int i=1;i<=n;i++)  
34.         for(int j=1;j<=i;j++)  
35.         {  
36.             if(j==1|| i==1)  
37.             {  
38.                 ww[i][j]=1;  
39.             }  
40.             else   
41.             {  
42.                 if(j==i)  
43.                     ww[i][j]=ww[i][j-1]+1;  
44.                 else if((i-j)<j)  
45.                     ww[i][j]=ww[i-j][i-j]+ww[i][j-1];  
46.                 else  
47.                     ww[i][j]=ww[i-j][j]+ww[i][j-1];  
48.             }  
49.         }  
50.     return ww[n][max];  
51. }  

 

三种方法效果对比十分明显，在写此博客之前测试数据200，动态规划版本输入直接算出结果，现在这片博客写完了，，，使用递归的还没计算出结果。。。

 

 

方法三：母函数

 

    下面我们从另一个角度，即“母函数”的角度来考虑这个问题。

    所谓母函数，即为关于x的一个多项式G(x)：

    有G(x) = a0 + a1*x + a2*x^2 + a3*x^3 + ......

    则我们称G(x)为序列(a0, a1, a2,.....)的母函数。关于母函数的思路我们不做更过分析。

    我们从整数划分考虑，假设n的某个划分中，1的出现个数记为a1，2的个数记为a2，.....，i的个数记为ai，

    显然有：ak <= n/k（0<= k <=n）

    因此n的划分数f(n,n)，也就是从1到n这n个数字抽取这样的组合，每个数字理论上可以无限重复出现，即个数随意，使它们的综合为n。显然，数字i可以有如下可能，出现0次（即不出现），1次，2次，......，k次等等。把数字i用（x^i）表示，出现k次的数字i用（x^(i*k)）表示，不出现用1表示。

    例如，数字2用x^2表示，2个2用x^4表示，3个2用x^6表示，k个2用x^2k表示。

    则对于从1到N的所有可能组合结果我们可以表示为：

    G(x) = ( 1 + x + x^2 + x^3 + ... + x^n)*(1 + x^2 + x^4 + x^6 + ....)....(1 + x^n)

            = g(x,1)*g(x,2)*g(x,3)*....*g(x,n)

            = a0 + a1*x + a2*x^2 +...+ an*x^n + ....//展开式

    上面的表达式中，每个括号内的多项式代表了数字i的参与到划分中的所有可能情况。因此，该多项式展开后，由于x^a *x^b = x^(a+b)，因此x^i就代表了i的划分，展开后（x^i）项的系数也就是i的所有划分个数，即f(n,n) = an。

    由此我们找到了关于整数划分的母函数G(x)；剩下的问题就是，我们需要求出G(x)的展开后的所有系数。

    为此，我们首先要做多项式乘法，对于我们来说，并不困难。我们把一个关于x的多项式用一个整数数组a[]表示，a[i]代表x^i的系数，即：

    g(x) = a[0] + a[1]x + a[2]x^2 + ... + a[n]x^n;

    则关于多项式乘法的代码如下，其中数组a和数组b表示两个要相乘的多项式，结果存储到数组c中。

参考题目： HDU:1028：Ignatius and the Princess III

参考源码：

 

[cpp] view plain copy

1. #include <iostream>  
2. #include <string.h>  
3. #include <stdio.h>  
4.   
5. using namespace std;  
6.   
7. const int N=10005;  
8.   
9. int c1[N],c2[N];  
10.   
11. int main()  
12. {  
13.     int n,i,j,k;  
14.     while(cin>>n)  
15.     {  
16.         if(n==0) break;  
17.         for(i=0;i<=n;i++)  
18.         {  
19.             c1[i]=1;  
20.             c2[i]=0;  
21.         }  
22.         for(i=2;i<=n;i++)  
23.         {  
24.             for(j=0;j<=n;j++)  
25.                 for(k=0;k+j<=n;k+=i)  
26.                     c2[k+j]+=c1[j];  
27.             for(j=0;j<=n;j++)  
28.             {  
29.                 c1[j]=c2[j];  
30.                 c2[j]=0;  
31.             }  
32.         }  
33.         cout<<c1[n]<<endl;  
34.     }  
35.     return 0;  
36. }  

方法四：五边形数定理

 

设第n个五边形数为，那么，即序列为：1, 5, 12, 22, 35, 51, 70, ... 

对应图形如下：

设五边形数的生成函数为，那么有：

 

 

 

 

以上是五边形数的情况。下面是关于五边形数定理的内容：

 

五边形数定理是一个由欧拉发现的数学定理，描述欧拉函数展开式的特性。欧拉函数的展开式如下：

 

 

 

欧拉函数展开后，有些次方项被消去，只留下次方项为1, 2, 5, 7, 12, ...的项次，留下来的次方恰为广义五边形数。 

 

五边形数和分割函数的关系

 

欧拉函数的倒数是分割函数的母函数，亦即：

 

   其中为k的分割函数。

 

上式配合五边形数定理，有：

 

 

 

在 n>0 时，等式右侧的系数均为0，比较等式二侧的系数，可得

 

 

因此可得到分割函数p(n)的递归式：

 

例如n=10时，有：

 

 

所以，通过上面递归式，我们可以很快速地计算n的整数划分方案数p(n)了。

 

 

参考例题：

HUD4651:Partition

源码：

 

[cpp] view plain copy

1. #include <iostream>  
2.   
3. using namespace std;  
4.   
5. #define  MYDATA long long  
6. const MYDATA MOD=1000000007;  
7.   
8. #define  AMS 100005  
9. MYDATA pp[AMS];  
10. MYDATA asist[2*AMS];  
11. void myinit()  
12. {  
13.     for(int i=0;i<AMS;i++)  
14.     {  
15.         /*算出五角数（正常五角数为1,5,12,22.... k*(3*k-1)/2）*/  
16.         /*此部分，需要算出的是分割函数(1,2,5,7,12,15,22,26..... 
17.         [k*(3*k-1)/2,k*(3*k+1)/2 ])*/  
18.         asist[2*i]=i*(i*3-1)/2;  
19.         asist[2*i+1]=i*(i*3+1)/2;  
20.     }  
21. }  
22. void mymethod()  
23. {  
24.     pp[1]=1;  
25.     pp[2]=2;  
26.     pp[0]=1;  
27.     for(int i=3;i<AMS;i++)  
28.     {  
29.         int k=0;  
30.         int flags;  
31.         pp[i]=0;  
32.         /*pp[n]=pp[n-1]+pp[n-2]-pp[n-5]-pp[n-7]+pp[12]+pp[15] 
33.         -.... ..... [+pp[n-k*[3k-1]/2]  + pp[n-k*[3k+1]/2]]*/  
34.         for(int j=2;asist[j]<=i;j++)  
35.         {  
36.             /*说明：式子中+MOD是必须的，否则输出可能出错（有可能为负数）*/  
37.             flags=k&2;  
38.             if(!flags)  
39.                 pp[i]=(pp[i]+pp[i-asist[j]]+MOD)%MOD;  
40.             else  
41.                 pp[i]=(pp[i]-pp[i-asist[j]]+MOD)%MOD;  
42.             k++;  
43.             k%=8;  
44.         }  
45.     }  
46. }  
47.   
48. int main()  
49. {   
50.     int t,n;  
51.     myinit();  
52.     mymethod();  
53.     
54.     cin>>t;  
55.     while(t--)  
56.     {  
57.         cin>>n;  
58.     cout<<pp[n]<<endl;  
59.     }  
60.     return 0;  
61. }  

 

附加：

给定一个整数n，输出这个整数拆分的可能形式（即输出全部情况）

使用递归情况

整个输出类似于一颗树，以分解6为例，过程如下图

源码实现：

[cpp] view plain copy

1. #include <stdio.h>  
2.   
3. //使用一个数组记录在递归过程中产生的前面需要重复输出的值  
4. int set[100];  
5. //用于在递归过程中判断是否递归到最深处，输出回车  
6. int k;  
7.   
8. //此函数表示使用不大于m的整数对n进行拆分的情况，i用于表示set数组已经存在的记录数长度  
9. void q(int n,int m,int i)  
10. {  
11.     if(n==k&&n!=m)  
12.     {  
13.         //此时递归栈已经退回到某一分支的最上层，输出回车  
14.         //并重置计数器i为0  
15.         printf("\n");  
16.         i=0;  
17.     }  
18.     if(n==1)  
19.     {  
20.         //当n为1，意味者着只能表示1  
21.         printf("1 ");  
22.         return;  
23.     }  
24.     else if(m==1)  
25.     {  
26.         //当m为1，意味着要输出n个m相加  
27.         for(int i=0; i<n-1; i++)  
28.             printf("1+");  
29.         printf("1 ");  
30.         return;  
31.     }  
32.     if(n<m)  
33.     {  
34.         q(n,n,i);  
35.     }  
36.     if(n==m)  
37.     {  
38.         //当n等于m时，到达本次递归求和的一个叶子，此时需要输出多一个空格，表示下一次输出为另一个叶子  
39.         printf("%d ",n);  
40.         //在递归输出另一个叶子之前，将之前记录的在叶子之上的数一并输出，如上图示过程1  
41.         for(int j=0; j<i; j++)  
42.             printf("%d+",set[j]);  
43.         q(n,m-1,i);  
44.   
45.     }  
46.     if(n>m)  
47.     {  
48.         //如果n大于m，使用m作为分解，则要首先输出m+的形式  
49.         printf("%d+",m);  
50.         //记录下作为树干节点m的值并使i自增  
51.         set[i++]=m;  
52.         //递归输出m+以后的分解  
53.         q(n-m,m,i);  
54.         //递归完毕后需要将数组记录后退一个，回到上一个节点，如上图示过程2  
55.         i--;  
56.         //执行另一个分支，在下一次递归之前输出记录的数据，如上图示过程3  
57.         for(int j=0; j<i; j++)  
58.             printf("%d+",set[j]);  
59.         //递归输出另一分支情况  
60.         q(n,m-1,i);  
61.     }  
62.   
63.   
64. }  
65.   
66. int main()  
67. {  
68.     int n;  
69.     while(scanf("%d",&n)!=EOF)  
70.     {  
71.         if(n<=0)  
72.         {  
73.             printf("Please input a positive interger.\n\n");  
74.             continue;  
75.         }  
76.         k=n;  
77.         q(n,n,0);  
78.         printf("\n\n");  
79.     }  
80.     return 0;  
81. }