整理如何选取后缀数组&&后缀自动机

Posted 2020-10-17 ---学习ing---

 后缀家族已知成员

        后缀树

        后缀数组

        后缀自动机

        后缀仙人掌

        后缀预言

        后缀Splay ？

后缀树是后缀数组和后缀自动机的祖先? 功能还是比较强大的，在回文串或者字典序方面还是有用处。 而且现在已经有了线性的建树方法。

（但其实我也没用过后缀树。）下面对比后缀自动机和后缀数组

 

 

• 单个字符串问题                                                                  不等号是“优于”，&&是差不多（以下是个人感觉）

  • 1重复子串
    • 1，1 可交叉最长重复子串                              后缀自动机>=后缀数组                          都是基本题，但是前者代码稍短
    • 1，2 不可交叉最长重复子串                          后缀数组>=后缀自动机                          前者易于判断交叉；后者则需要记录每个状态所有出现的位置
    • 1，3 可交叉的k次最长重复子串                     后缀自动机>=后缀数组                          后者需+二分判定；前者无需判断，直接拓扑出每个状态的次数                     
  • 2子串个数问题
    • 2，1 不相同子串个数                                     后缀自动机&&后缀数组                          都是基本功能，易于实现。
  • 3循环子串问题
    • 3，1 求最小循环节                                         后缀数组，kmp                                           后缀自动机应该不行。
    • 3，2 重复次数最多的连续重复子串                后缀数组

• 两个字符串串问题

  • 1公共子串问题 
    • 1，1 最长公共子串                                         后缀自动机&&后缀数组                          都是基本功能
  • 2子串个数问题
    • 2，1 特定长度的公共子串                              后缀自动机&&后缀数组                           二者的基本功能

• 多个字符串问题

  • 1公共子串问题
    • 1，1 在k个字符串中的出现的最长子串           广义后缀自动机>=后缀数组（KMP也可以求多个串的最长公共字串）               （具体效率谁高取决于数据）
    • 1，2 在每个字符串中出现k次的最长子串       广义后缀自动机>=后缀数组
    • 1，3 在每个字符串中或反转后出现的最长子串 广义后缀自动机?后缀数组            

• 其他

• 最小表示法： 后缀自动机                
• 最小循环节 ：后缀数组

个人感觉：

单串和两串的题，基本上用后缀数组或者后缀自动机都可以实现。多串的题用广义后缀自动机也是非常强的，有点题如果要用后缀数组，则必须要用RMQ（树状数组||ST）+二分，甚至要用Splay来解决。当然灵活的运用后缀数组加各种工具来解决问题，才能应对各种难题，毕竟后缀自动机也是有局限的。个人更倾向于写后缀自动机，感觉好实现一点，代码也好看一点。

下面对比一下多串字符串的处理

广义后缀自动机的题：

             

POJ3294：  题意：给定一些模板字符串，求一个最长公共字串，这个最长公共字串至少在一半以上的字符串里出现过。

                    对比：如果是后缀数组，则要+二分+RMQ；而广义后缀自动机只需要记录出现的位置，最后传递即可。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<memory>
#include<cmath>
#define maxn 350003
using namespace std;
int n,len,ans,Max,now;
char s[1010],cap[1010];
struct SAM
{
    int ch[maxn][26],fa[maxn],maxlen[maxn],Last,sz;
    int root,nxt[maxn],size[maxn];
    void init()
    {
        sz=0;
        root=++sz;
        memset(size,0,sizeof(size));
        memset(ch[1],0,sizeof(ch[1]));
        memset(nxt,0,sizeof(nxt));
    }
    void add(int x)
    {
        int np=++sz,p=Last;Last=np;
        memset(ch[np],0,sizeof(ch[np]));
        maxlen[np]=maxlen[p]+1;
        while(p&&!ch[p][x]) ch[p][x]=np,p=fa[p];
        if(!p) fa[np]=1;
        else {
            int q=ch[p][x];
            if(maxlen[p]+1==maxlen[q]) fa[np]=q;
            else {
                int nq=++sz;
                memcpy(ch[nq],ch[q],sizeof(ch[q]));size[nq]=size[q]; nxt[nq]=nxt[q];
                maxlen[nq]=maxlen[p]+1;
                fa[nq]=fa[q];
                fa[q]=fa[np]=nq;
                while(p&&ch[p][x]==q) ch[p][x]=nq,p=fa[p];
            }
        }
        for(;np;np=fa[np]) 
          if(nxt[np]!=now) {
              size[np]++;
              nxt[np]=now;
          }else break;
    }
    void dfs(int x,int d){//输出    
       if(d!=maxlen[x] || d>ans) return;
       if(maxlen[x]==ans && size[x]>n){ puts(cap); return; }
          for(int i=0;i<26;++i)
          if(ch[x][i]){ cap[d]=i+\'a\'; dfs(ch[x][i],d+1); cap[d]=0; }
    }
};
SAM Sam;
int main()
{
    while(~scanf("%d",&n)&&n){     
        Sam.init();
        for(int i=1;i<=n;i++) {
            scanf("%s",s+1);
            Sam.Last=Sam.root;
            len=strlen(s+1);
            now=i;
            for(int j=1;j<=len;j++) Sam.add(s[j]-\'a\');
        }
        Max=0;ans=0;n>>=1;
        for(int i=1;i<=Sam.sz;i++) 
            if(Sam.size[i]>n&&Sam.maxlen[i]>ans) { Max=i;ans=Sam.maxlen[i];}
        if(ans) Sam.dfs(1,0);
        else puts("?");
        puts("");
    }
    return 0;
}

View Code

SPOJ8093  题意：给定一些模板串，询问每个匹配串在多少个模板串里出现过。

                    对比：同上。传递的两种方式：每加一个字符传递一次；也可以用bitset记录在哪里出现过等到加完所有字符串后再拓扑排序，然后“亦或”向上传递。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#define N 200003
using namespace std;
int ch[N][30],fa[N],l[N],n,m,len;
int r[N],v[N],cnt,np,p,nq,q,last,root,nxt[N],now,size[N];
char s[N];
void extend(int x)
{
    int c=s[x]-\'a\';
    p=last; np=++cnt; last=np; 
    l[np]=l[p]+1;
    for (;p&&!ch[p][c];p=fa[p]) ch[p][c]=np;
    if (!p) fa[np]=root;
    else {
        q=ch[p][c];
        if (l[q]==l[p]+1) fa[np]=q;
        else {
            nq=++cnt; l[nq]=l[p]+1;
            memcpy(ch[nq],ch[q],sizeof ch[nq]); size[nq]=size[q]; nxt[nq]=nxt[q];
            fa[nq]=fa[q];
            fa[q]=fa[np]=nq;
            for (;ch[p][c]==q;p=fa[p]) ch[p][c]=nq;
        }
    }
    for (;np;np=fa[np]) 
     if (nxt[np]!=now) {
         size[np]++;
         nxt[np]=now;
     }
     else break;
}
int main()
{
    scanf("%d%d",&n,&m);
    root=++cnt;
    for(int i=1;i<=n;i++) {
        scanf("%s",s+1);
        last=root;
        len=strlen(s+1);
        now=i;
        for (int j=1;j<=len;j++) 
         extend(j);
    }
    for (int i=1;i<=m;i++) {
        scanf("%s",s+1);
        len=strlen(s+1);
        p=root;
        for (int j=1;j<=len;j++)  p=ch[p][s[j]-\'a\'];
        printf("%d\\n",size[p]);
    }
}

View Code

 (对于后缀数组，在下还不是很敏感，多做点之后再补充一些上来)

 

 顺便发两张后缀自动机的图

 

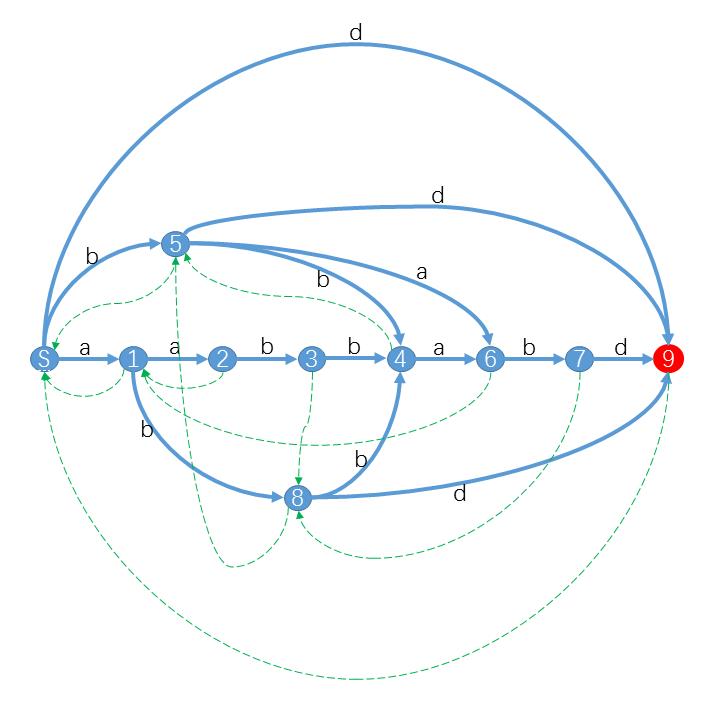
状态	子串	endpos
S	空串	{0,1,2,3,4,5,6}
1	a	{1,2,5}
2	aa	{2}
3	aab	{3}
4	aabb,abb,bb	{4}
5	b	{3,4,6}
6	aabba,abba,bba,ba	{5}
7	aabbab,abbab,bbab,bab	{6}
8	ab	{3,6}
9	aabbabd,abbabd,bbabd,babd,abd,bd,d	{7}