HDU_oj_2046 骨牌铺方格

Posted 2020-10-17 T丶jl

Problem Description

 

在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数.
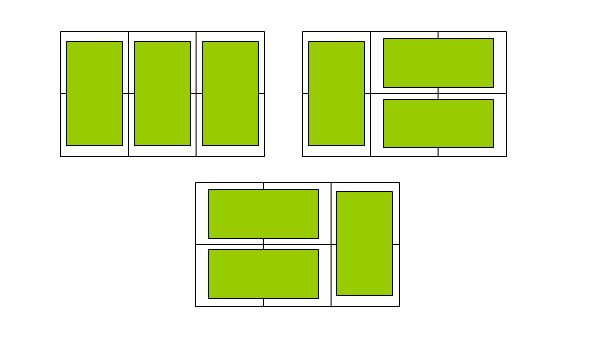
例如n=3时,为2× 3方格，骨牌的铺放方案有三种,如下图：

 

Input

输入数据由多行组成，每行包含一个整数n,表示该测试实例的长方形方格的规格是2×n (0<n<=50)。

 

Output

对于每个测试实例，请输出铺放方案的总数，每个实例的输出占一行。

 

Sample Input

1

3

2

 

Sample Output

1

3

2

 

分析：

又是典型的递归问题

第n个规格的种数取决于第n-1个的规格和第n-2个的规格

两种情况

①第n个规格的前一个如果是竖放，则这种情况有F(n-1)种

②第n个规格是两个横放的，则这种情况有F(n-2)种

所以，F(n)=F(n-1)+F(n-2)

注意点：

 

 1 //递归解法，但不是递归写法
 2 #include<iostream>
 3 using namespace std;
 4 
 5 int main()
 6 {
 7     int n;
 8     long long fx,fy,fz;
 9     while(cin>>n)
10     {
11         fx=1;fy=2;
12         if(n==1)
13         cout<<fx<<endl;
14         else if(n==2)
15         cout<<fy<<endl;
16         else
17         {
18             n-=2;
19             while(n--)
20             {
21                 fz=fy+fx;
22                 fx=fy;
23                 fy=fz;
24             }
25             cout<<fz<<endl;
26         }
27     }
28 }