这次还是能看的0 0，没出现一题掉分情况。
QAQ前两次掉分还被hack了0 0,两行清泪。
A. Find Extra One
You have n distinct points on a plane, none of them lie on OY axis. Check that there is a point after removal of which the remaining points are located on one side of the OY axis.
The first line contains a single positive integer n (2?≤?n?≤?105).
The following n lines contain coordinates of the points. The i-th of these lines contains two single integers xi and yi (|xi|,?|yi|?≤?109,xi?≠?0). No two points coincide.
Print "Yes" if there is such a point, "No" — otherwise.
You can print every letter in any case (upper or lower).
3
1 1
-1 -1
2 -1
Yes
4
1 1
2 2
-1 1
-2 2
No
3
1 2
2 1
4 60
Yes
题意：给你n个平面上的点，能否去掉一个使得所有点在y轴一侧。给出的点不会在y轴上。
题解：水题，统计下x>0 和 x<0的数字个数就好了。
1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define mod 1000000007 5 #define LL long long 6 #define INF 0x3f3f3f3f 7 using namespace std; 8 int main() 9 { 10 int n,left,right,x,y; 11 left=right=0; 12 scanf("%d",&n); 13 for(int i=1;i<=n;i++) 14 { 15 scanf("%d%d",&x,&y); 16 if(x>0) 17 right++; 18 else 19 left++; 20 } 21 if(right<=1 || left<=1) 22 printf("Yes\n"); 23 else 24 printf("No\n"); 25 return 0; 26 }
B. Position in Fraction
You have a fraction 
. You need to find the first occurrence of digit c into decimal notation of the fraction after decimal point.
The first contains three single positive integers a, b, c (1?≤?a?<?b?≤?105, 0?≤?c?≤?9).
Print position of the first occurrence of digit c into the fraction. Positions are numbered from 1 after decimal point. It there is no such position, print -1.
1 2 0
2
2 3 7
-1
题意：给出一个分数$ \frac{a}{b} $ ，看c在该分数小数点后几位。
题解：$ \frac{a}{b} $化为最简$ \frac{a‘}{b‘} $后，我们模拟除法列竖式求答案的过程。由于列竖式的过程中余下的数总比b‘小，所以最多b‘个不同余数，列竖式的过程中一旦出现相同的余数则是进入了循环。所以我们最多做b‘次除法就能求出c是否存在于该分数小数点后以及c的位置。
1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define mod 1000000007 5 #define LL long long 6 #define INF 0x3f3f3f3f 7 using namespace std; 8 int gcd(int a,int b) 9 { 10 int c; 11 while(b) 12 { 13 c=a%b; 14 a=b; 15 b=c; 16 } 17 return a; 18 } 19 int main() 20 { 21 int a,b,c,d,e,i; 22 scanf("%d%d%d",&a,&b,&c); 23 d=gcd(a,b); 24 a/=d; 25 b/=d; 26 d=a/b; 27 a-=d*b; 28 a*=10; 29 for(i=1;i<=100000;i++) 30 { 31 d=a/b; 32 a-=d*b; 33 if(d==c) 34 break; 35 a*=10; 36 } 37 if(i>100000) 38 printf("-1\n"); 39 else 40 printf("%d\n",i); 41 return 0; 42 }
C. Remove Extra One
You are given a permutation p of length n. Remove one element from permutation to make the number of records the maximum possible.
We remind that in a sequence of numbers a1,?a2,?...,?ak the element ai is a record if for every integer j (1?≤?j?<?i) the following holds:aj?<?ai.
The first line contains the only integer n (1?≤?n?≤?105) — the length of the permutation.
The second line contains n integers p1,?p2,?...,?pn (1?≤?pi?≤?n) — the permutation. All the integers are distinct.
Print the only integer — the element that should be removed to make the number of records the maximum possible. If there are multiple such elements, print the smallest one.
1
1
1
5
5 1 2 3 4
5
In the first example the only element can be removed.
题意:给出1~n的一个排列，要求你找出一个数，在排列中去掉它以后符合条件的数最多，如果有多个则选最小的那个。若ai符合条件，对于任意1≤j<i，aj<ai。
题解：那么我们写个bit来记录数列前面小于ai的个数，set来求取大于ai的第一个数。如果ai前面有i-2个数小于ai，那么用set的lonwer_bound找到大于ai的第一个数p，并且该数p对于答案的贡献num[p]++。注意如果ai前面有i-1个数小于ai，那么ai对于答案的贡献num[ai]--。然后从小到大找贡献最大的那个。
1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define mod 1000000007 5 #define LL long long 6 #define INF 0x3f3f3f3f 7 using namespace std; 8 const int N=1e5+10; 9 int bits[N]; 10 int num[N]; 11 int n,m,T,k,p; 12 set<int> pt; 13 set<int>::iterator it; 14 void add(int i,int x) 15 { 16 while(i<=n) 17 { 18 bits[i]+=x; 19 i+=(i &(-i)); 20 } 21 return ; 22 } 23 int sum(int i) 24 { 25 int res=0; 26 while(i>0) 27 { 28 res+=bits[i]; 29 i-=(i &(-i)); 30 } 31 return res; 32 } 33 int main() 34 { 35 scanf("%d",&n); 36 for(int i=1;i<=n;i++) 37 { 38 scanf("%d",&p); 39 if((p-1>0 && sum(p-1)==i-2) || (p-1==0 && i==2)) 40 { 41 it=pt.lower_bound(p); 42 num[*it]++; 43 } 44 if((p-1>0 && sum(p-1)==i-1) || (p-1==0 && i==1)) 45 num[p]--; 46 pt.insert(p); 47 add(p,1); 48 } 49 int maxn=num[1]; 50 k=1; 51 for(int i=2;i<=n;i++) 52 { 53 if(maxn<num[i]) 54 { 55 maxn=num[i]; 56 k=i; 57 } 58 } 59 printf("%d\n",k); 60 return 0; 61 }
D. Unusual Sequences
Count the number of distinct sequences a1,?a2,?...,?an (1?≤?ai) consisting of positive integers such that gcd(a1,?a2,?...,?an)?=?x and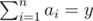 
. As this number could be large, print the answer modulo 109?+?7.
gcd here means the greatest common divisor.
The only line contains two positive integers x and y (1?≤?x,?y?≤?109).
Print the number of such sequences modulo 109?+?7.
3 9
3
5 8
0
题意：让你找出符合条件的序列数，并mod 1e9+7。序列需满足gcd（a1~n）=x,sum(a1~n）=y。
题解：首先把一个数p分解成几个数成组成的序列有$ 2^{p-1} $，用组合的隔板法轻易可证。x能整除y说明存在这样的序列，反之不存在。然后d=y/x，将d分解成质数乘积，算算不同质数的个数以及具体是哪些质数，容斥一下就能求出答案了。
1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define mod 1000000007 5 #define LL long long 6 #define INF 0x3f3f3f3f 7 using namespace std; 8 const int N=1e5+10; 9 int prime[N],inf[N],pcnt; 10 void primer(int n) 11 { 12 pcnt=0; 13 for(int i=2;i<=n;i++) 14 { 15 if(!inf[i]) 16 { 17 prime[++pcnt]=i; 18 } 19 for(int j=1;j<=pcnt;j++) 20 { 21 if(prime[j]>n/i) break; 22 inf[prime[j]*i]=1; 23 if(i%prime[j]==0) break; 24 } 25 } 26 return ; 27 } 28 LL quick_pow(LL x,LL n) 29 { 30 LL res=1; 31 while(n) 32 { 33 if(n&1) 34 res=(res*x)%mod; 35 n>>=1; 36 x=(x*x)%mod; 37 } 38 return res; 39 } 40 LL x,y,d,n,k; 41 int all; 42 LL num[20]; 43 int cnt; 44 LL ans,p; 45 int main() 46 { 47 primer(100000); 48 scanf("%lld%lld",&x,&y); 49 if(y%x!=0) 50 { 51 printf("0\n"); 52 return 0; 53 } 54 y/=x; 55 d=y; 56 cnt=0; 57 for(int i=1;(LL)prime[i]*prime[i]<=d;i++) 58 { 59 n=(LL)prime[i]; 60 if(d%n==0) 61 { 62 num[++cnt]=n; 63 while(d%n==0) d/=n; 64 } 65 } 66 if(d!=1) num[++cnt]=d; 67 ans=0; 68 all=(1<<cnt)-1; 69 for(int i=0,j,k,ok;i<=all;i++) 70 { 71 j=i; 72 k=0; 73 p=1; 74 ok=1; 75 while(j) 76 { 77 k++; 78 if(j&1) p*=num[k],ok=-ok; 79 j>>=1; 80 } 81 ans=(ans+quick_pow(2,y/p-1)*ok)%mod; 82 } 83 printf("%lld\n",(ans%mod+mod)%mod); 84 return 0; 85 }