求图中欧拉回路数量

Posted 2020-10-17 Zinn

问题描述：输入点数n、边数m、每条边连接的两个点a,b，求此无向图中不包括一个点本身的欧拉回路数量，重复不计；

解决此问题，则需要在深搜的基础上判断新搜出的欧拉回路是否已经被走过，可以利用搜索时所打的标记来判断；

使用邻接表，需要注意在无向图中连接两点有两条边，要同时考虑；

以下为代码：

---

 

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int n,m,cnt[105],ct,qd,t,ld[205];
bool b[205],lu[105][205],qdf=0;
struct N{
　　int hd;int to;int next;
}edge[205];
void add(int x,int y)
{
　　ct++;
　　edge[ct].to=y;
　　edge[ct].hd=x;
　　edge[ct].next=cnt[x];
　　cnt[x]=ct;
}
void pd()
{
　　t++;
　　memcpy(lu[t],b,sizeof lu[t]);
　　for(int i=1;i<t;i++)
　　{
　　　　bool fl=0;
　　　　for(int j=1;j<=m*2;j++)
　　　　if(lu[i][j]!=lu[t][j])fl=1;
　　　　if(!fl)//若完全相同,撤销该路 
　　　　{
　　　　　　memset(lu[t],0,sizeof lu[t]);
　　　　　　t--;
　　　　　　break;
　　　　} 
　　}
}
void dfs(int k)
{
　　if(k==qd&&!qdf)
　　{
　　　　pd();return;
　　}
　　qdf=0;
　　for(int i=cnt[k];i>0;i=edge[i].next)
　　{
　　　　if(b[i])continue;//边 
　　　　b[i]=1;b[ld[i]]=1;
　　　　dfs(edge[i].to);
　　　　b[i]=0;b[ld[i]]=0;
　　}
}
int main()
{
　　scanf("%d%d",&n,&m);
　　for(int i=1;i<=m;i++)
　　{
　　　　int a,b;
　　　　scanf("%d%d",&a,&b);
　　　　add(a,b);
　　　　ld[ct]=ct+1;
　　　　add(b,a);
　　　　ld[ct]=ct-1;
　　}
　　for(int i=1;i<=n;i++)
　　{
　　　　memset(b,0,sizeof b);
　　　　qd=i;qdf=1;
　　　　dfs(i);
　　}
　　printf("%d",t);
　　return 0;
}

---

 

样例

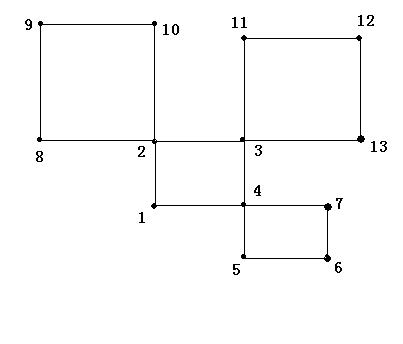
输入

13 16
1 2
2 3
3 4
4 1
2 8
8 9
9 10
10 2
3 11
11 12
12 13
13 3
4 7
7 6
6 5
5 4

输出

11