模板点分治
Posted YXY_1211
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了模板点分治相关的知识,希望对你有一定的参考价值。
最近被迫学习了点分治。
点分治一般用来解决这样一类问题:给出一棵树,求出这棵树上任意两个点之间距离小于等于k的点对个数。
难点在于,两个顶点之间可能会跨过根。普通的算法可能时间复杂度会很高,所以这里介绍点分治算法。
- 首先,我们有一棵树(需要根据题目情景建立,多用邻接表)↓

由于在树上求解是通过递归实现的,因此为了最大限度的简化时间复杂度,我们应该找到一种树的排列方式,使递归层数最少(也就是树的深度最小)。
这里介绍一个新的概念:树的重心。找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心。删去重心后,生成的多棵树尽可能平衡。
上图的重心就是点2,当把点2作为根节点后,整棵树变形如下:
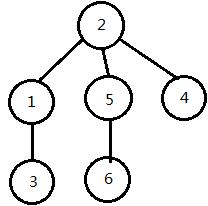 可以发现,树的深度由4变为2。
可以发现,树的深度由4变为2。
这部分的代码实现如下:
1 void get_root(int x,int fa) 2 { 3 f[x]=0,son[x]=1; //f数组记录以x为根最大子树的大小 4 for(int i=first[x];i;i=next[i]) 5 if(to[i]!=fa && !vis[to[i]]) //不用考虑根节点以及没有访问过 6 { 7 get_root(to[i],x); 8 son[x]+=son[to[i]]; //计算x结点大小 9 f[x]=max(f[x],son[to[i]]); //找到最大子树 10 } 11 f[x]=max(f[x],sn-son[x]); 12 if(f[root]>f[x]) root=x; //更新当前根 13 }
接下来开始求解。对于一棵连通树,两个顶点之间的路径只有两种情况:经过根节点和不经过根节点
不经过根节点的情况即两个点在同一棵子树上,可以通过递归求得。所以我们只需要考虑第一种情况。
这就用简单dfs就可以了,只不过要把过程中所有经过的节点距离都记录下来(顺便说一句,这里就体现出前面费点功夫找重心的好处了,递归层数少)。
下面是一道裸题:poj1741 tree
| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 25457 | Accepted: 8469 |
Description
Define dist(u,v)=The min distance between node u and v.
Give an integer k,for every pair (u,v) of vertices is called valid if and only if dist(u,v) not exceed k.
Write a program that will count how many pairs which are valid for a given tree.
Input
The last test case is followed by two zeros.
Output
Sample Input
5 4 1 2 3 1 3 1 1 4 2 3 5 1 0 0
Sample Output
8
Source
如果deep[i]+deep[j]≤m,则点对(i,t)(i<t≤j)都符合题意,将j-i加入答案中,并且i++;否则j--。
然而这样还会重复计算在同一棵子树中的点对,所以在进行下一步dfs之前需要减去重复部分。(也就是无向图中会出现这种情况)

1 #include <iostream> 2 #include <cmath> 3 #include <cstring> 4 #include <cstdio> 5 #include <cstdlib> 6 #include <algorithm> 7 #define MAXN 10010 8 using namespace std; 9 long long m,ans; 10 int cnt,root,sn,tot; 11 int first[MAXN],to[20010],len[20010],next[20010],son[MAXN],deep[MAXN],vis[MAXN],f[MAXN],d[MAXN]; 12 void add(int x,int y,int z) //建立邻接表 13 { 14 to[++cnt]=y;len[cnt]=z; 15 next[cnt]=first[x]; //next数组记录当前起始点的前一条边的编号 16 first[x]=cnt; //first最终记录的是当前点作为起始点的最后一条边,之后从后往前遍历 17 } 18 void get_root(int x,int fa) //找重心 19 { 20 f[x]=0,son[x]=1; //f数组记录以x为根最大子树的大小 21 for(int i=first[x];i;i=next[i]) 22 if(to[i]!=fa && !vis[to[i]]) //不用考虑根节点以及没有访问过 23 { 24 get_root(to[i],x); 25 son[x]+=son[to[i]]; //计算x结点大小 26 f[x]=max(f[x],son[to[i]]); //找到最大子树 27 } 28 f[x]=max(f[x],sn-son[x]); 29 if(f[root]>f[x]) root=x; //更新当前根 30 } 31 void get_deep(int x,int fa) //求当前x为根节点的树的深度 32 { 33 d[++tot]=deep[x]; //每两个点之间的距离值都要记录 34 for(int i=first[x];i;i=next[i]) 35 if(to[i]!=fa && !vis[to[i]]) 36 { 37 deep[to[i]]=deep[x]+len[i]; 38 get_deep(to[i],x); 39 } 40 } 41 int calc(int x) 42 { 43 tot=0; 44 get_deep(x,0); 45 sort(d+1,d+tot+1); 46 int i=1,j=tot,sum=0; 47 while(i<j) //计算个数 48 { 49 if(d[i]+d[j]<=m){sum+=j-i,i++;} 50 else j--; 51 } 52 return sum; 53 } 54 void dfs(int x) 55 { 56 deep[x]=0; 57 vis[x]=1; 58 ans+=calc(x); 59 for(int i=first[x];i;i=next[i]) 60 if(!vis[to[i]]) 61 { 62 deep[to[i]]=len[i]; 63 ans-=calc(to[i]); //计算不符合题意的答案 64 sn=son[to[i]]; 65 root=0; 66 get_root(to[i],0); 67 dfs(root); 68 } 69 } 70 int main() 71 { 72 int n,x,y,z; 73 while(scanf("%d%lld",&n,&m)) 74 { 75 if(n==0 && m==0) break; 76 memset(first,0,sizeof(first)); 77 memset(vis,0,sizeof(vis)); 78 cnt=0,ans=0; 79 for(int i=1;i<n;i++) 80 { 81 scanf("%d%d%d",&x,&y,&z); 82 add(x,y,z); //无向图,建两次 83 add(y,x,z); 84 } 85 f[0]=0x7fffffff;sn=n; 86 root=0;get_root(1,0);dfs(root); 87 printf("%lld\\n",ans); 88 } 89 return 0; 90 }
以上是关于模板点分治的主要内容,如果未能解决你的问题,请参考以下文章
