[算法]浮点数在内存中的存储方式

Posted 2020-10-16 yiyide266

float型变量占用32bit，即4个byte的内存空间

我们先来看下浮点数二进制表达的三个组成部分。

三个主要成分是：

• Sign（1bit）：表示浮点数是正数还是负数。0表示正数，1表示负数
• Exponent（8bits）：指数部分。类似于科学技术法中的M*10^N中的N，只不过这里是以2为底数而不是10。需要注意的是，这部分中是以2^7-1即127，也即01111111代表2^0，转换时需要根据127作偏移调整。
  *10000000代表2^1，10000001代表2^2...实际上就是Exponent - 127 = log₂ (2^n).
  *回忆科学记数法，nE0等于其本身，即不进/退小数位，nEx则进/退x位.
• Mantissa（23bits）：基数部分。浮点数具体数值的实际表示。

下面我们来看个实际例子来解释下转换过程。
Step 1 改写整数部分
以数值5.2为例。先不考虑指数部分，我们先单纯的将十进制数改写成二进制。
整数部分很简单，5.即101.。

Step 2 改写小数部分
小数部分我们相当于拆成是2^-1一直到2^-N的和。例如：
0.2 = 0.125+0.0625+0.007825+0.00390625即2^-3+2^-4+2^-7+2^-8….，也即.00110011001100110011。

或者换个更傻瓜的方式去解读十进制对二进制小数的改写转换，通常十进制的0.5也（也就是分数1/2），相当于二进制的0.1（同等于分数1/2），

我们可以把十进制的小数部分乘以2，取整数部分作为二进制的一位，剩余小数继续乘以2，直至不存在剩余小数为止。

例如0.2可以转换为：

0.2 x 2 = 0.4     0

0.4 x 2 = 0.8     0

0.8 x 2 = 1.6     1

0.6 x 2 = 1.2     1

0.2 x 2 = 0.4     0

0.4 x 2 = 0.8     0

0.8 x 2 = 1.6     1

.......

即：.0011001.......（它是一个无限循环的二进制数，明白为什么十进制小数转换成二进制小数的时候为什么会出现精度损失的情况了吗）

Step 3 规格化
现在我们已经有了这么一串二进制101.00110011001100110011。然后我们要将它规格化，也叫Normalize。其实原理很简单就是保证小数点前只有一个bit。于是我们就得到了以下表示：1.0100110011001100110011 * 2^2。到此为止我们已经把改写工作完成，接下来就是要把bit填充到三个组成部分中去了。

Step 4 填充
指数部分（Exponent）：之前说过需要以127作为偏移量调整。因此2的2次方，指数部分偏移成2+127即129，表示成10000001填入。
整数部分（Mantissa）：除了简单的填入外，需要特别解释的地方是1.010011中的整数部分1在填充时被舍去了。因为规格化后的数值整部部分总是为1。那大家可能有疑问了，省略整数部分后岂不是1.010011和0.010011就混淆了么？其实并不会，如果你仔细看下后者：会发现他并不是一个规格化的二进制，可以改写成1.0011 * 2^-2。所以省略小数点前的一个bit不会造成任何两个浮点数的混淆。
具体填充后的结果见下图

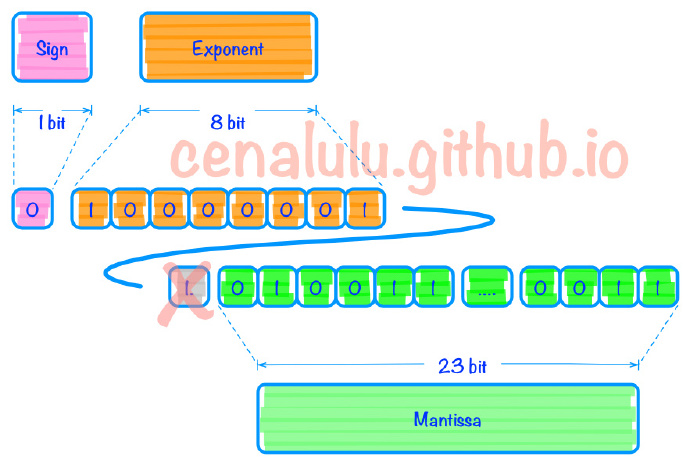
练习：如果想考验自己是否充分理解这节内容的话，可以随便写一个浮点数尝试转换。通过 浮点二进制转换工具可以验证答案。