HDU4456-Crowd （坐标旋转处理+hash处理+二维树状数组）

Posted 2020-10-16 ---学习ing---

题意：

给出一个矩阵，初始每个位置上的值都为0，然后有两种操作

•    一种是更改某个位置上的值
•   另一种是求某个位置附近曼哈顿距离不大于K的所有位置的值的总和

 技巧：

• 坐标旋转，使得操作之后菱形变成方方正正的矩形，（即“曼哈顿距离”转化为“切比雪夫距离”）方便使用树状数组进行计算。

• 利用哈希进行离散，节约空间，即不开不必要的空间。

坐标旋转：

• X=x-y
• Y=x+y

   

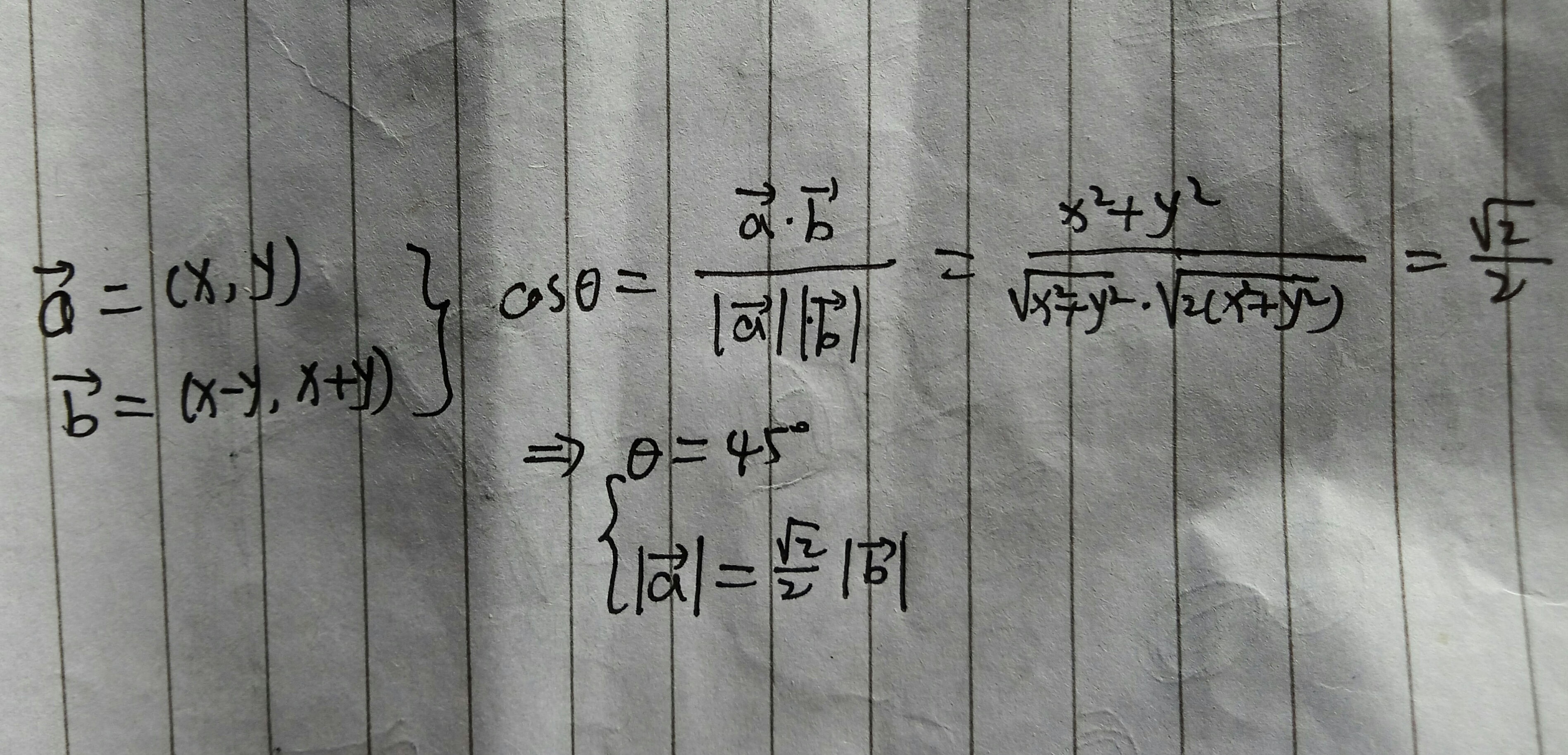
这个结果显示，A’B’C’D’（X，Y）是ABCD（x，y）绕原点（0，0）左旋转45°后的结果，同时长度变为原来的sqrt(2)倍。

由于菱形范围为对角线OA的距离，正方形为一半边长OM的距离，相等，所以无需对距离进行操作。

缩小范围：

小于0和大于2*n的一定无值。

坐标离散： 

1,离线离散

之前学主席树的时候经常这样搞。http://www.cnblogs.com/hua-dong/p/7931778.html

 

#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn=4100000;
const int maxm=100010;
int q[maxm],a[maxm],b[maxm],c[maxm];
int hs[maxn],sz,Lim,n;
int Val[maxn];
int max(int x,int y){ if(x>y) return x;return y;}
int min(int x,int y){ if(x<y) return x;return y;}
int lowbit(int x)  { return  x&(-x); }
void addhs(int x,int y)
{
    for(int i=x;i<=Lim;i+=lowbit(i))
        for(int j=y;j<=Lim;j+=lowbit(j)) {  
            hs[++sz]=i*Lim+j ;
        }  
}
void add(int x,int y,int val)
{
    for(int i=x;i<=Lim;i+=lowbit(i))
        for(int j=y;j<=Lim;j+=lowbit(j)){
           int pos=lower_bound(hs+1,hs+sz+1,i*Lim+j)-hs;
               Val[pos]+=val;
        }
}
int getsum(int x,int y)
{
    int res=0;
    for(int i=x;i;i-=lowbit(i))
        for(int j=y;j;j-=lowbit(j)){
           int pos=lower_bound(hs+1,hs+sz+1,i*Lim+j)-hs;
           if(hs[pos]==i*Lim+j)   res+=Val[pos];
        }
    return res;
}
int main()
{
    int i,m;
    while(~scanf("%d",&n)){
        if(n==0) return 0;
        sz=0;Lim=n<<1;
        memset(Val,0,sizeof(Val));
        scanf("%d",&m);
        for(i=1;i<=m;i++){
            scanf("%d%d%d%d",&q[i],&a[i],&b[i],&c[i]);
            if(q[i]==1)  addhs(a[i]-b[i]+n,a[i]+b[i]);
        }
        sort(hs+1,hs+sz+1);
        sz=unique(hs+1,hs+sz+1)-(hs+1);
        for(i=1;i<=m;i++)
        {
            if(q[i]==1){
                add(a[i]-b[i]+n,a[i]+b[i],c[i]);
            }
            else {
                int X1=max(1,a[i]-b[i]+n-c[i]);
                int Y1=max(1,a[i]+b[i]-c[i]);
                int X2=min(Lim,a[i]-b[i]+n+c[i]);
                int Y2=min(Lim,a[i]+b[i]+c[i]);
                printf("%d\\n",getsum(X2,Y2)-getsum(X1-1,Y2)+getsum(X1-1,Y1-1)-getsum(X2,Y1-1));
            }
        }
    }
    return 0;
}

 

2，线性探测再散列。

以前再kbrdhash时用到过，大同小异吧http://www.cnblogs.com/hua-dong/p/7714475.html。

 但是这种解法能否AC，完全看Mod是否取到合适的值。（我换了好多个才AC了，心累）。

#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn=41000;
const int Mod=2501003;
int Laxt[Mod],Next[Mod],H[Mod],cnt;
int q,a,b,c;
int Val[Mod],Lim,n;
int max(int x,int y){ if(x>y) return x;return y;}
int min(int x,int y){ if(x<y) return x;return y;}
int lowbit(int x)  { return  x&(-x); }
int find(int x,int opt)
{
    int tmp=x%Mod;
    for(int i=Laxt[tmp];i;i=Next[i]){
           if(H[i]==x) return i;
    }
    if(opt==0) return x=0;
    Next[++cnt]=Laxt[tmp];
    Laxt[tmp]=cnt;
    H[cnt]=x;
    return cnt;
}
void add(int x,int y,int val)
{
    for(int i=x;i<=Lim;i+=lowbit(i))
        for(int j=y;j<=Lim;j+=lowbit(j)){
           int pos=find(i*Lim+j,1);
               Val[pos]+=val;
        }
}
int getsum(int x,int y)
{
    int res=0;
    for(int i=x;i;i-=lowbit(i))
        for(int j=y;j;j-=lowbit(j)){
           int pos=find(i*Lim+j,0);
           if(H[pos]==i*Lim+j)  res+=Val[pos];
        }
    return res;
}
int main()
{
    int i,m;
    while(~scanf("%d",&n)){
        if(n==0) return 0;
        cnt=0;Lim=n<<1;
        memset(Val,0,sizeof(Val));
        memset(Laxt,0,sizeof(Laxt));
        scanf("%d",&m);
        for(i=1;i<=m;i++)
        {
            scanf("%d%d%d%d",&q,&a,&b,&c);
            if(q==1) add(a-b+n,a+b,c);
            else {
                int X1=max(1,a-b+n-c);
                int Y1=max(1,a+b-c);
                int X2=min(Lim,a-b+n+c);
                int Y2=min(Lim,a+b+c);
                printf("%d\\n",getsum(X2,Y2)-getsum(X1-1,Y2)+getsum(X1-1,Y1-1)-getsum(X2,Y1-1));
            }
        }
    }
    return 0;
}

 

经验：

为什么不把查询用到的点也离散呢？后面getsum的那些点不是到用到吗-----就算用到他们的值也为0。

算是加深对数状数组的存储位置一个更好的理解吧。

（类似用到了坐标转化的题：HDU4312）