排序算法

Posted 2020-10-16 Geek

插入排序

 

①：直接插入排序：

简单插入排序就是每一步都将一个待排数据按其大小插入到已经排序的数据中的适当位置，直到全部插入完毕。

 简单插入排序就是每一步都将一个待排数据按其大小插入到已经排序的数据中的适当位置，直到全部插入完毕。
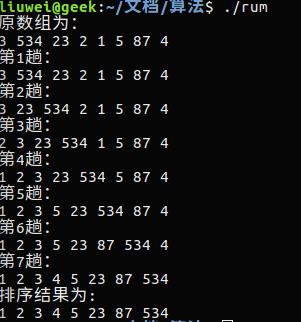
#include<stdio.h>
void print(int * a){for(int i = 0 ;i<8;printf("%d ",a[i++]));printf("\\n");}  //打印函数
void insert_sort(int* a,int len)
{
  
     int i,j,tmp;  
    for (i = 1; i < len; i++) {  
        tmp = a[i];  
          for(j = i -1;j>=0 && a[j]>tmp;j--)
          {
             a[j+1] =a[j]; 
          }
        a[j+1] = tmp;  
        printf("第%d趟：\\n",i);
        print(a);
    }   
}

void main()
{
   int b[] = {3,534,23,2,1,5,87,4};
   printf("原数组为：\\n");
   print(b);
   insert_sort(b,8); 
  
   printf("排序结果为:\\n");
   print(b); 
}

运行结果为：

②：二分插入排序：

   快速找到插入时的位置

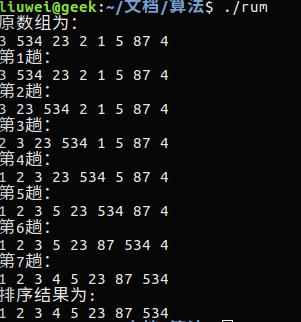
#include<stdio.h>
void print(int * a){for(int i = 0 ;i<8;printf("%d ",a[i++]));printf("\\n");}
   void  InsertSortByBinarySearch(int* arr ,int len) {
    for (int i = 1; i < len; i++) {
        int temp = arr[i];
        int low = 0, high = i - 1;
        int mid = -1;
        while (low <= high) {            
            mid = low + (high - low) / 2;            
            if (arr[mid] > temp) {               
                high = mid - 1;            
            } else {           
                low = mid + 1;            
            }        
        }        
        for(int j = i - 1; j >= low; j--) {            
            arr[j + 1] = arr[j];        
        }        
        arr[low] = temp;    
        printf("第%d趟：\\n",i);
        print(arr);
    }
}

void main()
{
   int b[] = {3,534,23,2,1,5,87,4};
   printf("原数组为：\\n");
   print(b);
   InsertSortByBinarySearch(b,8); 
  
   printf("排序结果为:\\n");
   print(b); 
}

结果为：

 

冒泡排序：

冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。

#include<stdio.h>
void print(int * a){for(int i = 0 ;i<8;printf("%d ",a[i++]));printf("\\n");}
void sort(int * a,int n)
{
  int temp;
  for(int i = 0; i < n;i++)
  {
    for(int j = 0;j<n-i;j++)
    {
     if(a[j]>a[j+1])
       {
          temp = a[j];
          a[j]=a[j+1];
          a[j+1]=temp;
       }
    }
     printf("第%d趟：\\n",i+1);
        print(a);
  }
}
void main()
{
  int b[] = {3,534,23,2,1,5,87,4};
   printf("原数组为：\\n");
   print(b);
   sort(b,8); 
  
   printf("排序结果为:\\n");
   print(b); 
}

 

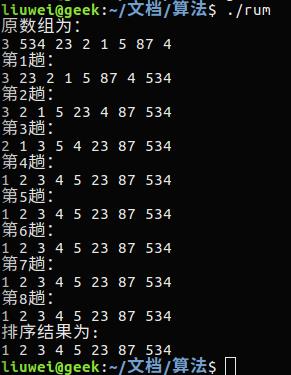
快速排序：

快速排序的基本思想：

         通过一趟排序将待排序记录分割成独立的两部分，其中一部分记录的关键字均比另一部分关键字小，则分别对这两部分继续进行排序，直到整个序列有序。

  #include<stdio.h> 
void print(int * a){for(int i = 0 ;i<8;printf("%d ",a[i++]));printf("\\n");}
void quickSort(int a[],int,int);  
int count = 1;
void main()  
{  
  int b[] = {3,534,23,2,1,5,87,4};
   printf("原数组为：\\n");
   print(b);
   quickSort(b,0,7);  
   printf("排序结果为:\\n");
   print(b); 
}  
  
void quickSort(int s[], int l, int r)  
{  
 if (l< r)  
 {
  int i = l, j = r, x = s[l];  
    while (i < j)  
    {  
        while(i < j && s[j]>= x) // 从右向左找第一个小于x的数  
         j--;   
          if(i < j)    s[i++] = s[j];  
      while(i < j && s[i]< x) // 从左向右找第一个大于等于x的数  
        i++;   
         if(i < j)    s[j--] = s[i];  
   }  
  s[i] = x;  
  quickSort(s, l, i - 1); // 递归调用  
  quickSort(s, i + 1, r);   
  
 }  
}  

选择排序：

1、基本思想：在要排序的一组数中，选出最小的一个数与第一个位置的数交换；然后在剩下的数当中再找最小的与第二个位置的数交换，如此循环到倒数第二个数和最后一个数比较为止。

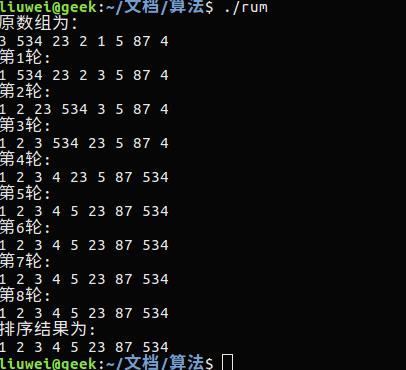
#include<stdio.h> 
void print(int * a){for(int i = 0 ;i<8;printf("%d ",a[i++]));printf("\\n");}
void selectSort(int* a,int size);  
 
void main()  
{  
  int b[] = {3,534,23,2,1,5,87,4};
   printf("原数组为：\\n");
   print(b);
   selectSort(b,8);  
   printf("排序结果为:\\n");
   print(b); 
}  
  
void selectSort(int* a,int size)
{
    
    int temp = 0 ;  
    for(int i = 0 ; i < size ; i++)
    {
        int k = i;    
        for(int j = size -1 ; j > i ; j--)
        {
                if(a[j] < a[k])
                {
                    k = j;
                }
        }
        //交换两个数
        temp = a[i];
        a[i] = a[k];
        a[k] = temp;
        printf("第%d轮:\\n",i+1);
        print(a);
    }
}

排序结果为:

希尔排序

1、基本思想：

先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行依次直接插入排序。

#include<stdio.h> 
void print(int * a){for(int i = 0 ;i<8;printf("%d ",a[i++]));printf("\\n");}
void shellSort(int* data,int size) 
    {
        int j = 0;
        int temp = 0;
        //每次将步长缩短为原来的一半
        for (int x = size / 2; x > 0; x /= 2)
        {
        for (int i = x; i < size; i++) 
        {
            temp = data[i];
            for (j = i; j >= x; j -= x) 
            {
            if(temp < data[j - x])//如想从小到大排只需修改这里
            {   
                data[j] = data[j - x];
            }
            else
            {
                break;
            }
            
            } 
            data[j] = temp;
        }
    
        }
    }
void main()
{
   int b[] = {3,534,23,2,1,5,87,4};
   printf("原数组为：\\n");
   print(b);
   shellSort(b,8); 
  
   printf("排序结果为:\\n");
   print(b); 
}

排序结果：

归并排序

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

package com.geek.algorithm;

import java.util.Random;

public class MergeSort extends BaseSort {

    public MergeSort(int[] values) {
        super(values);
    }

    @Override
    public void ascSort() {
        sort(values, 0, length - 1);
    }

    public void sort(int a[], int start, int end) {
        if (start < end) {
            int mid = (start + end) / 2;
            sort(a, start, mid);
            sort(a, mid + 1, end);
            merge(a, start, mid, end);
        }

    }

    public void merge(int a[], int start, int mid, int end) {
        int temp[] = new int[end - start + 1];
        int i = start, j = mid + 1, k = 0;
        while (i <= mid && j <= end) {
            if (values[i] < values[j]) {
                temp[k++] = values[i++];
            } else {
                temp[k++] = values[j++];
            }
        }
        while (i <= mid) {
            temp[k++] = values[i++];
        }
        while (j <= end)
            temp[k++] = values[j++];
        for (k = 0; k < temp.length; k++) {
            values[start + k] = temp[k];
        }
    }

    @Override
    public void descSort() {
        // TODO Auto-generated method stub

    }

    public static void main(String[] args) {
        Random random = new Random();
        int[] arrays = new int[101];
        for(int i = 0;i<100;i++) {
            arrays[i] = random.nextInt(100000);
        }
         
        MergeSort mergeSort = new MergeSort(arrays);
        System.out.println("归并排序：升序排序");
        mergeSort.ascSort();
        mergeSort.print();
        System.out.println("归并排序：降序排序");
        mergeSort.descSort();
        mergeSort.print();
    }

}

排序结果：

 

基数排序

基数排序（radix sort）属于“分配式排序”（distribution sort），又称“桶子法”（bucket sort）或bin sort，顾名思义，它是透过键值的部份资讯，将要排序的元素分配至某些“桶”中，藉以达到排序的作用，基数排序法是属于稳定性的排序，其时间复杂度为O (nlog(r)m)，其中r为所采取的基数，而m为堆数，在某些时候，基数排序法的效率高于其它的稳定性排序法。

package com.geek.algorithm;

import static org.junit.Assert.assertEquals;

import java.util.Arrays;
import java.util.Random;

import org.junit.Test;

public class RadixSort extends BaseSort {

    public RadixSort(int[] values) {
        super(values);
        // TODO Auto-generated constructor stub
    }

    @Override
    public void ascSort() { 
        for (int i = 1; i <= getBitNum(); i++) {
            int temp[][] = new int[10][length];
            int tempindexs[] = new int[10];// 保存桶内的个数
            for (int j = 0; j < length; j++) {
                int num = getNumByBit(values[j], i); // 获取桶的下标 
                temp[num][tempindexs[num]] = values[j];
                tempindexs[num]++;
            }
            int x = 0;
            for(int j = 0;j<10;j++) {
                for(int k = 0;k<tempindexs[j];k++) {
                    values[x++] = temp[j][k];
                }
            }
        }
    }

    // 获取总位数
    public int getBitNum() {
        int max = 0;
        for (int v : values) {
            if (v > max) {
                max = v;
            }
        }
        int t = 0;// 计算位数
        while (max > 0) {
            max /= 10;
            t++;
        }
        return t;
    }

    // 查找指定位数的数 1个位 2十位
    public int getNumByBit(int num, int bitnum) {
        int t = 1;
        int result = 0;
        while (t <= bitnum) {
            result = num % 10;
            num /= 10;
            t++;
        }
        return result;
    }
    
    @Override
    public void descSort() {
        for (int i = 1; i <= getBitNum(); i++) {
            int temp[][] = new int[10][length];
            int tempindexs[] = new int[10];// 保存桶内的个数
            for (int j = 0; j < length; j++) {
                int num = getNumByBit(values[j], i); // 获取桶的下标 
                temp[num][tempindexs[num]] = values[j];
                tempindexs[num]++;
            }
            int x = 0;
            for(int j = 9;j>=0;j--) {
                for(int k = tempindexs[j]-1;k>=0;k--) {
                    values[x++] = temp[j][k];
                }
            }
        }
    }

    public static void main(String[] args) {
        Random random = new Random();
        int[] arrays = new int[10];
        for (int i = 0; i < 10; i++) {
            arrays[i] = random.nextInt(100000);
        }
        RadixSort radixSort = new RadixSort(arrays);
        System.out.println("基数排序升序：");
        radixSort.ascSort();
        radixSort.print();
        System.out.println("基数排序降序：");
        radixSort.descSort();
        radixSort.print();
        
        
    }
}

 排序结果 ：

 

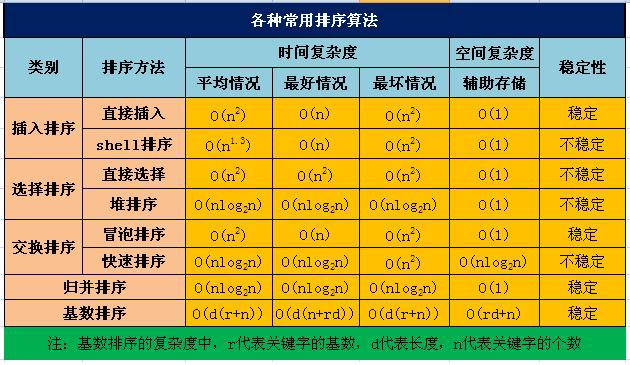
各种排序算法分析：