并查集

Posted 2020-10-16 ColdCode

一、定义

并查集是一种树形的数据结构，用于处理一些不相交集合的合并以及查询问题。

二、操作

1、void make_set(int n)

含义：有n个元素，把这n个元素初始化成n个集合，每个集合包含1个元素。

2、int find_root(int x)

含义：查找元素x所在的集合，返回集合的根结点。通过查找两个元素的根结点是否相同，可以判断两个元素是否属于同一个集合。

3、void union_set(int a, int b)

含义：合并两个不相交的集合。

三、举例

假设有3个元素，编号分别为1,2,3，则进行初始化make_set后，这3个元素形成了3个集合{1},{2},{3},集合之间互不相交，对应的树如下图所示：

可以看到3个元素形成了3颗独立的树，每颗树只包含一个根结点。我们使用数组p[x]来表示结点x的父结点，若x为根结点，则令p[x]=-1（或者令p[x]=x），所以有p[1]=-1,p[2]=-1,p[3]=-1。合并集合则是将一棵树的根结点变成另一颗树的孩子结点，合并集合{1},{2}后，对应的数如下所示：

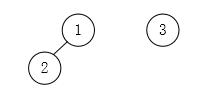
此时有p[1]=-1,p[2]=1,p[3]=-1。再将集合{3}与集合{1,2}合并，则有

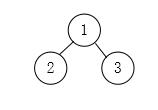
此时p[1]=-1，普p[2]=1,p[3]=1，3个集合最终合并成了一个集合。

四、优化

并查集最初的状态时一个个不相交的集合，如果只是简单的合并而不采取任何优化，那么树高可能会不断增加，最坏的情况是一棵树退化成了一条链，树高越高，查找根结点所花费的时间也就越长,我们希望树应该尽可能的低（两层），可以使用下面两种方法来进行优化：

1、路径压缩

在查找某结点x的根结点的过程中，将结点x与根结点和x之间的所有结点都直接指向根结点，这就是路径压缩。如下图：

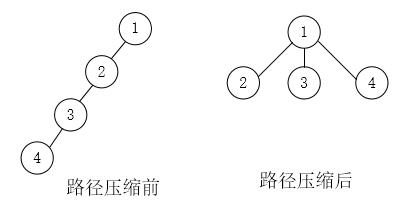
代码实现（递归）：

//查找根结点时路径压缩，递归实现
int find_root(int x)
{
    if(p[x] == -1)
        return x;
    else 
    {
        int t = find_root(p[x]);
        p[x] = t;
        return t;
    }
}

代码实现（非递归）：

//查找根结点时路径压缩，非递归实现
int find(int x)
{
    int k, j, r;
    r = x;
    while(r != p[r])     //查找跟节点
        r = p[r];      //找到跟节点，用r记录下
    k = x;        
    while(k != r)             //非递归路径压缩操作
    {
        j = [k];         //用j暂存parent[k]的父节点
        p[k] = r;        //parent[x]指向跟节点
        k = j;                    //k移到父节点
    }
    return r;         //返回根节点的值            
}

2、按秩合并

按秩合并即将元素少的集合合并到元素多的集合中，这样有利于降低树高。

五、代码实现

假设有n个元素，编号为1~n，现在输入这n个元素中的m个元素，输出最终建立的树中每个结点的父结点。

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <vector>
 4 using namespace std;
 5 
 6 const int N = 1000;
 7 int p[N];
 8 vector<int> v;  //存储输入的元素编号
 9 
10 int make_set(int n)
11 {
12     for(int i=1; i<=n; i++)
13         p[i] = -1;  //初始化，每个结点为一棵树
14 }
15 
16 int find_root(int x)
17 {
18     if(p[x] == -1)
19         return x;
20     else
21     {
22         int t = find_root(p[x]);    //路径压缩
23         p[x] = t;
24         return t;
25     }
26 }
27 
28 void union_set(int a, int b)
29 {
30     int ra = find_root(a);
31     int rb = find_root(b);
32 
33     if(ra != rb)    //a，b不在同一集合中，合并
34         p[ra] = rb;
35 }
36 
37 int main()
38 {
39     int n, m;
40     scanf("%d%d",&n,&m);
41     make_set(n);
42     int a, b;
43     scanf("%d", &a);
44     v.push_back(a);
45     for(int i=1;i<m;i++)
46     {
47         scanf("%d", &b);
48         v.push_back(b);
49         union_set(a, b);
50         a = b;
51     }
52 
53     for(int i=0; i<v.size(); i++)
54         printf("p[%d]=%d\\n", v[i], p[v[i]]);
55     return 0;
56 }

输入：

3 3
1 2 3

输出：

p[1]=2
p[2]=3
p[3]=-1

六、带权并查集

普通并查集只包含了结点与结点之间是否属于同一集合的信息，而带权并查集则加入了一个数组r[x]，记录了结点x与其父结点之间的信息（通常情况下），比如是否是同一类，有了多余的信息r[x]相当于结点x有了权值，这也是“带权”的含义。在进行路径压缩find_set和合并union_set时，r[]也要进行相应的变化，按秩合并就是带权并查集的一个应用。

七、例题

普通并查集：poj1611，poj2524，hdoj1232

带权并查集：poj2492，poj1703，poj1182