实验四:图及应用
课程:程序设计与数据结构
班级: 1623
姓名: 张旭升
学号:20162329
指导教师:娄嘉鹏 王志强
实验日期:11月22日
实验密级: 非密级
预习程度: 已预习
必修/选修: 必修
实验序号: cs_29
实验名称: 图的应用、实现和分析
实验内容:
1. 已实现的排序方法测试
2. 已实现代码重构
3. 补充查找算法
4. 补充排序算法
5. android实现排序查找
实验要求
1.没有Linux基础的同学建议先学习《Linux基础入门(新版)》《Vim编辑器》 课程
-
完成实验、撰写实验报告,实验报告以博客方式发表在博客园,注意实验报告重点是 运行结果,遇到的问题(工具查找,安装,使用,程序的编辑,调试,运行等)、解决 办法(空洞的方法如“查网络”、“问同学”、“看书”等一律得0分)以及分析(从中可 以得到什么启示,有什么收获,教训等)。报告可以参考范飞龙老师的指导
-
严禁抄袭,有该行为者实验成绩归零,并附加其他惩罚措施。
一、用邻接矩阵实现无向图
1.实验要求:
用邻接矩阵实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器给出伪代码,产品代码,测试代码
2.实现思路
根据添加结点的数量来建立一个结点的邻接矩阵(二维数组),如果两结点间存在边的话就将数组中对应的位置设置为
True反之则为False,然后以该邻接矩阵为基础来进行一些增删查改等操作。
3.关键代码解释
public boolean removeNode(T point){
int index = node.indexOf(point); //查询要删除结点的索引
boolean result = node.remove(point); //删除结点
become(index); //转换数组
return result;
}
private void become(int index){
boolean [][] m = new boolean[node.size()][node.size()];
for(int i=0;i<matrix.length;i++){
if(i!=index) {
int F = 0;
for (int j = 0; j < matrix[i].length; j++) {
if(j!=index) {
m[N][F] = matrix[i][j];
F++;
}
}
N++;
}
}
matrix = new boolean[node.size()][node.size()];
matrix = m;
}
所实现方法中只有删除结点的方法比较需要注意,因为结点和边是分开储存的,当你删除了结点时边的邻接矩阵是不改变的,索引我用了一个私有的改变数组的方法,当删除掉某个结点时同时将与它有联系的边一并删除且缩小矩阵矩阵。
4.测试截图

二、十字链表实现无向图
1.实验要求
用十字链表实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器给出伪代码,产品代码,测试代码
2.实验思路
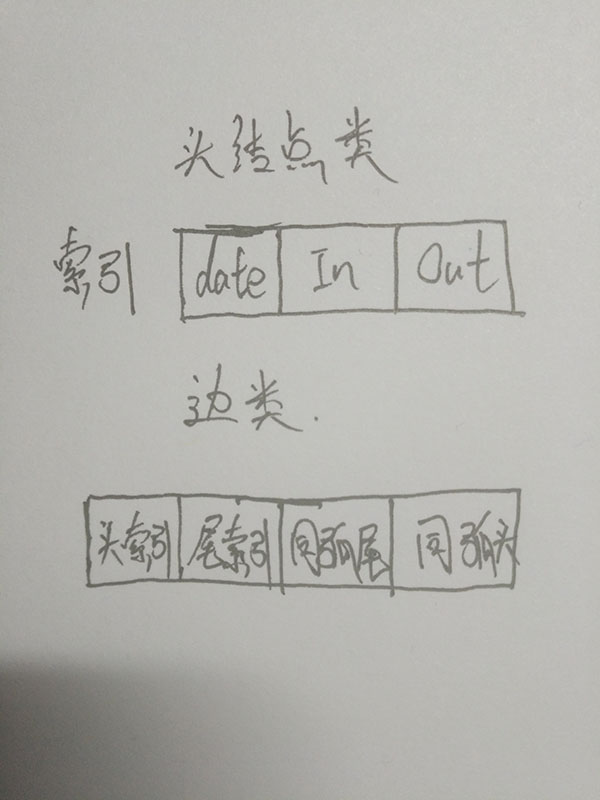
先分别创建头结点的类SZNode和边结点的类SZSide,两结点结构如下图:
通过添加结点和添加边的方法来构建一个图
3.关键代码解释
public boolean removeSide(E A,E B) throws Exception {
boolean result = false;
int num1 = -1,num2 = -1; //查找要删除边的索引
for(int i=0;i<node.size();i++){
if(node.get(i).data.equals(A))
num1 = i;
else if(node.get(i).data.equals(B))
num2 = i;
}
if(num1!=-1 && num2 != -1){
remove(num1,num2); //删边的方法
result = true;
}else
throw new Exception("找不到该边!");
return result;
}
与邻接矩阵不同的是,十字链表在删除边的时候是要特殊注意一个问题的,因为十字链表是以链表的形式,将边与头结点串联起来但是最终要的是每一个头结点并不止链接一条链,它的出边和进边都是链,所以我们需要设置两个头结点来遍历这两条边的链,然后在遍历中同时找到并删除相应的边。
4.测试截图

三、用图实现路由器的最短路径算法
1.实验思路
提示:我是基于十字链表设计的该算法,为了方便,在这里我把十字链表改为了实现有向图
具体思想如下:
当我们在查找图中某个结点到某个结点的路径的时候,先创建一个该点到其他点的路径长度的数组,然后通过代码运行比较,不断更新数组中路径从而找出最短路径。
2.关键代码解释
//查询最短路径
public String Min(E A,E B) throws Exception {
int num1 = -1,num2 = -1;
String result = null;
for(int i=0;i<node.size();i++){
if(node.get(i).data.equals(A))
num1 = i;
else if(node.get(i).data.equals(B))
num2 = i;
} //查询删除边的索引
S[num1] = 0; //更新路径数组,使得起始点自身路径长度为0
update(num1); //调用更新路径数组的方法
result = S[num2] + ""; //输出要查询的路径长度
restart(); //重置路径数组
if(result.equals("-1"))
result = "两结点间无路径!";
return result;
}
//更新最短路径数组
private void update(int num1){
SZSide head = node.get(num1).firstOut;
ArrayList<Integer> arr = find(num1);
while (head!=null&&!arr.isEmpty()){
int temp = head.toVertexIndex;
if(S[temp]==-1)
S[temp] = S[num1] + head.data;
else if(S[temp]>S[num1] + head.data){
S[temp] = S[num1] + head.data;
}
head = head.nextSameToVertex;
}
for (int i:arr)
update(i);
}
//查找相邻结点
private ArrayList<Integer> find(int num1){
ArrayList<Integer> arr = new ArrayList<>();
SZSide head = node.get(num1).firstOut;
while (head!=null){
if(!M[head.fromVertexIndex][head.toVertexIndex]) {
arr.add(head.toVertexIndex);
M[head.fromVertexIndex][head.toVertexIndex] = true;
}
head = head.nextSameToVertex;
}
return arr;
}
具体查询过程:输入要删除边的头尾结点名,查询头尾结点的索引,然后第一次更新路径数组,将除了该头结点位置以外的位置置为无限大(值为-1),然后调用更新方法,在更新方法中先查找与该点相连的点的索引,然后将两点之间的边的权值赋给路径数组中相应的位置,然后再以该点再次查找相邻点(递归实现),知道都每个点都查找完为止。
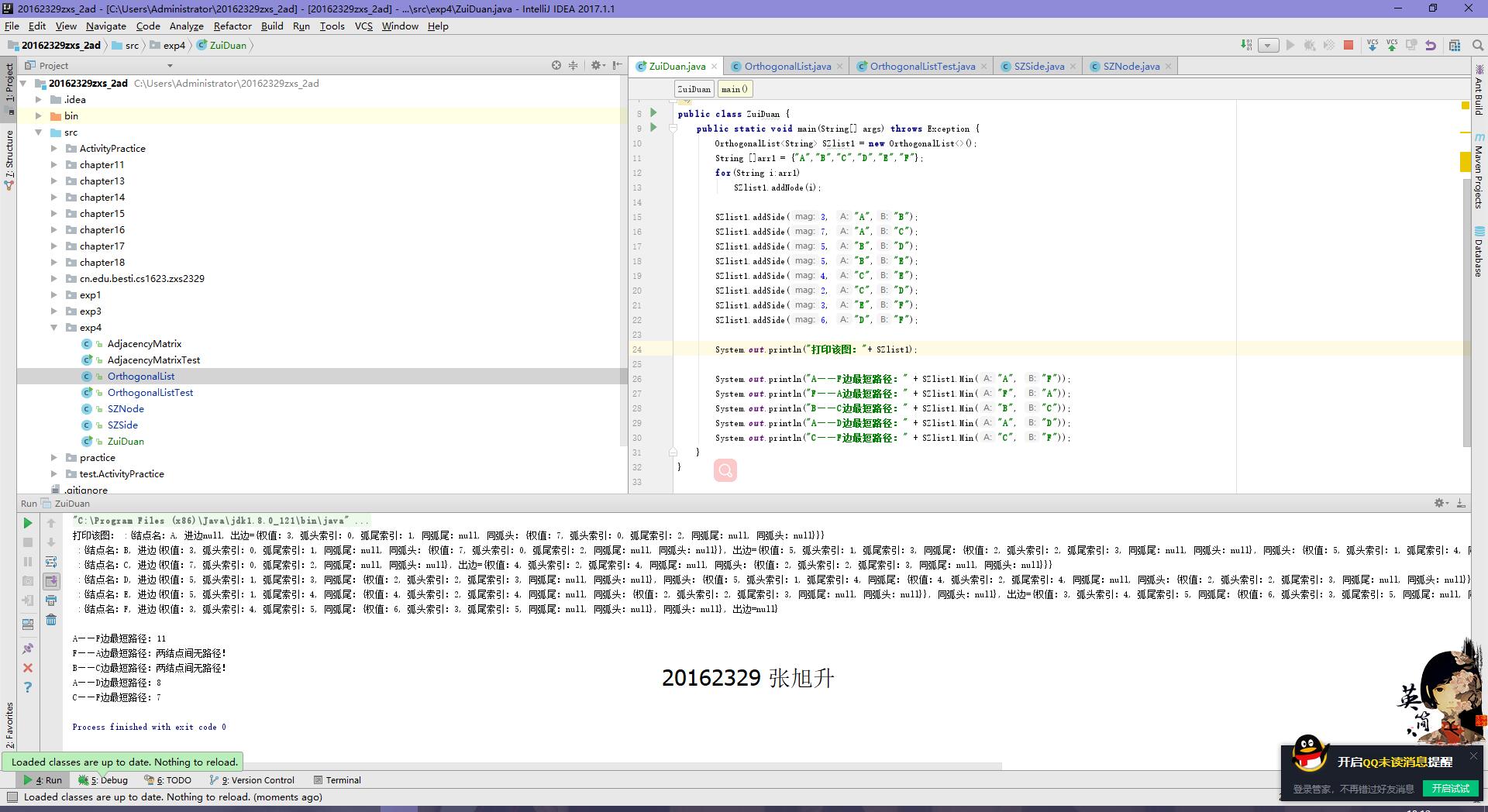
3.测试截图
四、实验心得
这次实验完全是通过自己以往学到的知识完成的,当自己实现一个算法的时候不仅会有一种莫名的成就感,而且同时还回顾了之前的知识,尤其是在链表方面,通过本次实验又得到了巩固。