实验四-图的实现与应用

Posted 2020-10-15

实验四-图的实现与应用

图的实现与应用-1

实验要求：

用邻接矩阵实现无向图（边和顶点都要保存），实现在包含添加和删除结点的方法，添加和删除边的方法，size(),isEmpty()，广度优先迭代器，深度优先迭代器

实验过程：

1. 用二维数组构建邻接矩阵
2. 添加删除边的方法和添加顶点的方法的较为简单，在此不做介绍
3. （重点）删除顶点：利用两个for循环；外层循环遍历列，内层循环遍历排。
   伪代码如下：

public void removevertice(int A){
for（int i = 0； i < 数组长度;i++）{
    for（int i = 0； i < 数组长度;i++){
        if (i 等于 A 并且 该二维数组的值为真)
        该二维数组的值为假
        if(s 等于 A)
        该二维数组的值为假
    }
}
}

4.广度遍历：参考书上代码：在书上代码的基础进行微调。伪代码：

定义一个数组visited，用于存放已标记顶点
for 将顶点放入visited数组中并将其标注为未访问
将顶点入队并标记为已访问
while（队列不为空）｛
从队列中取出第一个顶点，并将顶点放入list中
，将当前顶点中未被标记为以访问的所有邻接点入队，同时将这些顶点标记为已访问
｝

5.深度遍历：用栈替换队列

实验结果：

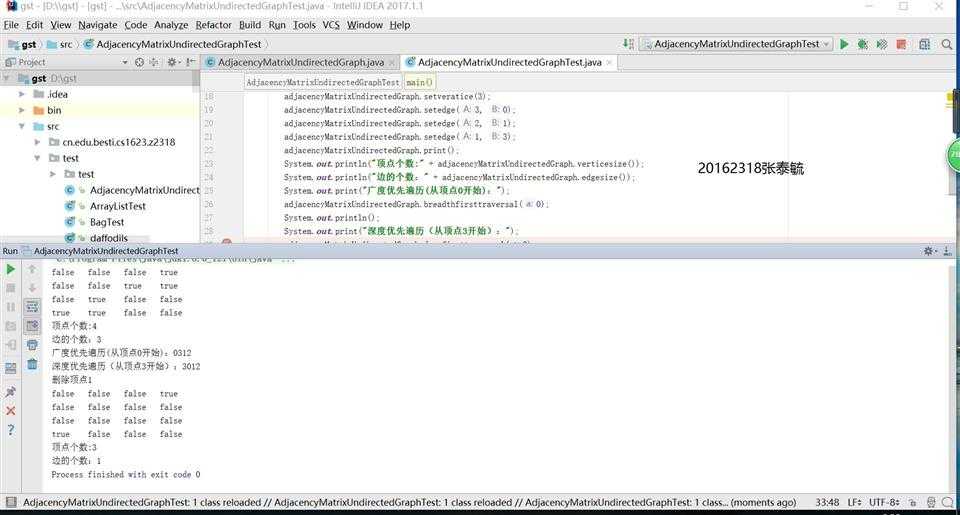
代码链接

图的实现与应用-2

实验要求：

用十字链表实现无向图（边和顶点都要保存），实现在包含添加和删除结点的方法，添加和删除边的方法，size(),isEmpty()，广度优先迭代器，深度优先迭代器

实验过程：

刚开始对十字链表这个结构不是十分的了解，简单的来说十字链表就是两个链表结合在一块，织成一张网。或者可以这样理解：它其实也是一个邻接矩阵，只不过它是特殊的：

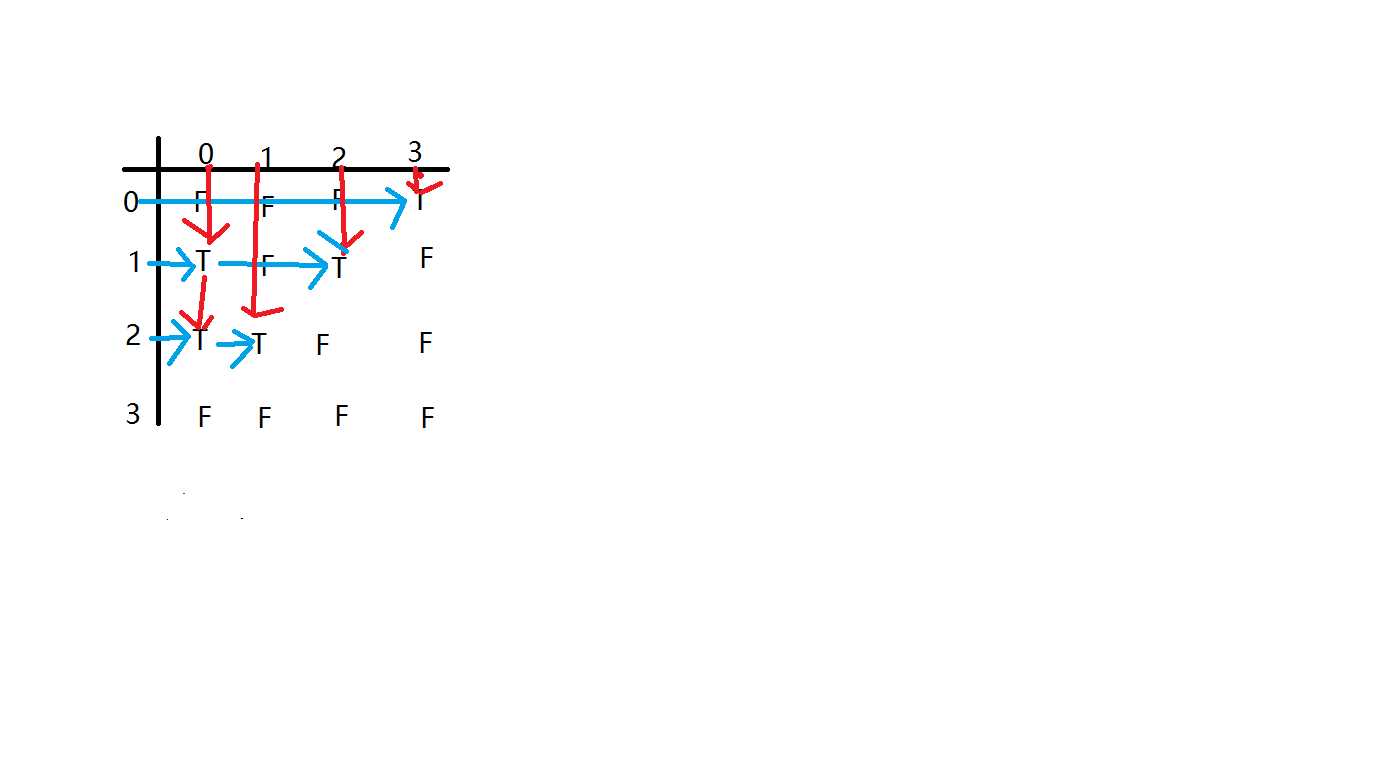
定义顶点结构：

定义边结构：

构件图思路与构建链表的思路换汤不换药，其中较为麻烦的便是删除顶点，下面给出源代码：

public void removeVertic(VertexNode node) {
        list.remove(node.getVertex());
        EdgeNode edgeNode1 = node.firstOut;
        EdgeNode edgeNode2 = node.firsstIn;
        while (edgeNode1 != null) {
            removeEdge(edgeNode1);  //删除边
            edgeNode1 = edgeNode1.taillink;
        }
        while (edgeNode2 != null) {
            removeEdge(edgeNode2); //删除边
            edgeNode2 = edgeNode2.headllink;

        }
    }

实验结果：

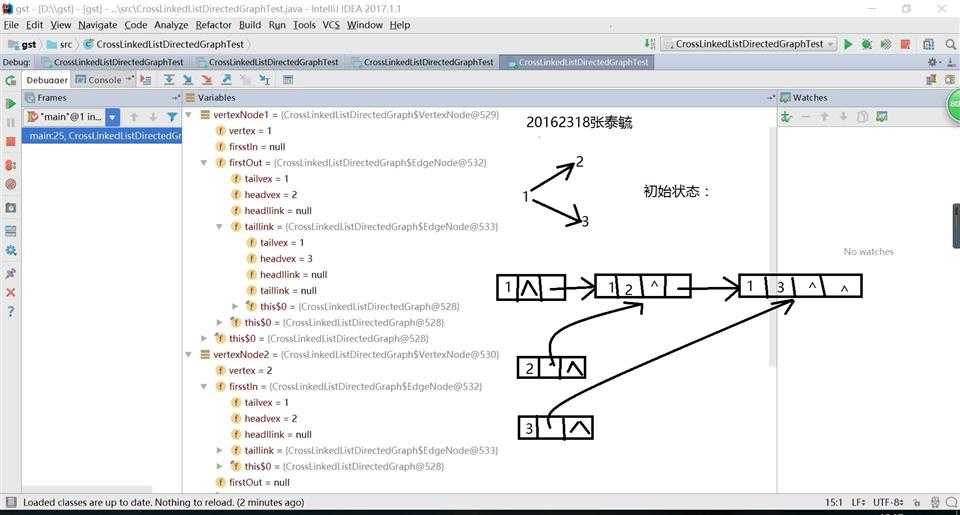
代码链接

图的实现与应用-3

实验要求：

实现PP19.9

实验过程

此题我选用弗洛伊德算法

弗洛伊德算法：通过一个图的权值矩阵求出它的每两点间的最短路径矩阵。

伪代码：

（1）设Dist(u, v)为结点u到结点v的距离，中间点w，
（2）若有Dist(u, w) + Dis(w, v) < Dis(u, v)，则Dis(u, v) = Dis(u, w) + Dis(w, v)，
（3）遍历所有顶点w，Dis(u, v)中记录的便是u到v的最短路径的距离

核心代码：

for (int k = 0; k < dis.length; k++) {
            for (int i = 0; i < dis.length; i++) {
                for (int j = 0; j < dis.length; j++) {
                    int mn = dis[i][j];
                    int mk = dis[i][k];
                    int kn = dis[k][j];
                    int addedPath = (mk == MAX_WEIGHT || kn == MAX_WEIGHT) ? MAX_WEIGHT : mk + kn;

                    if (mn > addedPath) {
                        //如果经过k顶点路径比原两点路径更短，将两点间权值设为更小的一个
                        dis[i][j] = addedPath;
                        //前驱设置为经过下标为k的顶点
                        path[i][j] = path[i][k];
                    }
                }
            }
        }

实验结果：

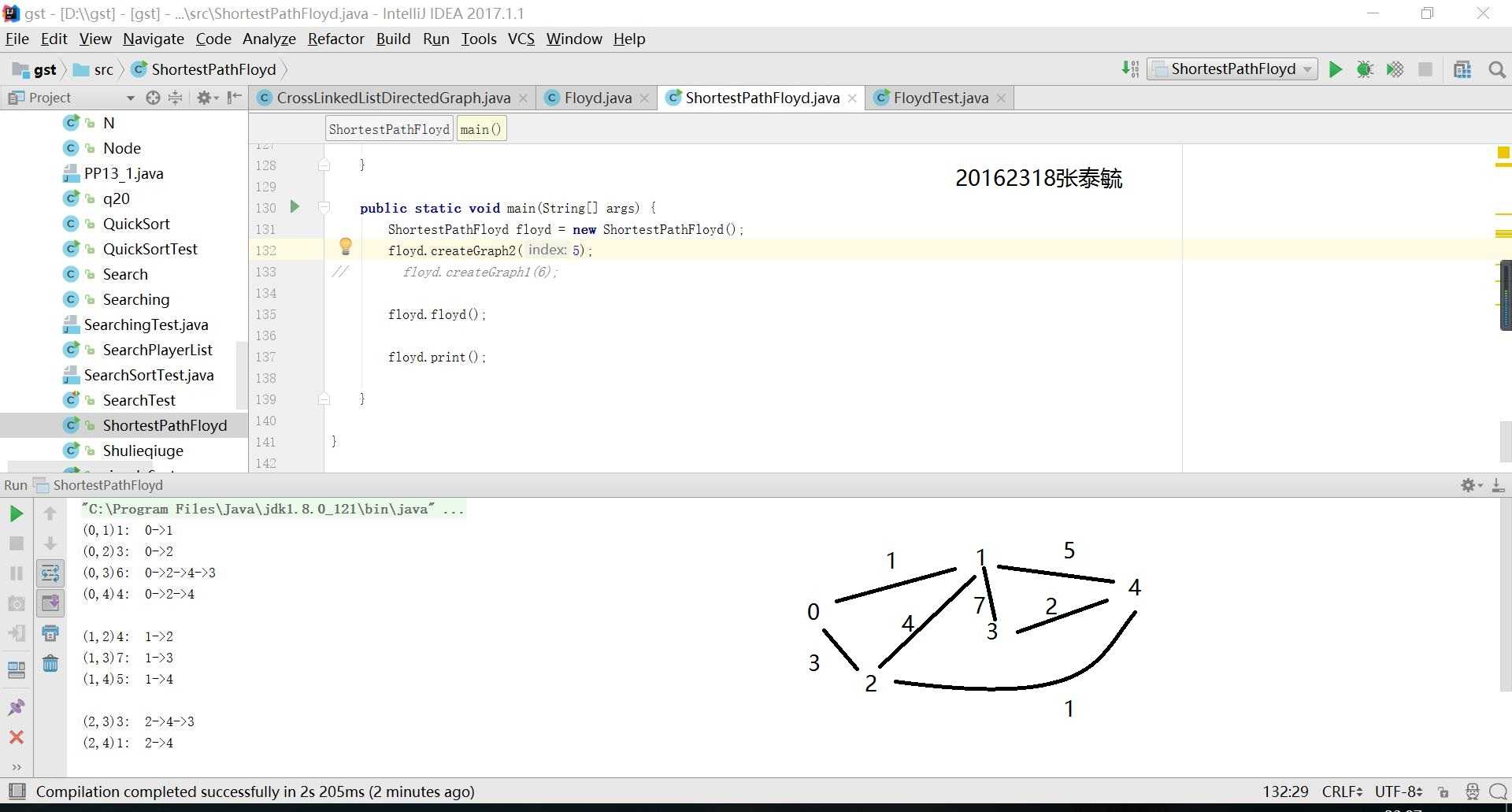
代码链接