实验四-图的实现与应用
实验四 图的实现与应用-1
试验内容
用邻接矩阵实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器
给出伪代码,产品代码,测试代码(不少于5条测试)
实验结果
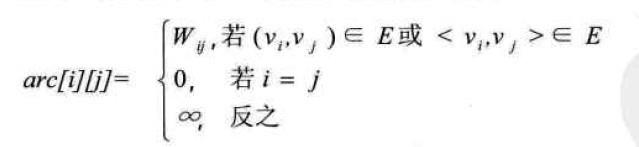
- 要想用邻接矩阵实现图,首先需要使用一个一维数组存放顶点,一个二维数组存放边;
- 然后清楚两个顶点之间的关系如何表示,用邻接矩阵表示出来是什么样的;
- 其中值得注意的是对角线上的应该是0,因为自己和自己是没有路径的。

广度优先遍历
设立一个访问标志数组visited[N],初值为0,某顶点被访问后,则相应下标元素置1。
(1)初始化队列Q;visited[N]=0;
(2)访问顶点v;visited[v]=1;顶点v入队列Q;
(3) while(队列Q非空)
v = 队列Q的队头元素出队;
w = 顶点v的第一个邻接点;
while ( w存在 )
如果w未访问,则访问顶点w;
visited[w]=1;
顶点w入队列Q;
w=顶点v的下一个邻接点
深度优先遍历
设立一个访问标志数组visited[N],初值为0,某点被访问,则相应下标变量置1。
输入要访问的结点V1;
访问结点V1,visited[vi]=1;
在邻接矩阵第i行中进行查找,若vi有邻接点vj没有被访问,则设置vi=vj;
重复前几步直到所有结点均被访问;
实验四 图的实现与应用-2
实验内容
用十字链表实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器
给出伪代码,产品代码,测试代码(不少于5条测试)
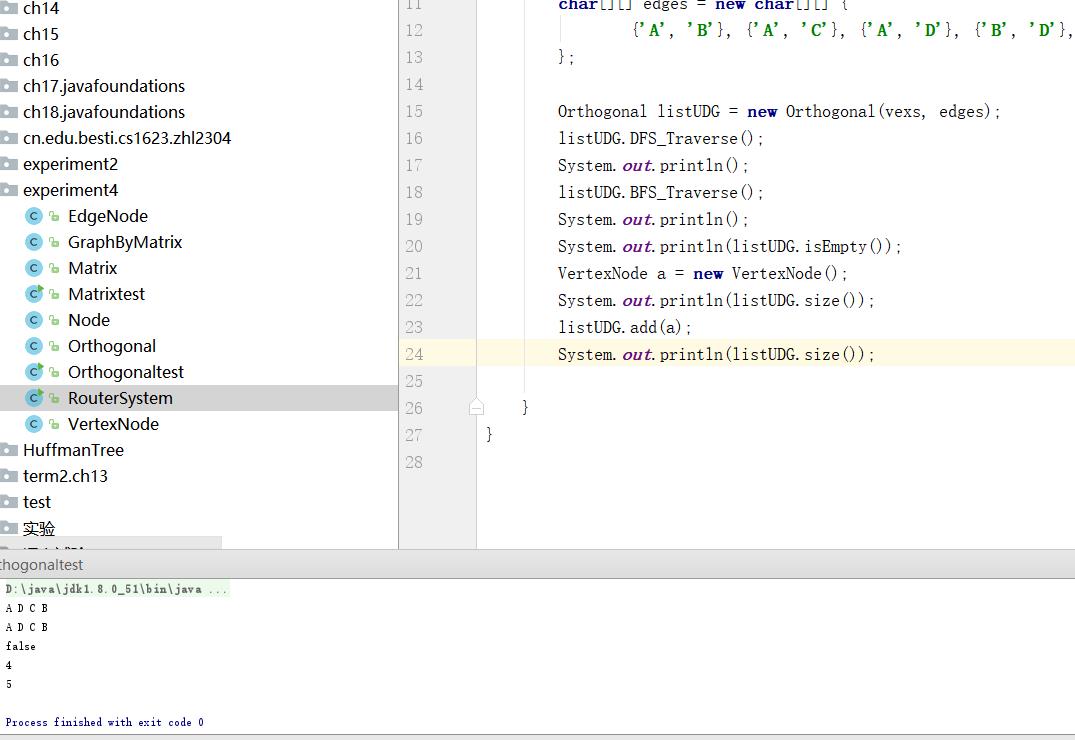
实验结果
- 十字链表的概念:十字链表(Orthogonal List)是有向图的另一种链式存储结构。该结构可以看成是将有向图的邻接表和逆邻接表结合起来得到的。用十字链表来存储有向图,可以达到高效的存取效果。同时,代码的可读性也会得到提升。
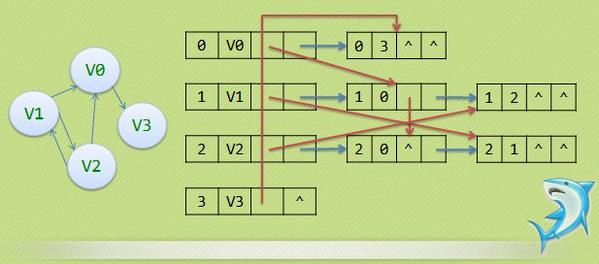
在这个实验中我们说一下具体方法的实现
1.add()
这个方法的话,我直接让数组的下一个位置等于我们输入的那个元素;
2.isEmpty()
在这里只需要判断我们用于储存结点的数组是否为空即可。
3.size()
返回用于计数的 anInt;
4.remove()
这个方法在十字链表这块儿我到目前为止还没能实现,希望可以通过继续的学习实现。
实验四 图的实现与应用-3
实验内容
实现PP19.9
给出伪代码,产品代码,测试代码(不少于5条测试)
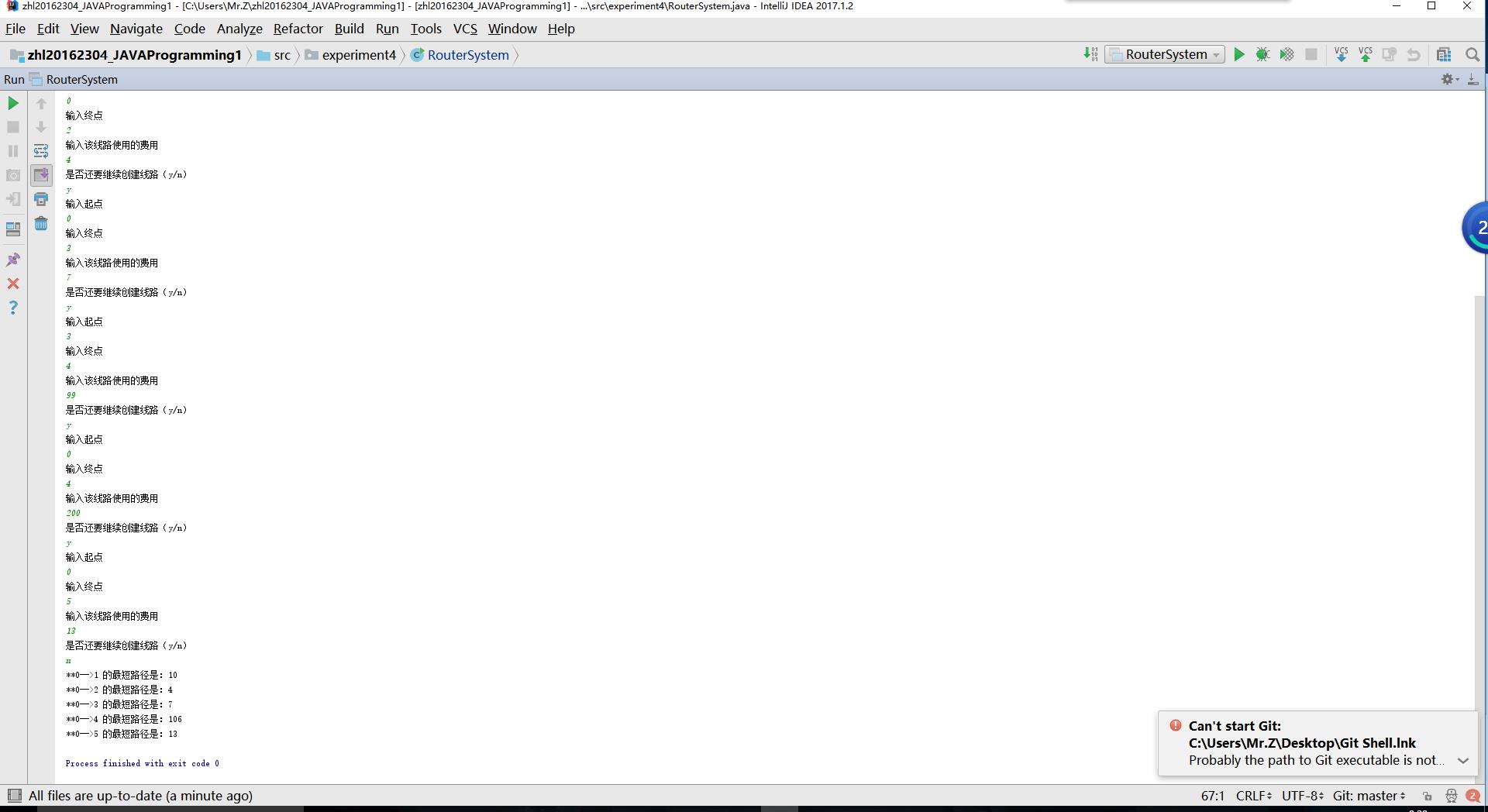
实验结果
PP19.9,只需要调用前面我们实现的树的遍历,然后在其中加入判断如何判别最短路径的方法即可,
判断最短路径的方法:
开始假定直达路径即为我们需要的最短路径
初始时v0属于visited,即已经找到v0 到v的最短路径
来假设经由一个点中转到达其余各点,会近些并验证
直到我们穷举完
挑一个距离最近经由点,下标装入 v
经由顶点j中转则距离更短
顶点v并入S,由v0到达v顶点的最短路径为min.
假定由v0到v,再由v直达其余各点,更新当前最后一个经由点及距离
如果多经由一个v点到达j点的 最短路径反而要短,就更新
实验中遇到的问题
1.实验中遇到的一个比较突出的问题就是,在我写实验1测试类的时候遇到了死循环
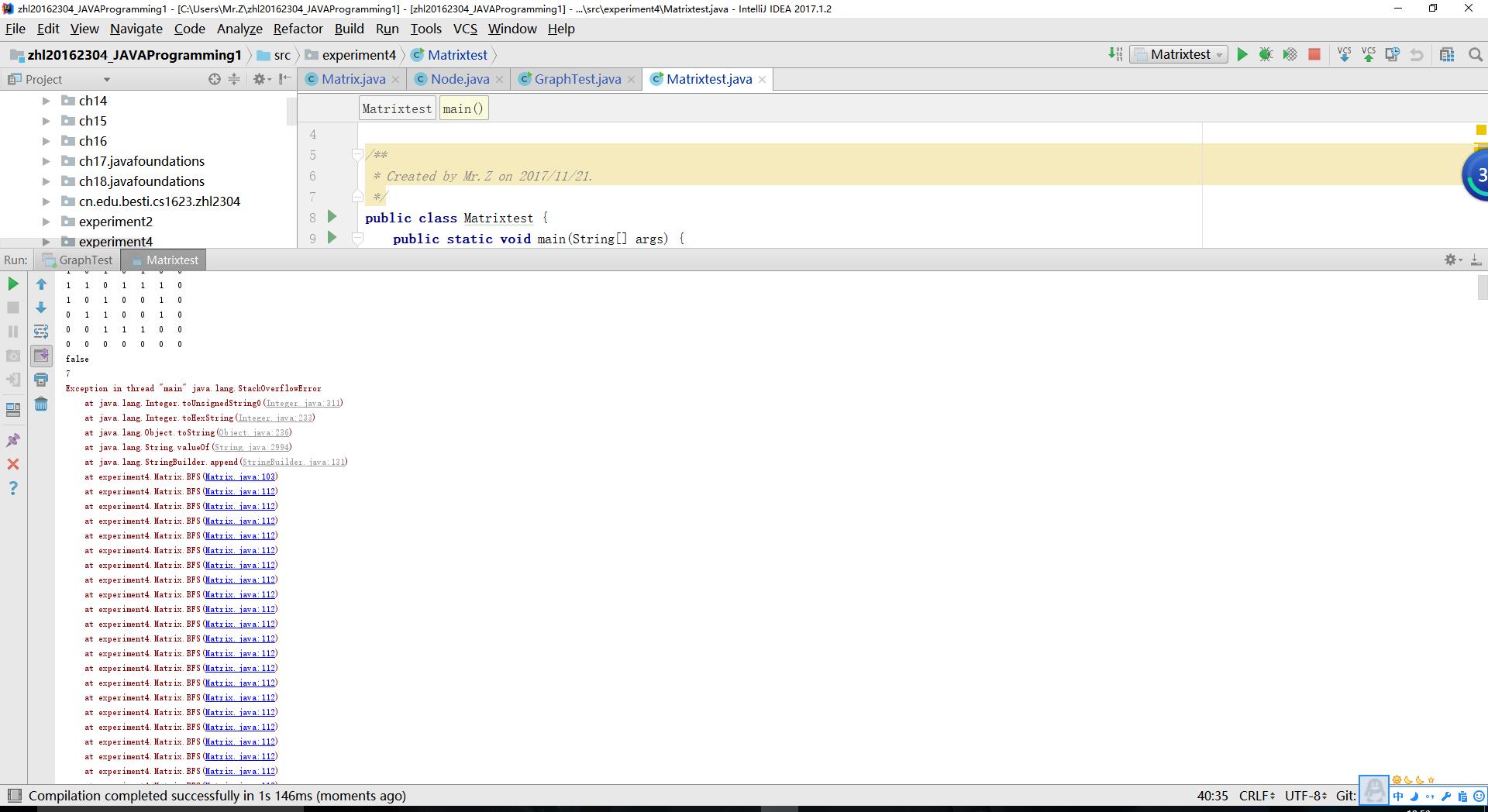
解决过程:经过反复尝试我发现是在添加数据进去的时候没有正确的改变数组的大小从而导致死循环
2.实验3实现的过程中出现了空指针的问题
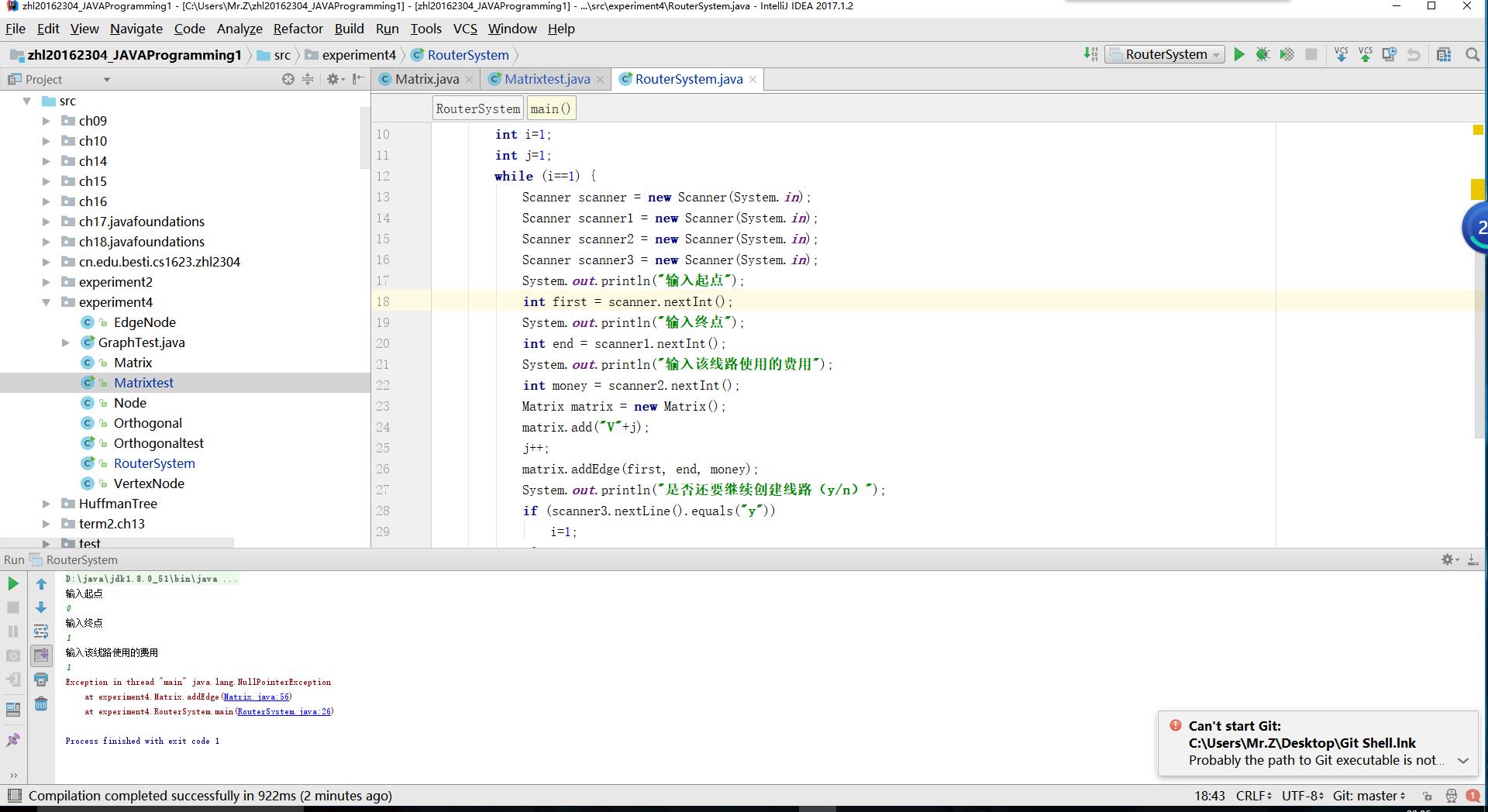
这个问题,在求助杨京典同学后,我们发现,我是没有先将点加到数组中,就先开始在两点之间建立连线了,将顺序换一下,就改好啦
实验感悟
这次实验给我的收获比较大,遇到了一些以前没有主要到的问题,老师也及时为我指出了我的不足,我会在以后注意这些问题的。