吴恩达-深度学习-课程笔记-6: 深度学习的实用层面( Week 1 )
Posted PilgrimHui
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了吴恩达-深度学习-课程笔记-6: 深度学习的实用层面( Week 1 )相关的知识,希望对你有一定的参考价值。
1 训练/验证/测试集( Train/Dev/test sets )
构建神经网络的时候有些参数需要选择,比如层数,单元数,学习率,激活函数。这些参数可以通过在验证集上的表现好坏来进行选择。
前几年机器学习普遍的做法: 把数据分成60%训练集,20%验证集,20%测试集。如果有指明的测试集,那就用把数据分成70%训练集,30%验证集。
现在数据量大了,那么验证集和数据集的比例会变小。比如我们有100w的数据,取1w条数据来评估就可以了,取1w做验证集,1w做测试集,剩下的用来训练,即98%的训练集。对于数据量过百万的数据,训练集可以占到99.5%
我们在做一个应用的时候,比如训练一个分类器识别猫,可能训练集数据都是网上爬取的,验证集和测试集都是用户上传的,这样训练集的分布和验证测试集的分布不一致。
这种情况,有一条经验法则,建议大家要确保验证集和测试集的数据来自同一分布,因为你要用验证集来评估不同的模型。而训练集因为要收集大量数据,可以采用各种方法比如网页抓取,这样会导致训练集和验证测试集分布不一致。
测试集是对模型的无偏估计,没有测试集的话就是在训练集上训练,在验证集上评估然后修改参数迭代出适用的模型。有些团队说他们的设置中只有训练集和测试集,而没有验证集。这样的训练实际上就是只有训练集和验证集,并没有用到测试集的功能。
2 偏差和方差( bias / variance )
高偏差:数据拟合的不好,欠拟合,比如在训练集和验证集上的效果都差,训练集和验证集准确率差不多
高方差:数据拟合的太好而泛化能力变差,过拟合,比如在训练集上表现好,在验证集上表现差,训练集和验证集的准确率相差甚多
高偏差和高方差:训练集上表现很差,验证集上表现更加差,训练集和验证集的准确率相差甚多。高方差和高偏差的数据样本见下图所示。
这里有个假设前提:训练集和验证集来自同一分布。
表现好不好相对于最优误差来讲的,比如猫的二分类,人能够几乎0%的错误率识别是不是猫,那么最优误差是0%,这个时候训练误差和验证误差都是16%,可以判定为高偏差。
如果一个问题的最优误差是15%,那么训练误差和验证误差都是16%,就不能说它高偏差。

3 机器学习基础( Basic recipe for machine learning )
训练集表现不好,高偏差:重新构建网络,更多隐藏层,更多隐藏单元,迭代更多次,更改优化器等等,必须做各种尝试(可能有用,可能没用)。反复尝试,直到可以拟合数据为止。如果网络空间很大,通常可以很好的拟合数据集。
过拟合,高方差:尽可能使用更多的数据,正则化,同样要做各种反复的尝试。
在深度学习早期,没办法做到只减少偏差或方差却不影响另一方。
但当前的深度学习和大数据时代,只要有足够大的网络,足够多的数据(也不一定只是这两个,只是做个假设),就可以在不影响方差的同时减少偏差。
4 正则化( Regularization )
在原始的损失函数后面加一个正则项,主要是权重w的L2范式的平方,此方法称为L2正则,实际上L2正则在进行梯度下降的时候做了一个权重衰减,从公式上可以看出。
也可以用L1正则,加上的是w的L1范式,就是绝对值相加,它可以使w稀疏,也就是w有很多0。
正则化就是对权重w进行惩罚,当w太大的时候损失函数会变大,这个时候优化为了使损失函数尽可能小就会惩罚w,减小了w的影响,使神经网络变得简单,由此来防止过拟合。
也可以这样理解,正则使得w尽量小,这个时候z就比较小,比如对于激活函数tanh来说,z比较小的时候梯度相对来说比较像一条直线,那么得到的函数相对呈线性,这样整个神经网络就不会过于复杂,由此来防止过拟合。

5 dropout正则( Dropout regularization )
除了L2正则,还可以用dropout正则来防止过拟合。
dropout会在每一层随机删除一些节点,相当于直接使某些层的权重为0,由此使得网络规模变小,得到一个精简后的网络。
对于每一个样本都会用一个精简后的网络训练,这样的话可以认为每个样本训练时的网络结构是不一样的。
具体如何实施呢?有几种方式,ng讲了常用的一种,Inverted dropout反向随机失活。
对于模型的某一层,设定一个概率keep-prob表示保留单元的概率。生成一个随机矩阵,表示每个样本和每个隐藏单元是否丢弃:$d^{[3]} = np.random.rand( d^{[3]}.shape[0], d^{[3]}.shape[1]) < keep-prob$
过滤掉$d^{[3]}$中所有等于0的元素:$a^{[3]} = np.multiply( a^{[3]}, d^{[3]} )$
dropout后需要把所有数值除以这个保留概率(为了保证a3的期望不变):$a^{[3]} /= keep-prob$
测试阶段不使用dropout,因为我们在测试阶段不希望输出的结果是随机的。
另一个dropout有效的直观理解是,因为对于某个单元,输入单元有可能被删除,所以神经网络不会分配太大的权重,这相当于L2正则中的收缩权重的效果,所以说dropout的功能类似于L2正则。
每层的keep-prob可以不同,对于单元数多,容易过拟合的层可以用小一点的keep-prob,对于不容易过拟合可以用大一点的keep-prob。
很多dropout的第一次成功应用是在计算机视觉领域,因为计算视觉中往往输入了过多的像素。计算机视觉的研究人员很喜欢用dropout,几乎成了默认的选择。
但是要记住,dropout是为了防止过拟合的手段,当算法过拟合的时候才使用,所以一般是用在计算视觉方面(往往没有足够的数据,容易过拟合)。
dropout的一大缺点就是代价函数不再被明确定义,每次迭代都会随机移除一些节点,很难调试梯度下降的迭代过程(绘制迭代次数和cost的函数图)。
可以在调试的时候先把keep-prob设置为1,绘制出迭代图,之后再打开dropout。
6 其它正则化方法( Other regularization methods)
数据增强(data augmentation),对原始图像做一些翻转,裁剪,放大,扭曲等处理,产生额外的数据,这些额外的数据可能无法提供太多的信息,但是这么做没什么花费(相比于收集新数据要简单的多)。
提早停止(early stopping), 当发现验证集降到最低开始上升的时候(表示要过拟合了),这个时候停止训练,可以理解为选择一个中等的w来防止过拟合(一开始随机初始化很小,随着训练慢慢增大)。
early stopping有一个缺点,就是它无法同时处理最小化代价和防止过拟合这两个问题(防止了过拟合,但是可能早早就停下来了,没有做到最小化代价)。
所以代替early stopping用的L2正则,这样训练的时间就可能很长,你必须尝试很多正则化参数,搜索参数的计算代价太高。而early stopping的优点就是无需尝试很多参数。个人倾向于用L2正则。

7 归一化输入( Normalizing inputs)
归一化输入需要两个步骤:零均值化和归一化方差。
零均值化:样本中的每个特征值都减去该特征 的平均值,这样每个特征的均值为0。
归一化方差:样本中每个的特征值除以该特征的方差,这样每个特征的方差为1。
值得注意的是,如果你在训练集归一化,那么在测试集要用相同的平均值和方差(训练集计算得到的)来归一化,因为我们希望在训练集和测试集上做相同的数据转换。
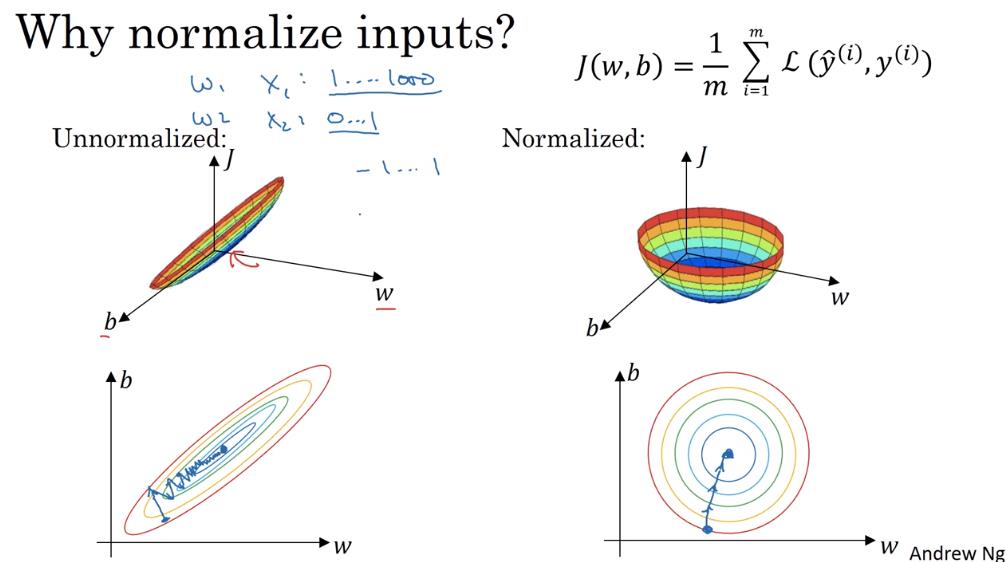
为什么要归一化输入特征呢?如下第1个图左侧所示,如果不归一化的话,代价函数可能是一个非常细长狭窄的函数,在训练的时候需要设置很小的步长,迭代时间会变长。
如下第1个图右侧所示,归一化后,各个特征都在相似范围内,代价函数更圆,更容易优化,梯度下降法能够使用较大的步长,更快速地迭代。

8 梯度消失,梯度爆炸,权重初始化( Vanishing / exploding gradients,Weight initialization for deep networks )
ng的例子中,训练神经网络的时候如果网络很深的话,假设权重都是1.5,传递到最后一层的y的值将会呈指数增长(因为每经过一层就会乘一个权重1.5),假设权重都是0.5,传递到最后一层的y将会变得很小很小。
这是造成梯度消失或梯度爆炸的原因,它给训练造成了很大困难。针对梯度消失或梯度爆炸,有一个不完整的解决方案,虽然不能彻底解决问题,却很有用。
考虑$z = w_1*x_1 + w_2*x_2 + ... + w_n*x_n$,为了防止z太大或太小,可以看到n越大的话,你就希望w越小,以此来平衡z,那么很合理的设定就是把w设定为1/n。
所以在某一层,初始化权重的方法就是设定值为$\\sqrt{\\frac{1}{n^{[l-1]}}}$,如下图所示,其中$n^{[l-1]}$表示l层的输入特征数。如果你使用的是relu激活,那么用2 / n效果会更好。
此外,还有一些其它的变种,见下右图所示。权重初始化可以看做一个超参数,但是相比于其它超参数,它的优先级比较小,一般优先考虑调整其它超参数来调优。

9 梯度的数值逼近,梯度检验( Weight initialization for deep networks, Gradient Checking )
进行梯度检验的时候,考虑某点前进很小很小距离的点,和往后很小小距离的点,考虑了两个点估计的梯度会更准确,渐进误差为这段距离的平方O(ε^2)。
考虑某点前进很小很小的一段距离的点来估计梯度,只考虑了单边,渐进误差为这段距离O(ε)。
所以我们采用双边误差的估计来进行梯度检验,用双边误差的估计梯度和实际求导的梯度做一个距离计算,看看距离是否足够小。
ng介绍的梯度检验如下第2个图所示,其中Θ[i]表示第i个样本的所有权重,距离公式中的分母只是为了防止数值太大而加的。
需要注意的是,梯度检验和dropout不要同时进行,


以上是关于吴恩达-深度学习-课程笔记-6: 深度学习的实用层面( Week 1 )的主要内容,如果未能解决你的问题,请参考以下文章
下载量过百万的吴恩达机器学习和深度学习笔记更新了!(附PDF下载)
吴恩达 DeepLearning.ai课程笔记(1-3)神经网络和深度学习 --- 浅层神经网络
吴恩达-深度学习-课程笔记-1 Introduction to Deep Learning( Week 1)