OJ1147括号匹配加强版(栈)
Posted YuWenjue
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了OJ1147括号匹配加强版(栈)相关的知识,希望对你有一定的参考价值。
惨兮兮的被刷掉2%的通过率后在经过思考和dalao的指点后终于A掉了这道题
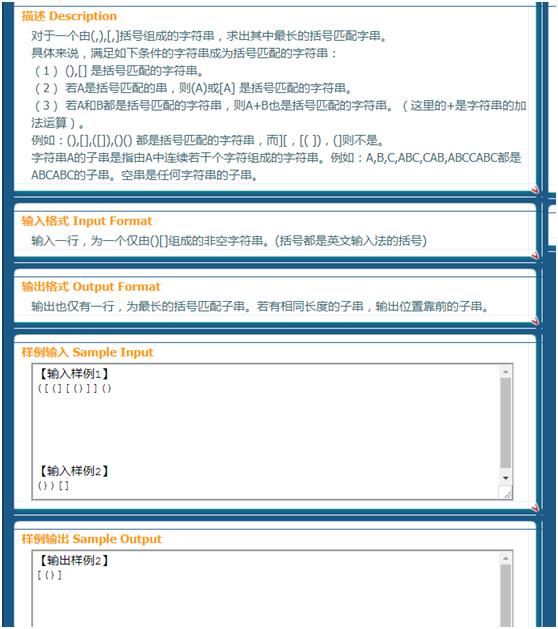
强烈建议修改这题的样例,实在太迷惑人,各种错误算法都能过
比如说这是一份错误代码,看懂了也不要学思路,和正解不知道差到哪里去了:
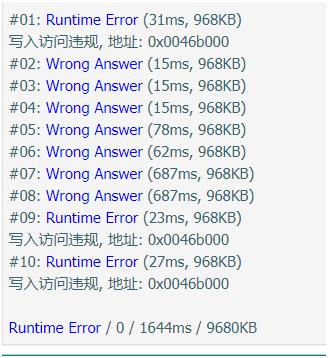
惨兮兮,WA掉代码:
#include <iostream>
#include <iomanip>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <ctime>
using namespace std;
char a[100086];
int len,top=0,ll=0,lexn,maxx=-10000,leen;
char s[100086],bb[10086],jg[100086];
bool f=true;
int main()
{
memset(a,0,sizeof(a));
memset(s,0,sizeof(s));
cin>>a;
len=strlen(a);
for(int i=0;i<len;i++)
{
if(s[top]==\'(\')
{
if(a[i]==\']\')
{memset(s,0,sizeof(s));memset(bb,0,sizeof(bb));top=0;f=false;}
else if(a[i]==\'(\')
{
s[++top]=a[i];
bb[++ll]=a[i];
}
else if(a[i]==\')\')
{
bb[++ll]=a[i];
top--;
}
}
else if(s[top]==\'[\')
{
if(a[i]==\')\')
{memset(s,0,sizeof(s));memset(bb,0,sizeof(bb));top=0;f=false;}
else if(a[i]==\'(\')
{
s[++top]=a[i];
bb[++ll]=a[i];
}
else if(a[i]==\']\')
{
bb[++ll]=a[i];
top--;
}
}
else if(a[i]==\'(\'||a[i]==\'[\')
{s[++top]=a[i];bb[++ll]=a[i];}
if(top==0&&f)
{
//lexn=strlen(bb);
if(maxx<ll)
{
memset(jg,0,sizeof(jg));
maxx=ll;
if(leen!=maxx)
leen=0;
for(int i=1;i<=ll;i++)
{
jg[i]=bb[i];
leen++;
}
}
ll=0;
memset(bb,0,sizeof(bb));
memset(s,0,sizeof(s));
}
if(!f)
f=true;
}
for(int i=1;i<=leen;i++)
{
if(jg[i]==\'[\'||jg[i]==\'(\'||jg[i]==\']\'||jg[i]==\')\')
cout<<jg[i];
}
return 0;
}(这是WA掉的)
但即便是这个WA掉所有数据的错误代码都能过样例,所以改一下为好吧……
然后是正解思路:
读入一个char型数组,然后将此数组中的字符挨个进栈,如果栈顶为’]’或是’)’,查看第top-1个元素,如果是能与当前字符匹配的左括号,就出栈,bool型数组标记下标,否则就将栈清空,然而操作还是讲不清,代码如下:
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <ctime>
#include <algorithm>
using namespace std;
int len,s=0,maxx=-1000,top=-1,sum=-1,num=-1,t=0;//top为栈顶下标,因为是字符串,所以为-1,sum,num同理
char a[1000086],stack[1000086];
bool f[1000086];
int d[1000010],e[1000010];//开两个数组分别记录\'(\'和\']\'的下标
int main()
{
cin>>a;
memset(f,false,sizeof(f));
len=strlen(a);
for(int i=0;i<len;i++)
{
stack[++top]=a[i];//入栈
if(stack[top]==\'(\')//当栈顶是(时,记录下标
d[++sum]=i;
if(stack[top]==\'[\')//同上
e[++num]=i;
if((stack[top]==\')\'&&stack[top-1]==\'[\')||(stack[top]==\']\'&&stack[top-1]==\'(\'))//当右括号与栈顶左括号不匹配时,栈清空
top=0;
else if((stack[top]==\')\'&&stack[top-1]==\'(\')||(stack[top]==\']\'&&stack[top-1]==\'[\'))//当栈顶左括号与右括号匹配时
{
f[i]=1;//标记当前下标
if(stack[top]==\']\')//如果栈顶右括号为]?
{
f[e[num]]=1;//bool数组标记下标
num--;//存储]的数组减去一个]
}
if(stack[top]==\')\')//理同上
{
f[d[sum]]=1;
sum--;
}
top-=2;//因为左括号与右括号匹配,所以直接删去两个
}
}
for(int i=0;i<len;i++)
{
if(f[i])//t为能够匹配的括号式的长度
t++;
else//因为匹配括号式必须挨着,所以一旦!f[i],则说明已经记录完了一个括号式
{
if(t>maxx)//标记最大长度
{
maxx=t;
s=i;//s记录当前下标
}
t=0;
}
}
if(t>maxx)//避免式子在最后
{
maxx=t;
s=len;
}
for(int i=s-maxx;i<s;i++)//s减去maxx即为最长表达式的起始下标
cout<<a[i];
return 0;
}
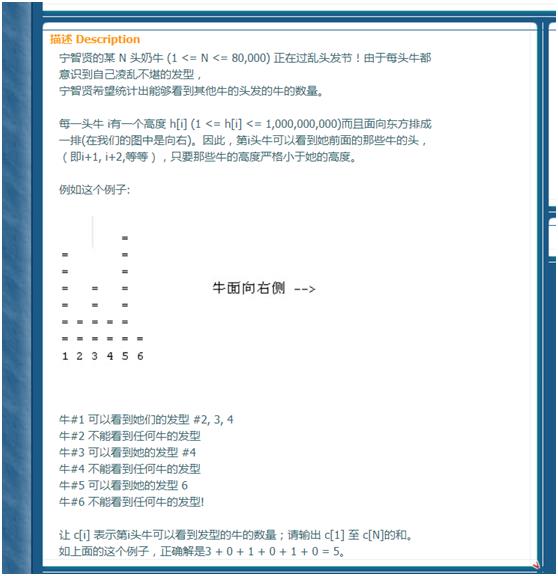
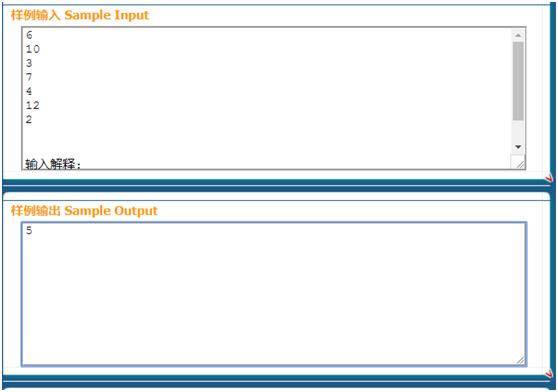
作为我校校本教材题目…教育价值大于题目价值系列
单调栈,就是具有单调性的栈,单调递增或是单调递减。
以上面那道奶牛题距离,最基本最暴力的解法就是二重循环枚举统计,但是N(1<=N<=80,000)的范围二重枚举肯定会超,所以显然暴力枚举是不行了。但是我们如果仔细思考一下就会发现,对于符合条件的情况来看,牛的高度是单调的,一旦h[i+1]>=h[i],就不符合条件了。采用逆向思维,对于第i头牛来说,如果它是第一个比第k头牛高的,那么第k头牛能看到的牛的距离就是i-k-1头(不要问我为什么要减一,第k头牛看不到自己的头)。
比如6头牛,高度分别是:10,3,7,4,12,2。第5头牛高度12,那么第4头就被第5头的高度维护掉了,第三头就只能看到1头,第一头能看到三头,而第二头被第三头的高度维护掉了。我们要做的是用栈维护牛与牛之间单调递减的局部关系。
1) 如果当前元素大于栈顶元素,栈顶出栈,统计栈顶看见了几头牛。
2) 如果栈为空,或当前元素比栈顶小,当前元素进栈。
因为操作只有当前元素进一次栈出一次栈,所以复杂度是O(n)。
代码如下:
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <ctime>
#include <cmath>
using namespace std;
const int maxx=1000090;
int stack[maxx],a[maxx],top=0,n,t;
long long gg=0;//gg为统计的奶牛能看到的头数.
inline void push(int x)//进栈
{stack[++top]=x;}
inline int pop()//出栈
{return stack[top--];}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i];
push(1);
for(int i=2;i<=n;i++)
{
while((a[stack[top]]<=a[i])&&(top>0))
{
t=pop();
gg+=i-t-1;
}
push(i);
}
while(top>0)//处理最高的那个奶牛,若最高的奶牛不是最后一头,就要解决最高的那头所看到的奶牛数。
{
t=pop();
gg+=n-t;
}
cout<<gg<<endl;
return 0;
}
然后还有另一个思路,但是因为我校评测机的问题,不能A掉,但实际输出与测试数据是符合的,很迷,比较尬的是,我校校本教材上给出的这个思路的代码不仅会CE,而且程序连样例的过不去,WA声一片,所以进行了修改。其思路在于,先读入第一个元素,然后按照正常的方式向后找,注意:for循环为for(int i=1;i<n;i++),但如果有比第一个元素还大的高度,就将栈清空,将当前元素入栈,再进行搜索,而且很重要的是,top的大小就是在这一时刻此前所有的能看到当前奶牛的总和,例如:6 5 3 2 8。比如第3头牛高度为3,前两头都能看见,此时top=2,则ans+=top就是ans+=2。第4头牛前三头都能看到,top=3,ans+=top就是ans+=3。
代码如下:
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cstring>
#include <ctime>
#include <cmath>
#include <algorithm>
using namespace std;
const int maxx=100000;
int s[maxx],m,n,top=0;
long long ans=0,f=1;
inline void push(int m)
{s[++top]=m;}
inline int pop()
{return s[top--];}
int main()
{
cin>>n;
cin>>m;
push(m);
for(int i=1;i<n;i++)
{
cin>>m;
if((s[top]<=m)&&(top>0))
{
pop();
if(s[1]<=m)//如果有比栈中第一个元素要大的,将栈清空,当前元素继续向下搜索
f=0;
}
if(f==0)//接上
{top=0;}
else
ans+=top;//top的大小就是之前的牛能看到的牛的总和
push(m);
f=1;
}
cout<<ans<<endl;
return 0;
}
然后大概到这里,栈得学习就结束了系列
以上是关于OJ1147括号匹配加强版(栈)的主要内容,如果未能解决你的问题,请参考以下文章