针孔成像模型
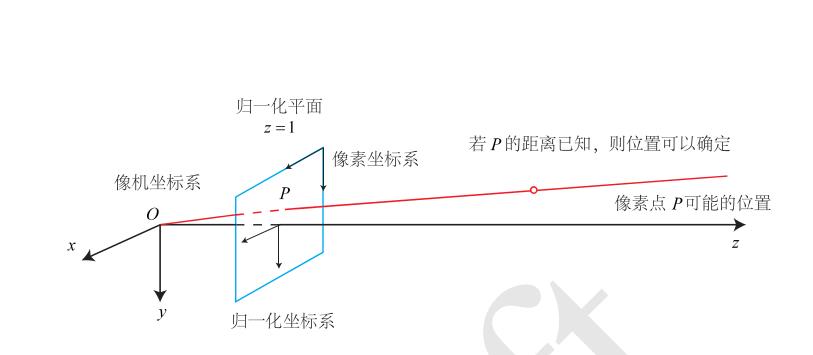
假设OP在z轴上的投影长度为Z, 相机坐标系到像素坐标系的长度为f(焦距)， P在世界坐标系的坐标为(X,Y,Z), 像素为x, 则：
\\[\\frac{x} { f} =\\frac{ X}{Z}
\\]
实际上，芯片的中心通常不在光轴上，我们需要引入两个参数$c_x$和$c_y$对可能的偏移建模，这样现实世界中的点Q,其坐标为(X, Y ,Z) ,以某些偏移的方式投影为点($X_screen$,$y_screen$) ， ：
\\[x_{screen} = f_x(\\frac{X}{Z}) + c_x, y_{screen} = f_y(\\frac{Y}{Z}) + c_y
\\]
注意我们引入了两个不同的焦距。原因是单个像素点在低价的成像仪上是矩形不是正方形。焦距\\(f_x\\)实际上是透镜的物理焦距长度与成像仪每个单元尺寸\\(s_x\\)的乘机（这样做的意义是在\\(S_x\\)单位是像素/每毫米， 而F 的单位是毫米，这以为着\\(f_y\\)的单位是像素）。
整理成矩阵形式：
\\[q = MQ, 其中q=\\left(\\begin{array}{ccc} x \\\\ y \\\\ z \\end{array} \\right), M = \\begin{bmatrix}f_x & 0 & c_x \\\\ 0 & f_y & c_y \\\\ 0 & 0 & 1 \\end{bmatrix},Q=\\left(\\begin{array}{ccc} X \\\\ Y \\\\ Z \\end{array} \\right)
\\]
展开上公式，可以发现$$Z=w $$,点q 是齐次坐标系。
对齐理论推导
设彩色相机的像素 \\(p_{rgb}=\\begin{bmatrix}u_{rgb}\\\\v_{rgb}\\\\1\\end{bmatrix}\\)（齐次），基于彩色相机坐标系下的空间点\\(P=\\begin{bmatrix}X\\\\Y\\\\Z\\end{bmatrix}\\), 设内参为：
\\[K_{rgb}=\\begin{bmatrix} f_{x-rgb} & 0 & c_{x-rgb} \\\\ 0 & f_{y-rgb} & c_{y-rgb} \\\\ 0 & 0 & 1 \\end{bmatrix}
\\]
则有：
\\[z_{rgb}*p_{rgb}=K_{rgb} \\times P_{rgb}
\\]
同理：
\\[z_{ir}*p_{ir}=K_{ir} \\times P_{ir}
\\]
针对同一个棋盘格，彩色相机的外参： \\(R_{CO}\\)与\\(T_{CO}\\), 深度相机的外参：$R_{DO} \\(与\\)T_{DO}$
两者的关系如下：
\\[R_{CD} = R_{CO}\\times R^{-1}_{DO}
\\]
\\[T_{CD} = T_{CO} - R_{CD} \\times T_{DO}
\\]
对于非齐次坐标系下表示的格各自相机坐标系下的三维点\\(p_{rgb}\\)与\\(p_{ir}\\):
\\[p_{rgb}=R_{CD} \\times R_{DO} + T_{CD}
\\]
综上， $$z_{rgb}*p_{rgb}=K_{rgb} \\times R_{CD}\\times K^{-1}{ir} * z{ir} * p_{ir} + k_{rgb} \\times T_{CD}$$
这样，\\(P_{rgb}\\)与\\(P_{ir}\\)就联系起来了。
为了简化表示，我们令：
\\[R = K_{rgb} \\times R_{CD} \\times K^{-1}_{ir}
\\]
\\[T = K_{rgb} \\times T_{CD}
\\]
则有：
\\[z_{rgb} * p_{rgb} = R \\times z_{ir} * p_{ir} + T
\\]
根据针孔成像模型的\\(Z = w\\), \\(z_{rgb} = z_{ir}\\)