算法导论读书笔记-第十三章-红黑树
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法导论读书笔记-第十三章-红黑树相关的知识,希望对你有一定的参考价值。
算法导论第13章 红黑树
红黑树(red-black tree)是许多平衡搜索树中的一种, 可以保证在最坏情况下基本动态集合操作的时间复杂度为O(lgn).
13.1 红黑树的性质
红黑树(red-black tree) : 满足下面性质的二叉搜索树:
- 每个结点是红色的或者黑色的.
- 根结点是黑色的.
- 叶结点都是黑色的.
- 红色结点的子节点都是黑色的.
- 对每个结点, 从该结点到其所有后代叶结点上, 均包含相同数目的黑色结点.
叶结点不存储关键字.
黑高(black-height) : 性质5定义了黑高的概念. 从结点\\(x\\) 出发(不含该结点), 到达一个叶结点的任意一条简单路径上的黑色结点个数称为该结点的黑高, 记为\\(bh(x)\\) .
引理13.1 : 一棵有\\(n\\) 个内部结点的红黑树的高度至多为\\(2lg(n+1)\\) .
由引理易得, 动态集合操作SEARCH, MINIMUM, MAXIMUM, SUCCESSOR, PREDECESSOR可在红黑树上在O(lgn)时间内执行.
13.2 旋转
如果直接用二叉搜索树的INSERT和DELETE操作作用在红黑树上, 运行时间固然为O(lgn), 但由于对树做了修改, 可能导致操作后的树不再满足红黑性质, 因此还需要维护这些性质的操作. 操作分为两部分, 一部分是维护指针, 另一部分是维护颜色. 而维护指针的工作由旋转(rotation)完成.
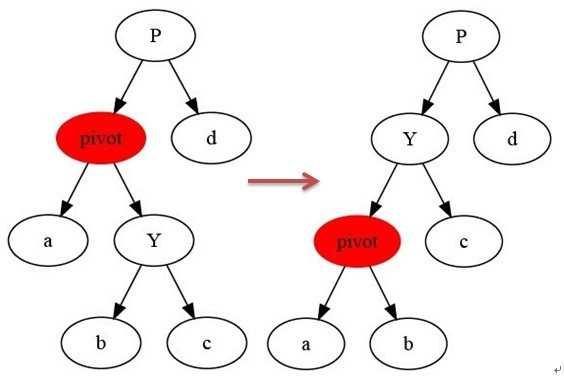
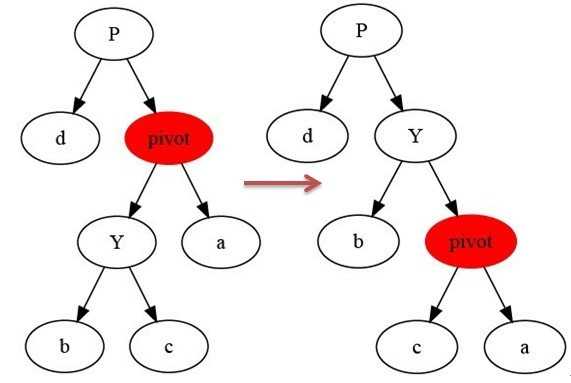
# 在树T中,以x结点为轴进行左旋转操作
# 这里将所有叶子结点以及根结点的父结点,都用哨兵T.nil表示
# 假设x右子树不为空, 即x.right!=T.nil
left_rotation(T,x):
y = x.right
# y的左子树变成x的右子树
x.right = y.left
if y.left != T.nil:
y.left.p = x
# 用y代替x的位置
y.p = x.p
if x.p == T.nil:
T.root = y
else if x == x.p.left:
x.p.left = y
else:
x.p.right = y
# x变成y的左子树
y.left = x
x.p = y# 在树T中,以x结点为轴进行右旋转操作
# 这里将所有叶子结点以及根结点的父结点,都用哨兵T.nil表示
# 假设x左子树不为空, 即x.left!=T.nil
right_rotation(T,x):
y = x.left
# y的右子树变成x的左子树
x.left = y.right
if y.right != T.nil:
y.right.p = x
# 用y代替x的位置
y.p = x.p
if x.p == T.nil:
T.root = y
else if x == x.p.left:
x.p.left = y
else:
x.p.right = y
# x变成y的右子树
y.right = x
x.p = y13.3 插入
# 在红黑树T中插入结点z
# 先将T当作普通二分检索树插入结点z,并将z置为红色
# 再调用辅助程序rb_insert_fixup对结点进行重新着色并旋转
rb_insert(T,z):
y = T.nil
x = T.root
# 前一部分与二分检索树的插入一样
while x != T.nil:
y = x
if z.key < x.key:
x = x.left
else:
x = x.right
z.p = y
if y == T.nil:
T.root = z
else if z.key < y.key:
y.left = z
else:
y.right = z
# 以下是保持树结构的操作
z.left = T.nil
z.right = T.nil
z.color = RED
rb_insert_fixup(T,z)rb_insert_fixup(T,z):
while z.p.color == RED:
if z.p == z.p.p.left:
y = z.p.p.right
# 情况1: z的叔结点是红色
if y.color == RED:
z.p.color = BLACK
y.color = BLACK
z.p.p.color = RED
z = z.p.p
# 情况2: z的叔结点是黑色的且z是一个右孩子
# 转化成情况3
else if z == z.p.right:
z = z.p
left_rotate(T,z)
# 情况3: z的叔结点是黑色的且z是一个左孩子
z.p.color = BLACK
z.p.p.color = RED
right_rotate(T,z.p.p)
else:
# 与前面对称,即左右互换
T.root.color = BLACK对 rb_insert_fixup 所要做的操作进行分析: 插入这个红色结点只可能破坏性质2(如果插入为根结点)和性质4(如果插入后父结点为红色).
对rb_insert_fixup中的while循环进行分析: 每次循环分为三种情况, 情况1将z在T中的位置上升两层, 而情况2和3执行后将退出循环, 因此该操作为O(h)即O(lgn)的.
- 对情况1, z的叔结点是红色, 首先注意z的祖父结点一定是黑色, 因为插入之前的红黑树是满足红黑性质的, 而此时需要解决的是z和z的父结点都是红色. 那么现在z的父,祖父,叔结点是红黑红的情况, 只需要变成黑红黑, 就解决了之前的局部问题, 现在只是把问题向上传递了, 因为z的祖父变成红色, 它的父结点可能也是红色. 此时把z的父结点赋给z, 进行新的循环.
- 对情况2, z的叔结点是黑色, 且z是一个右孩子, 为方便处理, 可以直接转为情况3, 具体做法是以z的父结点为轴做一次左旋转.
- 对情况3, z的树结点是黑色, 且z是一个左孩子, 现在z, z的父结点, z的祖父结点是红红黑, 且全是左孩子关系, 矛盾在于两个红色结点的父子关系违背了红黑性质, 解决的基本想法是把一个红色结点移到祖父结点的右子树上, 通过一个以祖父结点为轴的右旋转操作, 然后把颜色变成红黑红, 就解决了之前的局部问题. 而且我们并没有引入任何新的性质破坏, 因为相比情况1, 现在的轴的颜色是黑色. 因此循环应该在下一次终止了.
13.4 删除
# 将红黑树中的结点u用v代替
# 与二分检索树中的transplant并不逻辑上的不同
br_transplant(t,u,v):
if u.p == T.nil:
T.root = v
else if u == u.p.left:
u.p.left = v
else:
u.p.right = v
v.p = u.p# 从红黑树T种删除结点z
# 基本结构与二分检索树的差不多
# 如果要删除的结点是黑色的,有可能破坏红黑性质
# 调用辅助程序rb_delete_fixup
rb_delete(T,z):
y = z
y_original_color = y.color
if z.left == T.nil:
x = z.right
rb_transplant(T,z,z.right)
else if z.right == T.nil:
x = z.left
rb_transplant(T,z,z.left)
else:
y = tree_minimum(z.right)
y_original_color = y.color
x = y.right
if y.p == z:
x.p = y
else:
rb_transplant(T,z,y)
y.right = z.right
y.right.p = y
rb_transplant(T,z,y)
y.left = z.left
y.left.p = y
y.color = z.color
if y_original_color == BLACK:
rb_delete_fixup(T,x)rb_delete_fixup(T,x):
while x != T.root and x.color == BLACK:
if x == x.p.left:
w = x.p.right # x的兄弟结点
# 情况1: x的兄弟结点是红色
if w.color == RED:
w.color = BLACK
x.p.color = RED
left_rotate(T,x,p)
w = x.p.right
# 情况2: x的兄弟结点是黑色,并且x的两个侄子结点都是黑色
if w.left.color == BLACK and w.right.color == BLACK:
w.color = RED
x = x.p
# 情况3: x的兄弟结点是黑色,并且x的左侄子是红色,右侄子是黑色
else if w.right.color == BLACK:
w.left.color = BLACK
w.color = RED
right_rotate(T,w)
w = x.p.right
# 情况4: x的兄弟结点是黑色,并且x的右侄子是红色
w.color = x.p.color
x.p.color = BLACK
w.right.color = BLACK
left_rotate(T,x.p)
x = T.root
else:
# 与上面类似,左右互换
x.color = BLACKrb_delete_fixup的基本思路: 如果在rb_delete中被删除的结点y是黑色结点, 新代替的结点为x, 会带来如下问题: 若y是原来的根结点, 而x是红色结点, 违反性质2; 若x和x.p都为红色结点, 违反性质4; 在树中移动y将导致先前包含y的简单路径上黑结点个数少1, y的任何祖先都不满足性质5.改正思路是将x视为还有一重额外的黑色. 在这种假设下, 性质5成立. 而问题变为, x为双重黑色或红黑色, 违反性质1.
rb_delete_fixup中的while循环做这样一件事情, 将额外的一层黑色沿树上移或在循环某一步中消除. x是一个不断(沿树上升的方向)变化的量, x所指的结点表示"多一层黑色". 循环在下面几种情况终止:
- x指向红黑结点, 即color域本身是RED的结点, 此时直接把红色去掉, 即颜色变成黑色即可.
- x指向根结点, 此时简单移除额外黑色即可.
- 执行适当的旋转和重新着色, 退出循环.
while循环处理以下四种情况:
x的兄弟结点w是红色的, 此时通过旋转操作转换成2,3,4处理, 即把兄弟结点换一个黑色结点.
x的兄弟结点w是黑色的, 而且w的两个子结点都是黑色, 说明w换成红色不影响性质4, 此时把w变成红色, 即将x的额外一层黑色和w的黑色同时脱去, 给它们的父结点, 不影响性质5. 这样就让额外的黑色往上走了一层, 把x同样跟踪上去, 进入下一个循环.
注意, 如果由情况1进入情况2, 此时父结点一定是本来是红色结点, 即变换后的x是红黑结点, 下一步可以退出循环.
x的兄弟结点w是黑色的, 而且w的左孩子是红色, 右孩子是黑色, 此时通过旋转变色直接转换成情况4.
x的兄弟结点w是黑色的, 而且w的右孩子是红色, 此时不管x和w共同的父结点是什么颜色, 不妨设为C, 那么[x, x的父结点, w, w的右孩子] 此时是黑X黑红, 通过将父结点和w颜色交换, w的右孩子变成黑色, 然后以父结点为轴进行左旋, 可以将x的额外黑色脱给w原来的右孩子, 依然保证性质5成立, 循环可以结束.
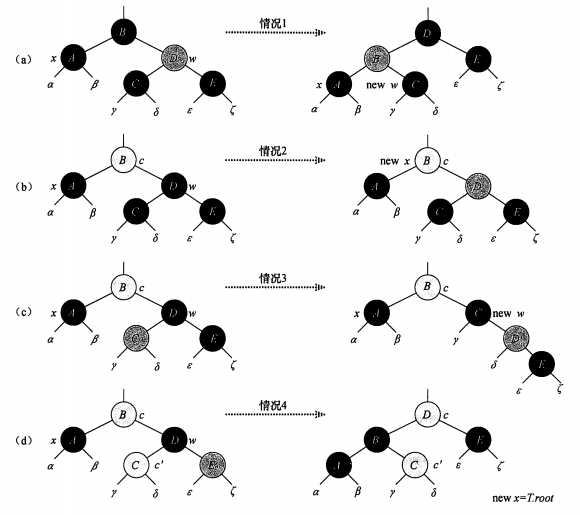
由以上分析容易知道, rb_delete的运行时间为O(h)即O(lgn).
以上是关于算法导论读书笔记-第十三章-红黑树的主要内容,如果未能解决你的问题,请参考以下文章