51nod 1021 石子归并 （动态规划 简单代码）

Posted 2020-10-14

题目：

 

 

 

思路：动态规划，递推式子 dp[i][j] = min(dp[i][j], dp[i][k] + dp[k+1][j] + sum[j] - sum[i-1]);

　　    dp[i][j]表示合并第i到第j个石子需要的最少代价。sum[i]表示前i个石子的价值，sum[j] - sum[i-1]即合成两堆石子（（第i到第k合并出的石子），（第k+1到第j合并出的石子））。

　　　

 

但是考虑要求1-4，

需要先求出（1-1，2-4），（1-2,3-4），（1-3,4-4）。

所以我们不能直接按横纵坐标遍历。

需要换一种遍历方式，在纸上画一画就可以知道有哪些可行的遍历方式了。

 

 

我的遍历方式是

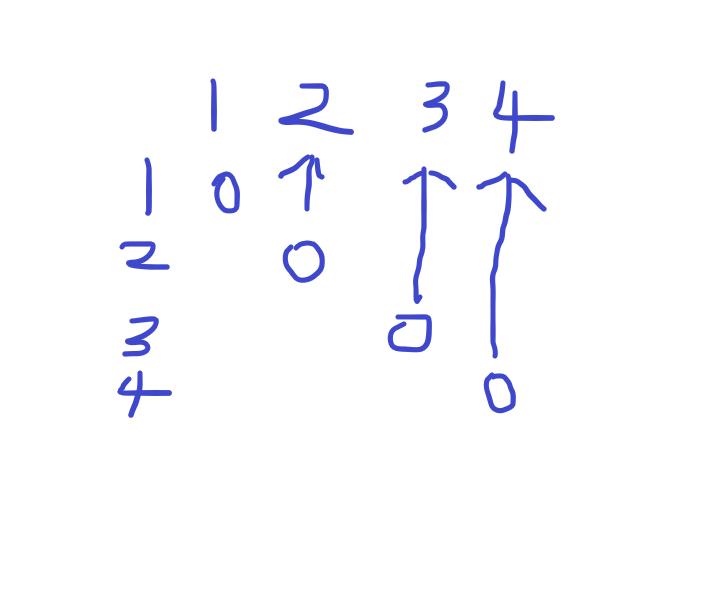
从左往右看，对角线全是0，表示合并(i,i)的代价是0。

 

这种遍历方式能够保证遍历是按照逻辑上的顺序的。

 

 

 

代码：

#include <iostream>
using namespace std;
typedef long long ll;
#define INF 2147483647

//输入 
int n;
int a[110];            

int dp[110][110];//dp[i][j]表示第i到第j堆石子合成所需的最小代价   
int sum[110];    //前缀和 

int main(){
    cin >> n;
    for(int i = 1;i <= n; i++) cin >> a[i], sum[i] = sum[i-1] + a[i];
    int ans = 0;
    
    for(int i = 1;i <= n-1; i++){
        //（x，y）表示图上每一个箭头的起点 
        int x = i;int y = i+1;
        //开始往上走（箭头方向）        
        while(x >= 1){
            dp[x][y] = 2000000000;
            
            for(int j = x;j <= y-1; j++){
                dp[x][y] = min(dp[x][y],dp[x][j] + dp[j+1][y] + sum[y] - sum[x-1]);
            }
            x--;
        }
    }
    cout << dp[1][n] << endl;
    return 0;
}